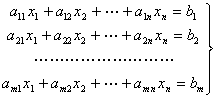2.4.3.2　線形計画法のシンプレックス法　　　　　　目次（第２章）へ

　変数の数，制約条件式の数が多くなると図式解法は不可能となり，以下に述べるシンプレックス法を導入し解を求める．

　（2.78）〜（2.80）式の不等式は，非負のスラック変数（slack variable）を導入して等式に書き変える．

　　　x₁ + x₂ + x₃ = 10　　　　　　　　　　　　　 　　　　 eq. 2.82

　　　2x₁ + x₂ + x₄ = 16　　　　　　　　　　　　 　　　　　eq. 2.83

　　　x₁ + 3x₂ + x₅ = 24　　　　　　　　　　　　 　　　　　eq. 2.84

　また，ここでは目的関数を最小にする演算方式に合わせるために，符号を変えて，

　　　z =−3x₁−2x₂　　　　　　　　　　　　　　 　　　　eq. 2.85

で表されるzを最小にすることを目的とする．一般式で示すと，

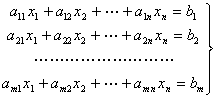　　　　　　　 　　　　　　　eq. 2.86

の制約条件で

　z = c₁ x₁ + c₂ x₂ + … + c_n x_n　　　　　　　　　　　　　　eq. 2.87

を最小にすることを目的とする．例題では，m = 3，n = 5であり，図式解法の頂点に対応する可能基底解は，表2.6で示される．

●ソフトウェア　LP.exe

表2.6　可能基底解

　そこで，原点Oの可能基底解から，つぎのようなシンプレックス表を順次計算して最適解を求める．

　ここで，P₁ =（a₁₁，a₂₁ … a_m1），P_j =（a_{1 j}，a_{2 j} … a_{m j} ），P₀ =（b₁，b₂ … b_m ）である．

また，P₃，P₄，P₅は基底ベクトルとよばれる（表2.7）．

表2.7　シンプレックス表（0点）

スラック変数x₃，x₄，x₅は，（2.86）式より

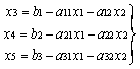　　　　　　　　　　　　 　　eq. 2.88

（2.88）式を（2.87）式に代入すると，

　　z = c₁ x₁ + c₂ x₂ + c₃（b₁−a₁₁ x₁−a₁₂ x₂）+ c₄（b₂−a₂₁ x₁−a₂₂ x₂）

　　　+ c₅（b₃−a₃₁ x₃−a₃₂ x₂）

　　　=［c₃ b₁ + c₄ b₂ + c₅ b₃］−［（c₃ a₁₁ c₄ a₂₁ + c₅ a₃₁）−c ₁］x ₁

　　　−［（c₃ a₁₂ + c₄ a₂₂ c ₅ a₃₂］−c₂］x₂

　　　= z ₀−（z₁−c₁）x₁−（z₂−c₂）x₂　　　　　　　　eq. 2.89

ただし，z ₀ = c₃ b₁ + c₄ b₂ + c₅ b₃，z₁ = c₃ a₁₁ + c₄ a₂₁ + c₅ a₃₁，z₂ = c₃ a₁₂ + c₄ a₂₂ + c₅ a₃₂ である［z _j = Σc _i a _{i j}（i行j列）］．

したがって，x₁ = x₂ = 0の原点では目的関数はz ₀となり，（z₁−c₁）あるいは（z₂−c₂）が正であれば，x ₁，x ₂の増加によって目的関数zをさらに小さくすることができる．

　z _j−c _jが最大であるj = 1から，x₁を増加させることにするが，x₁の増大には限度があり，x₃，x₄，x₅ は非負，かつ（2.88）式から，

　　x₁ ≦ b₁ / a₁₁ = θ₁　　　　　　　　　　　　　　　　　　eq. 2.90

　　x₁ ≦ b₂ / a₂₁ = θ₂　　　　　　　　　　　　　　 　　　　eq. 2.91

　　x₁ ≦ b₃ / a₃₁ = θ₃　　　　　　　　　　　　　　 　　　　eq. 2.92

のいずれも満足する必要があり，θ_iの最小値よりも大きくはできない．

表2.7の例では，θ₁ = 10/1，θ₂ = 16/2，θ₃ = 24/1であり，θ₂が最小値8となり，（2.88）式からx ₄ = 0となり，D点に移ることになる．すなわち，表2.7の＊印の要素をピボットとして，P₄ベクトルをP₁ベクトル（新しい基底ベクトル）に入れかえる．ピボットa_ιk（ι=，k = 1）= 2から，新しいシンプレックス表は，

b_l'= b_l / a_lk = 16/2から

b_i'= 8, b_i'= b_l - b_l・a_ik / a_lk = (i=1,3) から，

b₁'= 10 - 16・1/2 = 2, b₃'= 24 - 16・1/2 = 16,また，a_lj' = a_lj / a_lk から

表2.8　シンプレックス表（Ｄ点）

a_2j' = a_2j / 2, a_ij'= = a_ij - a_lj・a_ik / a_lk (j=1,3)からa_1j' = a_1j - a_2j・1/2, a_3j' = a_3j - a_2j・1/2から表2.8は得られる.

　同様にして，x ₃ = x ₄ = 0のC点へ移るべく，P₃ベクトルをP₂ベクトルに入れかえて表2.9が得られる（ι= 1，k = 2）．

表2.9　シンプレックス表（Ｃ点）

　表2.9では，いずれのz _j−c _j も正でなく，z =−26が最小値となっていることを示す．

　また，x₃，x₄の潜在価格（z₃−c₃，z₄−c₄）が−1であることは，耕地面積を1ha，または労力を100人h／ha増加させると，最大粗収益が100万円上がって，2,700万円になることを意味する．あわせて，P₀列の値は，x₂ = 4，x₁ = 6が解を示し，x₅ = 6は，6（×100kg）の肥料が余ることも示している．

　JIS（Z8121）によると潜在価格（shadow price）とは，「最適解に対する評価ベクトルで，制約式の右辺の定数の値を１単位増加したときの目的関数の値の変化を示す」ものである．

次章 2.4.4 スケジューリング　へ