2.4.3 線形計画法 目次(第2章)へ
あるシステムの制約条件式と評価関数がともに線形の数式で表されるときは,そのシステムの最適解は解析的に求められ,その手法を線形計画法 (Linear Programming)とよぶ.
〔例題〕 ある農家の耕地面積は10haで,作物A,Bを栽培するとき,年間労力はAでは200人/ha,Bでは100人/haかかり,肥料はAでは100kg/ha,Bでは300kg/ha必要とし,売上高はAが300万円/ha,Bが200万円/haであるとき,粗収益zを最大にする作物A,Bの栽培面積(x1 x2)を求めよ.ただし年間労力は1,600人h,年間肥料使用量は2,400kgまで供給可能とする.
〔解〕 題意を表示すると表2.5のようになる.
表2.5 営農条件と粗収益
所 要 量 A B |
供給可能量 | |
| 耕地面積(ha) 労力(人h/ha) 肥料(Kg/ha) |
x1
x2 200 100 100 300 |
10 1,600 2,400 |
| 粗収益(万円/ha) | 300 200 |
制約条件式はつぎのように求められる.
x1 + x2 ≦ 10(ha) eq. 2.78
2x1 + x2 ≦ 16(×100人h / ha) eq. 2.79
x1 + 3x2 ≦ 24(×100kg / ha) eq. 2.80
目的関数は,粗収益を百万円の単位で表すと
z = 3x1 + 2x2(×百万円) eq. 2.81
したがって,(2.78)〜(2.80)式の制約のもとで(2.81)式を最大にするx1,x2を求める問題として数式化することができる.
2.4.3.1 線形計画法の図式解法
変数が3以下の場合は,図式解法によって最適解x1,x2,zを求めることができる.

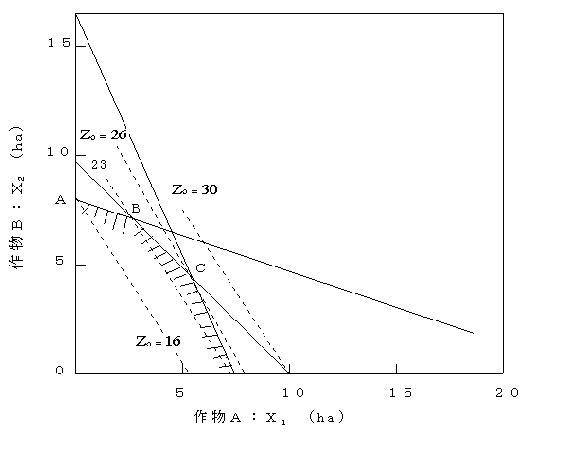
図2.16 線形計画法
図2.16において,制約条件式を同時に満足する領域は,3直線の下側とx1,x2軸で囲まれる凸五角形OABCDの部分である.一方,点線は目的関数を定数z 0としたときの直線群(z 0 = 3x1 + 2x2)を示し,互いに平行で右側へいくほどその値は大きくなる.したがって,点C(x1 = 6, x2 = 4)において,zは最大値26を示すことがわかる.
一般に制約条件式は凸多面体となり,その頂点で目的関数(超平面)が最大あるいは最小になることが知られている.
したがって,頂点ABCDを求め,それらの点における目的関数の値を比較しても最適解が得られる.この場合は,A(0,8),B(3,7),C(6,4),D(8,0)で,z A =16,z B = 23,z C = 26,z D = 24となる.
作物Aを6ha,作物Bを4ha栽培するとき,粗収益は2,600万円と最大になる.
また,C点を規制しているのは,(2.78),(2.79)式であり,耕地面積と労力が粗収益を規制していることがわかる.したがって,耕地面積あるいは労力の供給を増加すれば粗収益はさらに増大する.また,C点では(2.80)式の左辺が18となり,肥料は600kg余ることがわかる.
☆apx.253a 凸集合,端点,最適値