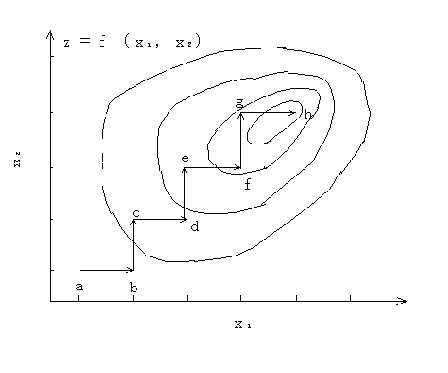
2.4.2.4　整数型最大傾斜法　　　　　　　　　目次（第２章）へ

　次章のような農作業計画で，機械の台数（整数）の組合せを変えて最適化をはかる場合，機械の作業能率についてみるとその値は連続的に変わるのではなくて離散的な値を示している．

このようにあるシステムz =（x₁，x₂，…，x_n）において，その要素x _iが整数（離散値）であるときその目的関数zを最大にすることを考えると，図2.14のようにある点a（x₁₁，x₂₁，…，x_n1）から出発して，傾斜ベクトル▽f（x₁，x₂，…，x_n）の正の方向の点a ₁（x₁₁±1，x₂₁，…，x_n1），点a ₂（x₁₁，x₂₁±1，…，x_n1），…，点a _n（x₁₁，x₂₁，…，x_n1±1）のzの値を求め，そのなかで最大値を示す点a _i（図2.14ではb）をめざす．

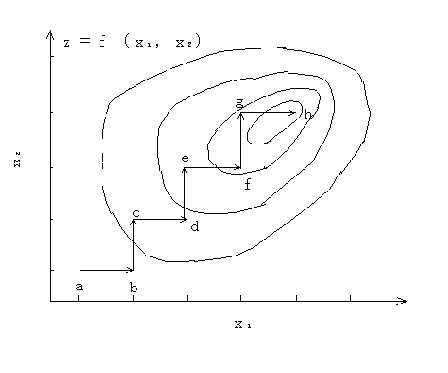
　　　　図2.14　整数型最大傾斜法　　　　　　図2.15　整数型山登りシンプレックス法

　同様にして，

f（c）= max [f（b₁），f（b₂），…，f（b_n）]

となる点cをめざす．

ここで，b =（x₁₂，x₂₂，…，x_n2）　　　 b₂ =（x₁₂，x₂₂±1，…，x_n2）

　　　 b₁ =（x₁₂±1，x₂₂，…，x_n2）　　b_n =（x₁₂，x₂₂，…，x_n2±1）

　このようにして，点d，e，f，…，hと進み，どの方向に向かっても目的関数zが改善されないとき，その値が最適値と考えられる．このような方法を整数型最大傾斜法とよぶことにする．

　なお，制約条件，g（x₁，x₂，…，x_n）≦ 0がある場合は，傾斜ベクトル（▽f）の制約条件境界線 [ g（x₁，x₂，…，x_n）= 0 ]への射影ベクトルの方向で，かつ制約領域内の点をめざして移動して，目的関数の改善の試みを繰り返す．

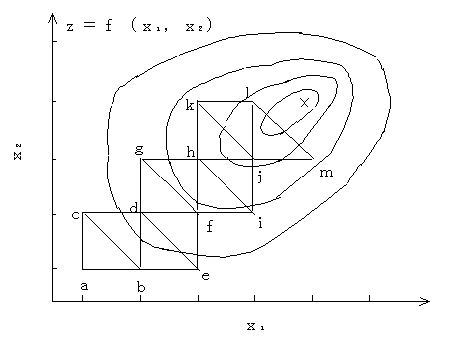
また，山登りシンプレックス法に離散型数値を用いた整数型山登りシンプレックス法を説明しよう．図2.15において３点a（a₁，a₂），b（b₁，b₂），c（c₁，c₂）の値f（a）が最小であるとき，三角形abcの辺bcの反対側の点d（d₁，d₂）をめざす．この例ではd₁= b₁，d₂= c₂である．同様にして，点e，f，g，h，…と移って最適値を求める方法であるが整数型最大傾斜法より劣る．

次章 2.4.3 線形計画法　へ