2.4.2.3 山登りシンプレックス法 目次(第2章)へ
システムの目的関数が2〜3個の変数で表される問題では,山登りシンプレックス法(simplex method:線形計画法のシンプレックス法とはまったく別の方法であるので区別するために山登りを前につけた)とよばれる平易な方法がある .
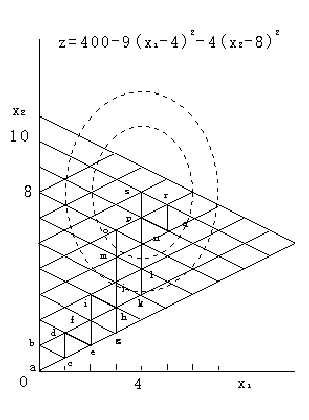
z = f(x1,x2)では,図2.13のように正三角形abcを出発点とし,z = f(x1,x2,x3)では,ある正四面体abcdを出発点として最適値を模索する.

図2.13 山登りシンプレックス法
●ソフトウェア hill_800.exe
図2.13で,zの最大値を求める場合について述べると,まず,
z1 = min[z(a),z(b),z(c)] eq. 2.76
を求め,z1 = z(a)であれば,直線bcに関する点aの対称点dを求める.つぎに,
z2 = min[z(b),z(c),z(d)] eq. 2.77
を求め,z2 = z(b)であれば,直線cdに関する点bの対称点eを求め,同様に,f,g,h…と進め,最終的に最適値z(s)が求まる.
実際には,三角形の形状(正三角形や正四面体でなくてもよい)やその大きさによって最適値の探索効率は大きく影響される.一般には,はじめに大きめの三角形で概略の最適値を探し,その後三角形を小さくとり正確な値を求める.