2.4.2.2 大ステップ傾斜法 目次(第2章)へ
前節に述べたような最大傾斜を与える方法に進むときに,その進み方のステップ幅を前節のように小さくとらず,制約領域をこえない範囲で,また目的関数の値を改善するかぎりでできるだけ大きくえらぶ方法である.
目的関数も制約条件もともに線形方程式f(x)= c1 x1 + c2 x2 + … + cn xnの場合についてこれを説明すると,出発点P0から進むべき方向は▽f(x)= [c1 c2 … cn] = cとなり最大傾斜の方向は常に一定になる.われわれはこのcの方向にできるだけ進み,制約領域の境界面との交叉点P1まで進む.
点P1からはもはやcの方向を進むことはできないから点P1ののっている平面上を▽f(x)= cと最も鋭い鋭角をなす方向に進む.再びこの境界面の限界点P2に達したら再びcと最も鋭い鋭角をなす方向P2,P3の方向に進んでいけばよい.このようにして,もはや制約領域の境界面上では▽f(x)= cと鋭角をなす進路を見出せなくなったときが最適解となる.
以上の方法は目的関数が線形でない場合も適用できるわけで,それにはつぎのようなステップをふめばよい.
①制約条件を満足する任意の点xkにおいて傾斜ベクトル▽f(xk)を計算する.②xkののっている平面のすべてに対して▽f(xk)を投影した方向を求め,xkが制約領域の内部にあるときは▽f(xk)の方向とする.またxkが二つ以上の境界面の交わりの上にあるときではこの二つ以上の境界線上で▽f(xk)と鋭角をなす方向とする.
③ ②の投影成分が0でないときは②で求めた方向に線をのばし,制約領域にとどまっている限界に位置する点をxk+1とする.
1) f(xk+1)<f(xk)なら,再び①にもどる.
2) f(xk+1)≧f(xk)のときはxkxk+1上で最も小さい点を求める.
④ ②の投影成分が0のときはxkが最適解である.
以上述べたような方法は,投影最大傾斜法(projected gradient method)とよばれる.
〔例題〕 2x + y≦8,x≧0,y≧0の制約領域のもとで,目的関数z = 9x2 + 4y2-72x-64yを最小にすることを,図解法および原点を出発とする投影最大傾斜法で求めよ.
〔解〕 目的関数zを変形すると,
z = 9(x-4)2 + 4(y-8)2-400 eq. 2.69
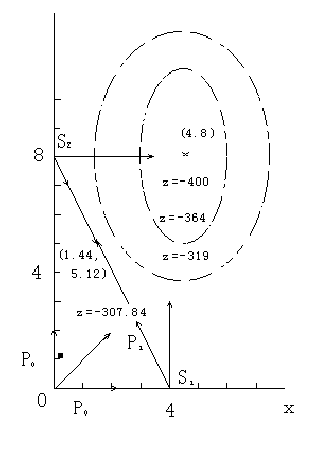
となり,zの等値曲線群は,図2.12のように,点(4,8)を中心に,x方向・y方向の短長軸比2:3のだ円である.なお,zを最小にすることは-zを最大にすることと同じである.
したがって,だ円群の接点を求めるために,制約直線y = 8-2xをzに代入すると
z = 9x2 + 4(8-2x)2-72x-64(8-2x)
=25x2-72x-256 eq. 2.70

図2.12 投影最大傾斜法
●ソフトウェア SGM.exe
また,z’= dz/dx = 50x-72であるから,z’= 0 とおくと,x = 72/50 = 1.44 したがって,y = 256/50 = 5.12であり,最小値zは,z =-307.84となる.
投影最大傾斜法では,まず,
(1) 出発点を原点にとる,S0 =〔0,0〕.この点における傾斜は,
-dz/dx = -18 (x - 4 ) eq. 2.71
-dz/dy = -8 (y - 8 ) eq. 2.72
から,-▽z(S0)=〔72,64〕で,z(S0)= 0
(2)S0は二つの制約境界面x = 0,y = 0の交わりの上にあるから,上の2平面上に,-▽z(S0)を投影して,y = 0の上に投影したときの方向は,P0 =〔72,0〕で,x = 0の上に投影したときの方向は,P0’ =〔0,64〕となる
(3)|P0|>|P0’|であるから,P0の方向に進むとすれば,S1 =〔4,0〕の点で制約領域の境界に達する.ここでは,z(S 1)=-144で明らかに,z(S1)< z(S0)
したがって,再び(1)のステップにもどる.
(1’) S1における傾斜を求めると,
-▽z(S1)=〔0,64〕
(2’) S1は,新たに,2x + y = 8なる境界面に交差することによって生じたものであるから,-▽(S1)のこの面に対する投影を求めると,
P1 = [0・(-4) + (64*8)]/[(-4)2 + (8)2]・[-4, 8]
= [-128/5, 256/5] eq. 2.73
(3’) S1からP1の方向に進むと,つぎの点S2 =〔0,8〕の点で制約領域に達する.ここでは,z S2 =-256で,z(S2)< z(S1),したがって,再び(1)のステップにもどる.
(1”) S2における傾斜は,
-▽z(S2)=〔72,0〕
(2”) この傾斜ベクトルのx = 0なる境界面に対する投影は,0,2x + y = 0なる境界面への投影は,
P2 = [72・(-4) + (0*8)]/[(-4)2 + (8)2]・[-4, 8] = [72/5, -144/5]
=[14.4,-28.8] eq. 2.74
(3”) S2からP2の方向に進むと,S1へもどることになるので,zの最小値は,2x + y = 8,すなわち,y = 8-2x面上にあるので,これをzに代入すれば,
z = 9x2 + 4(8-2x)2-72x-64(8-2x)
=25x2-72x-256 eq. 2.75
これから,dz / dx = 50x-72 = 0として,
x = 36/25 = 1.44
また,y = 128 / 25 = 5.12が得られ,最小値は,z =-307.84である.