2.4.2 最大傾斜法 目次(第2章)へ
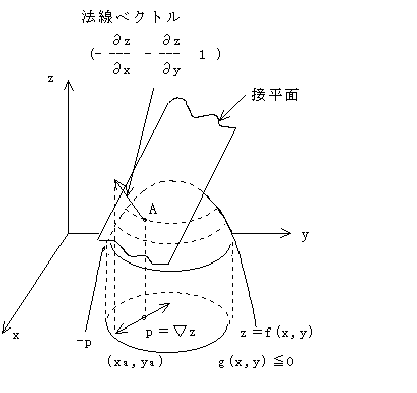
図2.9のように2変数(x,y)に関する目的関数f(x,y)の最大値を制約領域g(x,y)≦0のもとでもとめる問題を考えてみよう.これは制約領域の範囲内で目的関数の山のいちばん高い所に到達することであり,これはちょうど,われわれが山登りをする時の状態によく似ている.頂上に達するいちばんの近道は,できるだけ傾斜の急な所を登っていけばよいわけであるが,このような考えで最適値に達する方法を最大傾斜法(steepest gradient method)もしくは傾斜法とよぶ.

図2.9 目的関数と接平面
任意の一点(x,y)において,目的関数z=f(x,y)に対し,次式で与えられるベクトルpは傾斜ベクトルまたはグラディエントとよばれる.
![]() eq.
2.63
eq.
2.63
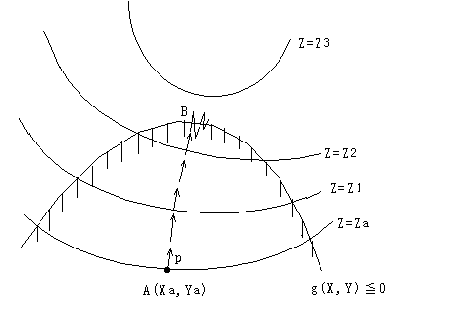
図2.10 傾斜ベクトルにそった目的関数の最適化
このpは図2.10に示すように点Aを通り,目的関数の等高線群に垂直な方向でzの増加する方向に向き,図2.9では斜面の最も急な方向を示している.
また点A(xa,ya)上を通り目的関数f(x,y)の等高線に接する接平面は
z = za + ∂z/∂x ( x - xa)+∂z/∂y ( y - ya) eq. 2.64
で与えられ,もちろん点A(xa,ya,za)を通る.接平面は点Aの近傍でz = f(x,y)を最もよく近似する平面であるから,f(x,y)なる関数を近似しようとするときはこの平面を用いることができる.
2.4.2.1 微分傾斜法
さて,いま図2.10においてわれわれは制約領域内の一点Aにいるものと考えよう.この場合目的関数z = f(x,y)で与えられる斜面をできるだけ早く最適値に達するには傾斜の最も急な方向(傾斜ベクトルの方向)に進んでいけばよいわけであるが制約領域をはみ出してしまうわけにはいかない.そこでなんらかの方法で,新しく到達する点を制約領域の中にとどめておくような処置が必要になる.
この方法としては直接微分傾斜法(direct differential gradient method)とラグランジュの微分傾斜法(Lagrangian differential gradient method)の二つがある.
直接法では図2.10のごとく,たえず自分の位置が制約領域にとどまっているかどうかをしらべ,とどまっていればpの方向にそのまま進み,制約領域をはみ出したとき(たとえば図2.10の点B)はただちに制約領域の境界に直角の方向に逆もどりして,できるだけ早く制約領域内にもどるようにする.これを数式で表すとつぎのようになる.
q=λ・p−δ▽g(x,y) eq. 2.65
ここでq:1回に進む歩み
λ:g(x,y)≦0のとき正の数,g(x,y)>0のとき0
δ:g(x,y)≦0のとき0,g(x,y)>0のとき正の数k eq. 2.66
▽g(x,y)はいうまでもなく制約領域を与える関数g(x,y)に直角な方向を示すものである.またδは制約領域にとどまっていれば0であるが,これをはみ出すと,正の値kがえらばれ,図2.10のように後退する(kick back)ことになる.kはたとえば,境界上における|▽f(x,y)|/|▽g(x,y)|より大きい値にえらんでおけばよいであろう.
このkの値のえらび方や,さらには1回ごとのステップで進むべき歩み|q|の大きさを適当にえらぶ必要がある.たとえばあまり|q|を小さくとれば最適値に到達するまでに何回もの繰返し計算をしなければならないであろうし,あまり大きくえらぶと歩みが粗雑になって,最適値付近で振動してしまうことになる.
直接微分傾斜法では(2.65)式の右辺が制約領域の内・外で不連続的にかわるが,ラグランジュ微分傾斜法では次の(2.67)式のようにしてこの不連続性をなくし,しかもたえず制約条件を考慮することができる.
q =λ・p−u▽g(x,y) eq. 2.67
ここで,u:g(x,y)≦0のときu = 0,
g(x,y)>0のとき,u = g(x,y) eq. 2.68
制約領域を大きくはみ出ると(2.68)式によってg(x,y)も大きな正の値となり,uの値も大きくなり,これが(2.67)式の右辺に反映されて大きく引返す効果をもつ.いいかえればこの方法は,(2.65)式においてδの大きさを制約領域のはみ出し方に比例させたものということができる.またこのようにして得られるxの収束値は制約条件式を満足し,かつ,f(x,y)の最適値を与える.
本手法において注意すべきことは,上に述べた方法は制約条件式も目的関数も凸の場合は必ず最適値に導くが,図2.11の場合のように局部的な最大値(local maximum)に達してしまって真の最適値に達することのできない場合があることである.
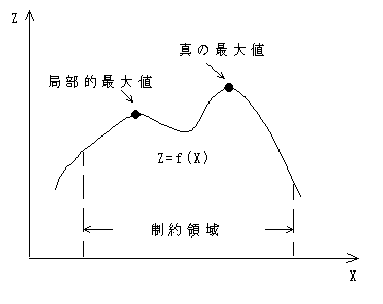
図2.11 局部的最大値と真の最大値