2.4 システムの最適化 目次(第2章)へ
2.4.1 シミュレーション
そのシステムモデルが線形計画法によって作成されていると,解析的計算によって,一義的な解が得られ,1回の計算によって最適化を行うことができようが,通常のシステムモデルは複雑な非線形のモデルであって解析的に最適化を行うことはできない.そこで,そのような場合には,種々の要素・変数を変えてそのシステムモデルの評価関数を求め,そのなかから評価関数の最大値を求める.すなわち最適化を行う.これがシミュレ−ション( Simulation )とよばれるもので,ハ−ドウェアにおける要因実験に対応するものである.
2.4.1.1 シミュレ−ションによる分析と最適化
大規模で複雑なシステムの最適化をはかるには,そのシステムの構造・機能をモデル化し,その入力やパラメータを変化させてシステムの挙動を明らかにしていくシミュレーションの手法が用いられる.
シミュレーションの一般的手順はつぎのとおりである.
1) 目的の明確化:評価関数の設定
2) データの収集・調査
3) モデル化とプログラミング
4) コンピュータ演算
5) 結果の評価と分析
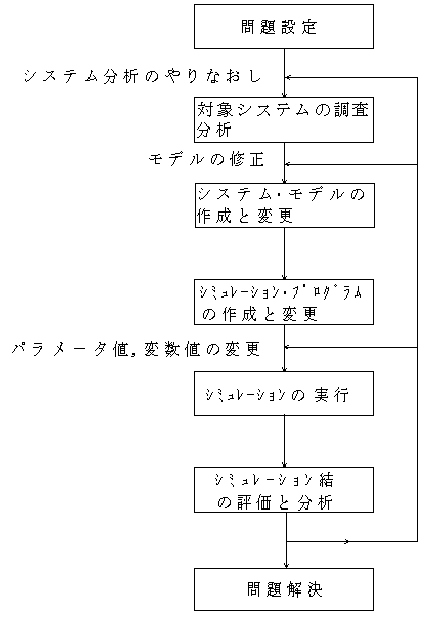
これらの過程をフローチャートで示したのが図2.5である.

図2.5 シミュレーションの過程(BPSE3-1.jbh)
240haの牧草地の収穫作業を,刈取機, テッダー,レーキ,ヘイコン,ベーラー,トレーラ,トラクタ,乾燥機,ヘイプレス,キューバ何台で作業するのが最も経済的であるかという問題では,まず,その収穫作業体系のモデルを作成した.モデルは,時間を軸とした動的モデルで,その作業行程を数式と論理式で表現しFORTRANでプログラミングしたものである.
シミュレーション演算は,そのモデルを使って各種の機械の組合せのもとに数十回行い,その評価関数(利益=生産売上高−経費)を最大にするものを最適解とする.なお,シミュレーション演算は,ハードウェアにおける実験に相当し,実験計画法を適用して行うのが望ましい.
シミュレーションを効率的に行うには,山登り法,最大傾斜法などがあるが次節で述べるように多峯型のシステムでは,最適解を見逃す危険性が高い.そこでシミュレ−ションにおいては,まずそのシステムの全貌を把握する必要があるので,各要素のとりうる値の最大・最小を含む3〜5水準の要素の値に関して,実現可能と思われるあらゆる要素間の組合せについてそのシステムの目的関数を演算することが望ましい.要素の数が少ない場合は,つぎのように実験計画法でいう「完全配備型」演算で行えばよい.
〔例〕 植物の生長モデルにおいて,植物乾物重zが濃度x1、湿度x2、光x3、CO2濃度x4、土壌水分x5の関数で表されているとき,各要素の最大値,最小値,平均値の3水準について全組合せを考えると,3・3・3・3・3=35 =243 通りの演算を行うことによって,各要素と植物乾物重のおよその関係が明らかになる.
しかしながら,農業システムのように要素の数が多くなると、「完全配備型」演算の回数は急激に増大する.たとえば,要素の数10で3水準の値の組合せ は310 = 59049,要素の数15では315 = 14,348,903となり,演算時間が急増する.このような場合には「直交配列表」によっ,て組合せの間引きを行う方法や,ランダムに組合せをとりあげる方法などが用いられる.従来の経験や研究結果から要素間の交互作用がない場合,すなわち相乗効果がないことがわかっている場合には,多元配備型の複式演算計画でなく、単式演算計画でよいこともある。
〔例〕 前例で単式演算を行うときは他の要素はいずれも平均値に設定してそれぞれの要素について3水準に変えて演算を行えばよいから,その演算の回数は1+2n,n = 5のとき11回である.
2.4.1.2 農作業計画への応用
全体の農作業システムは,非常に複雑であるので,簡単な部分システムを対象にして最適化の手法の一事例を以下に説明する.
a) 牧草収穫作業体系
前節でモデル化した牧草収穫作業体系について,そのシステムモデルの解析を行った.入力パラメータとしては,二つの草生長型,各種の機械の台数の組合せを用い,シミュレ−ション演算を行った結果の出力例が図2.6である.
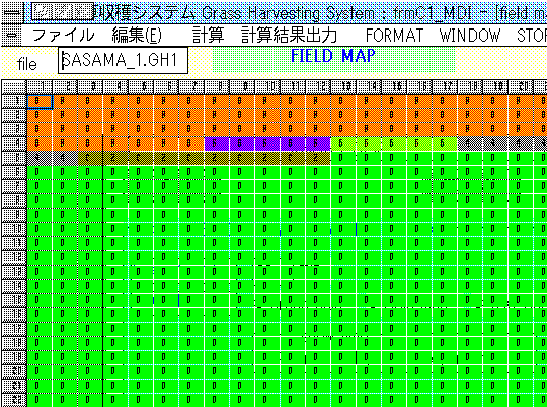
図2.6 圃場マップの例
図2.6は,6月10日午後4時その日の作業の集計を行った例で,圃場マップは各区の作業状況を草の状態コ−ド番号で示し,処理量は各作業別のその日の草量を示し,各作業の稼働状態は機械の番号順に1台ごとのその日の作業時間を示している.
機械の年間稼働時間をまとめた例が図2.7であり,稼働時間の状況をみて機械の台数の増減の可能性を判断し,試行錯誤方式で機械の組合せを変えて解析を行う.

図2.7 機械の稼働時間(BPSE3-3.JBH)
図2.7では,トラクタ15台のうち10台は年間稼働400時間以上であるが,あとの5台の稼働率は小さい.ベ−ラ,トレ−ラについてもあとの数台の稼働率は小さい.そこで,トラクタ13台,テッダ・レ−キ6台,ベ−ラ4台,トレ−ラ8台のセットで演算した結果,支障なく作業できることがわかった.
また,年間の刈取状況をまとめたのが図2.8で,年間の作業状況を全体として直観的に把握できる.
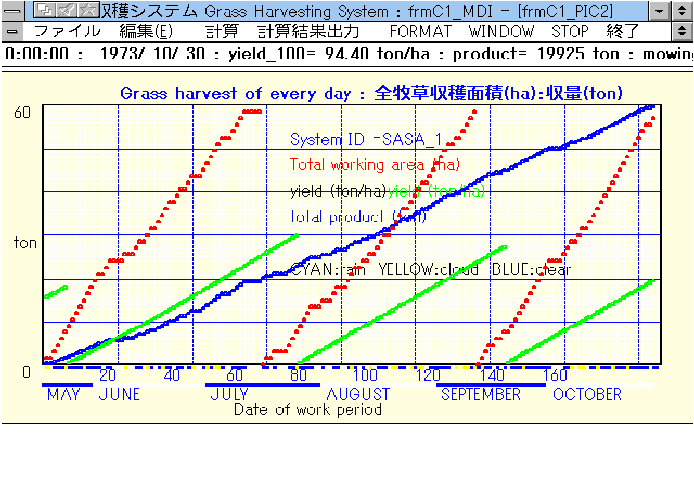
図2.8 収穫作業の進行状況(g312_4.bmp)
全般に,一・二番刈りの時期は,草処理量が順調に増加するが,三番刈りでは生育不良の期間があった.
b) 水稲作業体系の負担面積 作業体系の負担面積Hが求められると,それに対する各作業の余裕度や所要時間等の分析により,この作業体系の特徴を明らかにすることができる.
表4.3(P.157)において,負担面積率u,作業利用効率q,ha当り年間機械利用時間Tr,ha当り年間労働時間Ti,年間利用時間Tyは,次式によって求める.
u = H / Hc・100 (%) eq. 2.58
q = H / Hm・100 (%) eq. 2.59
Tr = m / (c ・ r ) ( h / ha / 年) eq. 2.60
Ti = n / (c ・ r ) ( h / ha / 年) eq. 2.61
Ty = H ・ Tr ) ( h / 年) eq. 2.62
ここで, Hc:複合負担面積(ha) r:実作業率
Hm:単純負担面積(ha) m:機械の台数
C:圃場作業量(ha/h) n:人数
負担面積率uは,ある組作業がその体系においてどのくらい能力を発揮しているかを示し,この例では18番の単一防除,15〜17番の防除の組作業においておのおの5.2,15.7%と小さく,作業能力に大きな余裕があることを示す.
同じように,作業利用効率qは,ある単一作業がその体系においてどのくらい能力を発揮しているかを示し,この例では動力散粉機や堆肥散布機の能力が大きすぎることがわかる.また,負担面積率や作業利用効率の大きい作業の能力を改善することによって,体系全体の負担面積を増加させることができる.
作業時間や機械利用時間をみると,耕起・田植・収穫等の作業が全体系の作業時間の大部分を占めていることが分かる.
また,作業人数nから,確保すべき作業員数が得られ,この体系では収穫時に最大4人が必要であり,h a当り労働時間から田植,収穫の両作業群において多くの労働時間を要することが明らかになっている.
つぎに,いくつかの作業体系を比較検討する場合には,h a当りの機械利用時間 (ΣTr ),h a当りの延労働時間 (ΣTi ),最大作業人数,負担面積等をみて,営農条件を満足するなかからh a当りの機械利用時間,延労働時間,あるいは( 4章4.4)で述べる機械利用コストの少ない体系を選択・計画する必要がある.