2.3.4 待ち行列理論 目次(第2章)へ
ライスセンタにおいては,もち込まれた生籾を張込口で受入れて乾燥等の処理ののち玄米として出荷するが,生籾の到着と籾処理(受入れ)の作業は一種のサービスシステムで,生籾の到着がシステムへの入力であり籾処理の終了がシステムの出力となる待ち行列(queue)と考えられる.
到着する生籾の量が受入れ能力より少なく,かつ生籾の到着が計画的になされれば受入れのところで待たされることなく処理されるが,一般に生籾の到着はランダムであり待ち行列をつくって受入れ口で待たされることが多く,システムの効率がわるくなる.このような問題を解析する手法として待ち行列理論(Queuing theory)がある.

図2.4 荷口の推移線
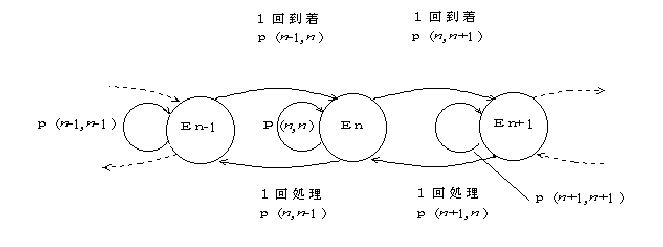
いま,ライスセンタにある生籾荷口数をn,その事象をEn,微小時間⊿tの間に1回到着する確率をλ(平均到着率,average arrival rate),1回処理が終了する確率をμ(平均サービス率,average service rate)とすると,⊿t時間に生ずる事象Enの推移確率は,つぎのようになる.
En→En+1 の推移確率 p( n, n+1 ) =λn⊿t eq. 2.32
En→En-1 の推移確率 p( n, n-1 ) =μn⊿t eq. 2.33
En→En の推移確率 p( n, n ) =( 1-λn⊿t )( 1-μn⊿t ) eq. 2.34
また,ある時刻tに事象Enである確率をPn(t) とすると,
Pn(t +⊿t) = Pn-1( t )・λn-1⊿t + Pn+1( t )・μn+1⊿t + Pn( t ) ・
( 1-λn⊿t )( 1-λn⊿t ) eq. 2.35
これから
{ Pn( t +⊿t ) - Pn( t ) } / ⊿t = λn-1・Pn-1( t ) + μn+1( t ) ・Pn+1( t ) -
( λn +μn ) ・Pn( t ) +λn・μn ・Pn( t )・⊿t eq. 2.36
ここで,⊿t → 0の極限をとると,
∴dPn( t ) / d t = λn-1・Pn-1( t ) + μn+1( t ) ・Pn+1( t ) -( λn +μn ) ・Pn( t ) eq. 2.37
システム内に生籾のない n = 0 のときは,
E0→E1 の推移確率 p(0, 1) = λ0⊿t eq. 2.38
E1→E0 の推移確率 p(1, 0) = μ1⊿t eq. 2.39
E0→E0 の推移確率 p(0, 0) = 1 - λ0⊿t eq. 2.40
したがって,
dP0( t ) / d t = μ1 ・P1( t ) - λ0 ・P0( t ) eq. 2.41
ここで,時刻tに無関係な定常過程を考え,システムが平衡状態にあるとすると,
dPi( t ) / d t = 0 ( i=1,2, ・・・) eq. 2.42
このとき,Pn(t)= pnとおくと(2.37)(2.41)式より
λn-1・pn-1 + μn+1 ・pn+1 - (λn +μn ) ・pn = 0 eq. 2.43
μ1 ・p1 - λ0 ・p0 = 0 eq. 2.44
p0 + p1 + p2 + ・・・ = 1 eq. 2.45
ここで,生籾の到着は平均λ回/hのポアソン分布にしたがうポアソン到着(Poisson arrival)とすると微小時間⊿tの間に到着する確率はλ⊿tである.また籾受入れ処理時間が平均1/μの指数分布にしたがう指数サービス(exponential service)とすると処理回数は平均μ回/hのポアソン分布となり,その間の処理終了確率はμ⊿tである.
籾受入れ口は一つで,処理数は有限でなく,システムは平衡状態と仮定すると,(2.44)式から,
p1 = (λ/μ)p0 = ρp0 eq. 2.46
ここで,ρはトラフィック密度または入荷率とよばれ,平均到着数と平均処理回数との比で,
ρ = λ/μ eq. 2.47
である.
(2.46)を(2.43)式に代入して,
p2 = ρ2p0, p3 = ρ3p0, ・・・, pn = ρnp0
が得られる.また,(2.45)式から,
p0 (1 + ρ +ρ2 + ・・・ + ρn) = 1 eq. 2.48
p0 = (1 - ρ)/ (1 - ρn+1) eq. 2.49
(2.48)式はρ<1,すなわち,平均到着数が平均処理回数より小さいとき収束し,n→∞ のとき
p0 = (1 - ρ) eq. 2.50
到着した生籾が受入れられず待たされる確率(待ち率,delay probability)をqとすると,
q = n∑i=1 pi = 1 - p0 = ρ = λ/μ eq. 2.51
到着した生籾が待たずにすぐ受入れられる確率は,
1 - q = p0 = 1 -ρ = (μ-λ)/μ eq. 2.52
行列の長さの期待値(システム内の荷口も含む)Lは,
L = ∞∑i=1 ipi = ρ/(1 - ρ) = λ / (μ-λ) eq. 2.53
実際に受入れ口の前に待たされる実質待ち行列の長さLqは,
Lq = ∞∑i=1 (i-1)pi = ρ2/(1 - ρ) = λ2 / [μ(μ-λ)] eq. 2.54
したがって処理中の生籾荷口の期待値 Ls は,
Ls = L - Lq =ρ = λ / μ = q eq. 2.55
また,生籾荷口が処理が終わるまでシステム内にいる時間を平均待ち時間Wとすると,平均待ち時間と単位時間の平均到着数λの積が待ち行列の長さLと考えられるので,
W = L / λ= 1 /(μ-λ) eq. 2.56
さらに,到着してから処理され始めるまでの平均実質待ち時間(queuing time)をWqとすると,
Wq = Lq / λ= λ /[μ(μ-λ)] eq. 2.57
●ソフトウェア 待ち行列理論:que_800.exe