b233.htmlモンテカルロ

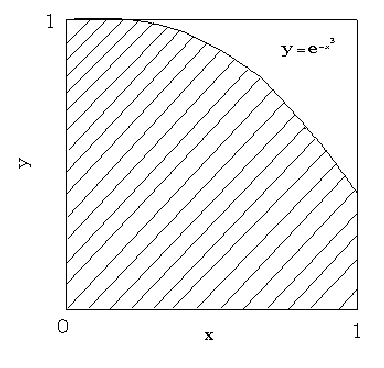
図2.3の斜線部，曲線 y = e ^{- x}^³ と直線 x = 0 , y = 0 にかこまれる部分の面積Ａを求める問題について考えてみよう．

これは定積分∫_₀^¹ e ^{- x}^³dx を求めることであるが，不定積分∫ e ^{-
x}^³dx が存在しないので不定積分を用いた解析的な手法では求めることができない．

したがって，分割法などの計算によりＡの近似値0.8075....を得ることができるが，ここでは発想を変えて乱数を用いた算出を行ってみよう．

でたらめに図2.3に向かって発射する矢のように，正方形 ( 0≦ x < 1, 0 ≦ y < 1) 内の１点（x，y）をランダムに選ぶことは，区間（0，1）の一様乱数x，yを独立に求めることによって実行できる．そこでそのようにして求めた点（x，y）について y ≦ e ^{- x}^³ ならばその点は斜線部Ａ内の点であることを用いて，正方形内の点（x，y）を数多く選んでその点の位置が斜線部の内か外かという実験を繰り返すことによって，面積Ａをつぎのように求めることができる．

　　　A = A₀ ・ N_A / N₀　　　　　　　　　　　　　　　　　　　　　eq. 2.31

表2.4は乱数表から求めたx，yを用いて行った20回の実験の結果であり，N₀ = 20，N_A = 17からA = 17/20 = 0.85を得た．

表2.4　∫_₀^¹ e ^{- x}^³dx の値を求めるモンテカルロ実験

一様乱数			y ≦ e ^{- x}^³	一様乱数			y ≦ e ^{- x}^³
x	y	e ^{- x}^³		x	y	e ^{- x}^³
59	18	0.814	*	76	67	0.645
04	07	0.999	*	75	51	0.656	*
98	37	0.390	*	77	40	0.633	*
84	51	0.553	*	55	59	0.847	*
90	00	0.482	*	51	33	0.876	*
78	51	0.622	*	35	69	0.958	*
99	80	0.379		27	28	0.981	*
79	58	0.611	*	72	34	0.688	*
70	73	0.710		21	95	0.991	*
82	13	0.576	*	31	25	0.971	*

　この実験の回数を何千何万と増すことによってさらによい近似値を得ることができよう．

　このように元来決定論的な問題を確率論的な手法を用いて説くことができるのは興味深いことである．このように乱数を用いて算出する手法をモンテカルロ法（Monte Carlo method）とよんでいる．

また，モンテカルロ法を用いた確率的モデルを用いて多数回の実験を行い，統計的システム解析を行うことをモンテカルロシミュレーションとよぶ．