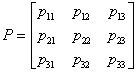b232.htmlマルコフ連鎖

2.3.2　マルコフ連鎖　　　　　　目次（第２章）へ

起こりうる事象は E₁, E₂,・・・, E_nの n通りあって，第１番目，第２番目，…と順次の試みによって，どれかの事象がおこるものとする．第m番目の試みの結果は，それ以前の第 (m-1) 番目の試みの結果に関係して定まるとき，この一連の試みをマルコフ連鎖（Markov chain）という．とくに第m番目の試みの結果が，その直前，すなわち第 (m-1) 番目の試みの結果にだけ関係するとき，これを単純マルコフ連鎖という．

　　＊マルコフ連鎖計算プログラム

2.3.2.1 推移確率　

　単純マルコフ連鎖でE_jのつぎにE_kのおこる条件つき確率を，E_jからE_kへの推移確率といいp_jkで表す．また，

	│	p₁₁	p₁₂	・・・	p_1n	│
P =	│	p₂₁	p₂₂	・・・	p_2n	│	eq. 2.10
	│	・・・				│
	│	p_n1	p_n2	・・・	p_nn	│

を推移確率マトリックスという．各行の要素の和は1に等しい．すなわち

∑ p_jk = 1 　　　　　　　　　　　　　　　　　　eq. 2.11
　k

である．第１番目の試みの前の状態，すなわち初期の状態が E₁, E₂,・・・, E_nである確率をそれぞれ

q₁, q₂,・・・, q_n

で表し，これらを初期確率とよぶ．

2.3.2.2 高次の推移確率

　毎日の天候は晴天（雨でない日）A₁または雨天A₂のいずれかであり，単純マルコフ連鎖とする．1年の天候についてみると,元旦は晴天か雨天かは前日（前年の末日）の天候によって確率的に定まり,2日以降も順次前日の天候によって確率的に定まるものとする．

　いま前日が晴天A₁である場合，つぎの日に晴天A₁を継続する確率をp₁₁,雨天A₂に変更する確率をp₁₂,前日雨天A₂である場合，つぎの日に晴天A₁に変更する確率をp₂₁,雨天A₂を継続する確率をp₂₂とする．

　このマルコフ連鎖の推移確率マトリックスは

	│	p₁₁	p₁₂	│
P =	│	p₂₁	p₂₂	│	eq. 2.12

となり，その推移線図は図2.2のようである．

図2.2　天候の推移線図（BPSE2-2.JBH）

　図2.2のように，推移の状態を図示したものを推移線図またはシャノン(Shannon)線図という．これに推移確率を記入することによってマルコフ連鎖が示される．

　前年末日の天候が晴天A₁である場合，第２日目にA₁またはA₂になる確率をそれぞれp₁₁⁽²⁾,p₁₂⁽²⁾で表せば

p₁₁⁽²⁾ = Pr｛第１日 A₁,第２日 A₁｝ + Pr｛第１日 A₂,第２日 A₁｝

　　　　　= p₁₁p_{11
+}p₁₂p₂₁　　　　　　　　　　　　　　　　eq. 2.13

p₁₂⁽²⁾ = Pr｛第１日 A₁,第２日 A₂｝ + Pr｛第１日 A₂,第２日 A₂｝

　　　　　= p₁₁p_{12
+}p₁₂p₂₂　　　　　　　　　　　　　　　　eq. 2.14

である．同様にして，前年末日の天候が雨天A₂である場合，第２日にA₁,A₂になる確率はそれぞれ

p₂₁⁽²⁾ = p₂₁p_{11
+}p₂₂p₂₁　　　　　　　　　　　　　　　　eq. 2.15

p₂₂⁽²⁾ = p₂₁p_{12
+}p₂₂p₂₂　　　　　　　　　　　　　　　　eq. 2.16

となる．これらを２次の推移確率という．２次の推移確率マトリックスは

eq. 2.17

となり，推移確率マトリックス(p_jk^(m))はp^(m)で表される．

　　　　　　　　　　　　eq. 2.18

　eq. 2.19

P^m = P ・ P^m-1 = P^k ・ P^m-k 　　　　　　　　eq. 2.20

前年末日が晴天である確率をq₁,雨天である確率をq₂とすると，初期天候ベクトルq は，

q = (q₁,q₂)　　　　　　　　　　　　　　　　　　　 eq. 2.21

元日に晴天A₁になる期待値q₁⁽¹⁾は，

q₁⁽¹⁾= q₁p₁₁ + q₂p₂₁　　　　　　　　　　　　　 eq. 2.22

元日に雨天A₂になるq₂⁽¹⁾は，

q₂⁽¹⁾= q₁p₁₂ + q₂p₂₂　　　　　　　　　　　　　 eq. 2.23

したがって，元日の天候ベクトルq⁽¹⁾は，

q⁽¹⁾= (q₁⁽¹⁾ , q₂⁽¹⁾)　　　　　　　　　　　　　

　　= qP　　　　　　　　　　　　　　　　　　　　 eq. 2.24

第２日目以降についても同様にして

q⁽²⁾= qP^²　　　　　　　　　　　　　　　　　　　　 eq. 2.25

q^(m)= qP^{^m}　　　　　　　　　　　　　　　　　　　　 eq. 2.26

2.3.2.3 定常マルコフ連鎖

　推移確率マトリックスPの要素P_jkがすべて正の場合，m次の推移確率マトリックスPはmの増加にしたがって，各行が同じ確率ベクトル t = (t₁, t₂,・・・, t_n) の成分からなるマトリックス

eq. 2.27

に近づき，確率ベクトルtの成分t_iはすべて正であるといわれている．

　このことは，q を任意の初期確率ベクトルとすれば，

q^(m)= qP^{^m}　　　　　　　　　　　　　　　　　　　　 eq. 2.28

は m の増加とともに t = (t₁, t₂,・・・, t_n) に近づくことを示している．したがって初期確率ベクトルとしてtを選べば

tP = t,　　　　　　　　　　　　　　　　　　　　　　 eq. 2.29

t = tP =tP² = ・・・ = tP^{^m} 　　　　　　　　　eq. 2.30

である．(2.29)式で定まる t を推移P の不動確率ベクトルという．不動確率ベクトルを初期確率にとれば，(2.30)式からわかるように，ある状態にある確率は，この連鎖を通じて一定である．とくにこのようなマルコフ連鎖を定常マルコフ連鎖という．

●ソフトウェア

2.3.2.4 天候のマルコフ連鎖

　ある日の天候は，晴晴率5/6，雨晴率2/3の単純マルコフ連鎖現象と仮定できる．推移確率マトリックスPを示せ．また，長期間の日数では，晴天率Cと雨天率Rは，不動確率ベクトルtで示される．CとRを求めよ（ここで，晴晴率，雨晴率とは，前日が晴または雨であったとき，本日が晴になる確率のことである）．

　解．　

　また，t・P = tかつ，C + R = 1

∴ p₁₁・C + p₂₁・R = C 　　(a)

p₁₂・C + p₂₂・R = R 　　　　(b)

C + R = 1　　　　　　　　　 (c)

　(a)より p₂₁・R = (1 - p₁₁) ・ C

R = ( p₁₂ / p₂₁) ・ C

　これを(c)に代入し

C + ( p₁₂ / p₂₁) ・ C = 1

( p₂₁ + p₁₂ ) / p₂₁・ C = 1

∴ C = p₂₁/ ( p₂₁ + p₁₂ )

∴ R = p₁₂/ ( p₂₁ + p₁₂ )

これから R = 0.2, C = 1.8 が得られる．

また，天候を晴天，曇天，雨天の三つに分類したときの推移確率マトリックスは表2.3のようになる．

表　2.3　天候（晴天, 曇天, 雨天）の期待値の推移

	A1：晴	A2：曇	A3：雨	マトリックス
初　日	q₁	q₂	q₃	q = ｛q_1,q_2,q₃｝
２日目	q₁⁽¹⁾₌q₁ ・p₁₁ ₊q₂ ・p_{21 +}q₃ ・p₃₁	q₂⁽¹⁾₌q₁ ・p₁₂ ₊q₂ ・p_{22 +}q₃ ・p₃₂	q₃⁽¹⁾₌q₁ ・p₁₃ ₊q₂ ・p_{23 +}q₃ ・p₃₃	q⁽¹⁾ = q ・P
３日目	q₁⁽²⁾₌q₁⁽¹⁾ ・p₁₁ ₊q₂⁽¹⁾ ・p_{21 +}q₃⁽¹⁾ ・p₃₁	q₂⁽²⁾₌q₁⁽¹⁾ ・p₁₂ ₊q₂⁽¹⁾ ・p_{22 +}q₃⁽¹⁾ ・p₃₂	q₃⁽²⁾₌q₁⁽¹⁾ ・p₁₃ ₊q₂⁽¹⁾ ・p_{23 +}q₃⁽¹⁾ ・p₃₃	q⁽²⁾ = q⁽¹⁾ ・P 　　= q ・P²
４日目	q₁⁽³⁾₌q₁⁽²⁾ ・p₁₁ ₊q₂ ⁽²⁾・p_{21 +}q₃⁽²⁾ ・p₃₁	q₂⁽³⁾₌q₁⁽²⁾ ・p₁₂ ₊q₂⁽²⁾ ・p_{22 +}q₃⁽²⁾ ・p₃₂	q₃⁽³⁾₌q₁⁽²⁾ ・p₁₃ ₊q₂⁽²⁾ ・p_{23 +}q₃⁽²⁾ ・p₃₃	q⁽³⁾ = q ・P³
***	・・・	・・・	・・・	・・・

ここで，

次章 2.3.3 モンテカルロシミュレ－ション　へ