 |
| 図.1 分布数えソート |
|---|
今回のソート法は非常に限定的です。しかし、頭の片隅に置いておくと意外なところで役に立つかもしれませんよ。
では、今回の要点です。
では、いってみましょう。
今回のソート法は今までのソート法とは少し違います。今までのソート法はデータを交換していきました。が、今回のソート法にはデータの交換は全くありません。
では、どんなソート法なのでしょうか?
先ず、どのデータが何個あるかを調べます。そして、データを小さいものからその個数だけ配列に書き込んでいきます。すると、もうソートができています。これを分布数えソートと呼びます。
と、説明速すぎますね。では、図でも見てみましょう。
 |
| 図.1 分布数えソート |
|---|
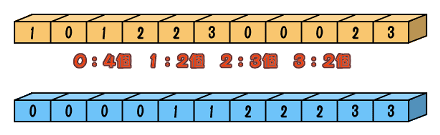
先ず、データが0〜3の値しかとらないとします。そして、0〜3のデータがそれぞれ何個あるかを数えていきます。上の配列では、0は4個、1は2個、2は3個、3は2個です。
そして、元の配列に0を4個、1を2個、2を3個、3を2個書き出せば、ソートが完了します。
何か騙されたようですが、間違いなくソートできます。そして、いろいろ面倒なことをしないので、数あるソート法の中でも最も速いソート法となります。データが0〜255しかない100万要素の乱数列を、わずか0.2秒でソートしてしまいます(MMXペンティアム300MHz)。同じデータをクイックソートでソートしたところ、1.6秒かかりました。
これを構造体の1メンバを使ったソートに応用することもできます。しかし、ソートする配列と同じ大きさのバッファを必要とします。
例えば上の例を使うと、0は1〜4番目に、1は5〜6番目に、2は7〜9番目に、3は10〜11番目に来ますね。各組の最後が何番目かは、上で数えた個数を順に足していけば分かります。0の個数を1の個数を足すと6で、1の組の最後の位置になります。そして、この6を2の個数と足すと9になり、2の組の最後に位置になります。これを数えるのに使ったバッファ上で計算します。
要素をどの位置にもっていったらソートできるかが分かったので、あとはこの情報を元にソートすることができます。しかし、元の配列を上書きしながらソートすることはできません。一旦バッファへソートして、それから一括して元の配列に上書きすることになります。
では、例を見てみましょう。
| プログラム |
|---|
// Sort8.cpp
#include <stdio.h>
#include <stdlib.h>
#include <memory.h>
struct SData // データ
{
int nKey1;
int nKey2;
};
const int DATA_SIZE = 64; // データの個数
const int DATA_MAX = 200; // データの最大値
const int DATA_MIN = 100; // データの最小値
const int DATA_KINDS = (DATA_MAX - DATA_MIN + 1); // データの種類数
SData g_adata[DATA_SIZE]; // 元データ
SData* g_apdata[DATA_SIZE]; // データへのポインタ
// データを設定する
void SetData()
{
int i;
for(i = 0; i < DATA_SIZE; i++)
{
g_adata[i].nKey1 = rand() % DATA_KINDS + DATA_MIN;
g_adata[i].nKey2 = rand() % DATA_KINDS + DATA_MIN;
g_apdata[i] = &g_adata[i];
}
}
// データを表示する
void DispData()
{
int i;
for(i = 0; i < DATA_SIZE; i++)
printf("(%d, %d)", g_apdata[i]->nKey1, g_apdata[i]->nKey2);
putchar('\n');
}
// 分布数えソート
// bKey1 が true の時は nKey1 を使ってソート
// bKey1 が false の時は nKey2 を使ってソート
void DCSort(bool bKey1)
{
SData* apdataTemp[DATA_SIZE]; // ソートのためのバッファ
int anCount[DATA_KINDS]; // 勘定のためのバッファ
int nKey; // キー
int i;
// 分布を数える
memset(anCount, 0, sizeof anCount);
for(i = 0; i < DATA_SIZE; i++)
{
nKey = bKey1 ? g_apdata[i]->nKey1 : g_apdata[i]->nKey2;
anCount[nKey - DATA_MIN]++;
}
// 各組の最後の要素の位置を計算
for(i = 1; i < DATA_KINDS; i++)
anCount[i] += anCount[i - 1];
// ソート
for(i = DATA_SIZE - 1; i >= 0; i--)
{
nKey = bKey1 ? g_apdata[i]->nKey1 : g_apdata[i]->nKey2;
apdataTemp[anCount[nKey - DATA_MIN] - 1] = g_apdata[i];
anCount[nKey - DATA_MIN]--;
}
// 結果をコピー
memcpy(g_apdata, apdataTemp, DATA_SIZE * sizeof *g_apdata);
}
int main()
{
SetData();
DCSort(false); // 先に nKey2 でソートして
DispData();
DCSort(true); // 次に nKey1 でソートする
DispData();
return 0;
}
|
| 実行結果 |
(174, 100)(117, 103)(195, 105)(186, 107)(186, 108)(194, 111)(183, 111)(152, 113) (151, 115)(199, 118)(177, 118)(112, 119)(121, 120)(196, 122)(134, 122)(171, 123) (166, 124)(125, 124)(171, 124)(174, 124)(183, 125)(149, 131)(139, 132)(180, 132) (112, 133)(139, 133)(192, 135)(172, 138)(113, 139)(137, 145)(194, 148)(147, 149) (164, 152)(171, 152)(151, 154)(146, 157)(149, 159)(171, 160)(190, 160)(151, 161) (172, 161)(159, 162)(133, 163)(194, 165)(160, 165)(149, 167)(165, 168)(180, 169) (175, 170)(195, 171)(157, 171)(108, 172)(119, 176)(102, 178)(180, 183)(139, 184) (158, 184)(141, 185)(163, 187)(158, 194)(167, 197)(123, 199)(129, 199)(135, 199) (102, 178)(108, 172)(112, 119)(112, 133)(113, 139)(117, 103)(119, 176)(121, 120) (123, 199)(125, 124)(129, 199)(133, 163)(134, 122)(135, 199)(137, 145)(139, 132) (139, 133)(139, 184)(141, 185)(146, 157)(147, 149)(149, 131)(149, 159)(149, 167) (151, 115)(151, 154)(151, 161)(152, 113)(157, 171)(158, 184)(158, 194)(159, 162) (160, 165)(163, 187)(164, 152)(165, 168)(166, 124)(167, 197)(171, 123)(171, 124) (171, 152)(171, 160)(172, 138)(172, 161)(174, 100)(174, 124)(175, 170)(177, 118) (180, 132)(180, 169)(180, 183)(183, 111)(183, 125)(186, 107)(186, 108)(190, 160) (192, 135)(194, 111)(194, 148)(194, 165)(195, 105)(195, 171)(196, 122)(199, 118) |
分布数えソートのいいところは、同じ値の要素の位置関係が保たれる所です。このような性質を安定であると呼びます。これは高速なソート法であるクイックソート、シェルソートにはない特色です(ただし、バブルソートなど、低速なソート法は大抵安定です)。
例えば、上の赤、橙、青で色付けられたところを見て下さい。先に nKey2 でソートしているので、nKey1 でソートした後でも nKey2 の大小関係が保存されています。他の所もそうなっているはずです。高速で、なおかつ安定なソート法。それが分布数えソートなのです。
それでは、何故このソート法が広く使われないのでしょうか? それは、このソート法の適用範囲が限定されているからです。
先ず、データの種類数が決まっていなければいけません。数を数えるのに使うバッファのサイズが決まっていなければならない、という制約があるからです。バッファのサイズはデータの種類数だけ必要ですね。動的に確保することもできますが、それでは遅くなってしまいます。
上の配列では「データが0〜3しかない」と限定されています。すると、各データの個数を数えるために
int nCount[4];
という変数を作ることになります。データが0〜999なら
int nCount[1000];
となります。
そして、ここで分かるようにデータの種類が多すぎると問題があります。
例えば、int のとりうる値全てをとるとすると、種類が多すぎてバッファを作ることができません。それでなくても、あまりに種類が多いとデータを展開するときに時間がかかりすぎます。小さい配列であれば、単調にデータをソートした方が速くなってしまうでしょう。
ということで、分布数えソートは限定的にしか使えません。しかし、もし使えるところがあれば、その性能をいかんなく発揮してくれることでしょう。使う機会は少ないかも知れませんが、頭の片隅にでも置いておいてはどうでしょうか?
それでは、今回の要点です。
これでソートは終わりです。ヒープソート、マージソートなど、他にもソート法はありますが、これ以上話すのもくどいので軽く話して終わりにします。
ヒープソートは速度が安定しているという特徴があります。同じサイズの配列のソートにかかる時間は一定という性質があります。速度の大きさよりもその安定性を重視したいときは、クイックソートよりはヒープソートの方が適していると言えます。
ただ、アルゴリズムは若干難解です。Fussy さんのHPで詳しく解説されているので、そちらを参考にしてみてはいかがでしょうか?
マージソートはデータを2つずつの組に分割し、それをそれぞれソートし、それを合成していくことでソートを行います。合成するときは、2つのデータの先頭を見て小さいものから書き出していきます。
確かに高速なのですが、マージソートはデータと同じサイズのバッファを必要とするのが欠点です。データサイズが限られているような配列のソートに使うといいでしょう。
次回は数値検索をやってみたいと思います。それでは。
Last update was done on 2000.10.23
この講座の著作権はロベールが保有しています