

| ○ |
非直線インダクター インダクタンスが非直線的といっても少なくとも2種類の性質が考えられますが、これら は別のやりかたでモデル化します。 (1) 周波数依存性インダクター 別原稿 周波数依存インダクター (2) 電流依存性・ヒステリシスのあるインダクター |
||||||||||||||||||||||||||||||||||||
| ● |
(1) 周波数依存性インダクター この種の非直線性は、周波数依存抵抗と周波数依存インダクタンスの組み合わせで 表されます。 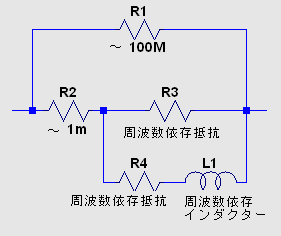 まずはインダクタンスと直列抵抗 Rser をシミュレーション測定する手段の 確認から始めます。 このページを作るに当たって http://www.coilcraft.com/modelspspice.cfm は 大変参考になりました。 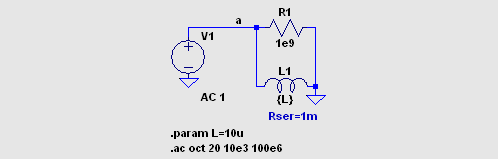 グラフは上から順に、電源電流、インダクタンス、直列抵抗、インピーダンスと位相角 (360 分度)、位相角のみ、Q の値です。 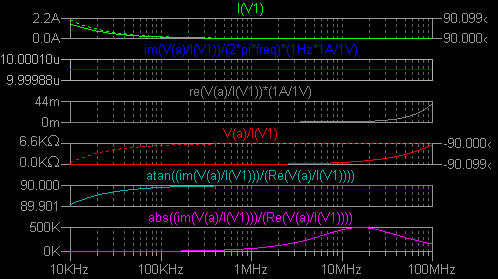 測定周波数を 10MHz として、この測定法の適用範囲を調べました。
赤字の部分は全く信頼できない値です。 しかしインダクタンスの値は正確に求まります。 |
| ・ |
周波数依存性のある抵抗は次のように表現され
ます。 G1 は周波数に無関係な、G2 は周波数に比例する、G3 は周波数の平方根に比例する
抵抗値を示します。 グラフの縦軸は抵抗値です。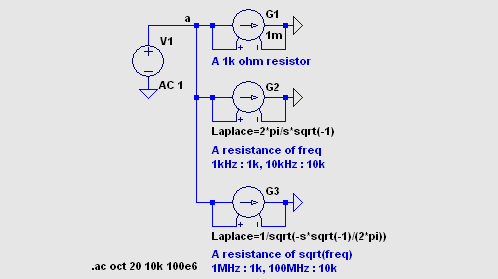 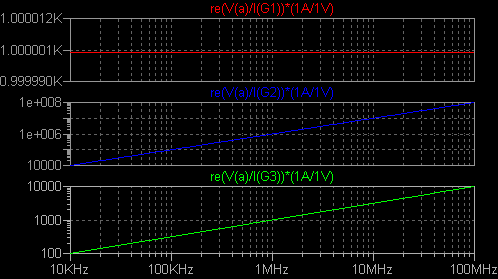 普通、周波数依存インダクターには周波数の平方根に比例する抵抗を使用します。 これの物理的意味は あるのでしょうが、私の理解の範囲を超えます。 とりあえず、周波数の平方根に比例する抵抗を使うと 現実のインダクターがうまくシミュレートできるとして先に進みます。 Coilcraft 社の説明文では、周波数の平方根に比例する抵抗を 1/(k*sqrt(s/(2*pi))) と 書いて、周波数と抵抗値の具体的な対応関係は k で設定します。 以下この表記法を使います。 |
| ・ |
インダクタンスを Laplace 式で表現することができます。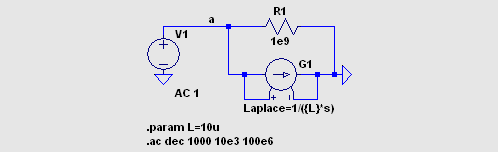 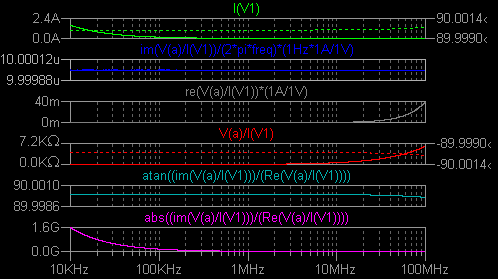 nl_ind2.asc nl_ind2.plt (並列コンデンサーを接続して共振させてみると、インピーダンス V(a)/I(V1) の グラフの位相角は正常なのですが、位相角のみの グラフ atan((im(V(a)/I(V1)))/(Re(V(a)/I(V1)))) の表示値が不審です。 御注意下さい。) 周波数依存性のあるインダクタンスは次のように表します。 これも Coilcraft 社の説明文の書式に合わせました。 1/(s*(k3-(k4*ln(k5*(s/(2*pi)))))) 1/(1e-6*s*(k3-(k4*ln(k5*(s/(2*pi)))))) (μH 単位で表す場合) |
| ・ |
実際のカタログには、さらにモデルの周波数適用範囲ごとにパラメーターが記されてい
ます。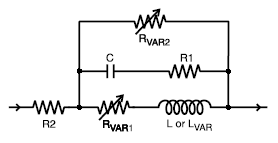
これを LTspice の書式に書き直してシミュレーション測定しました。 グラフは上から インダクタンス、直列抵抗、インピーダンスと位相角、Q の値です。 まずは 0.1 〜 0.6MHz の モデルを調べます。 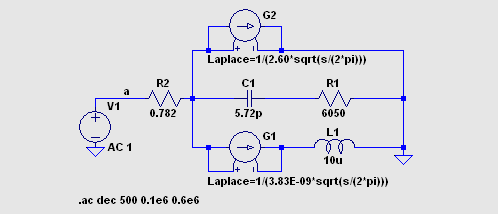 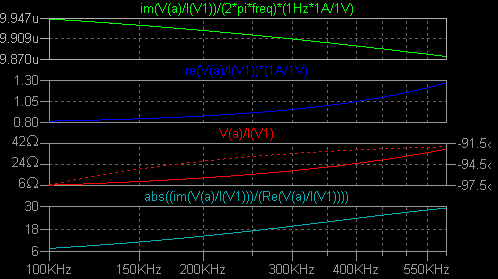 3つをまとめました。 3つの .ac ディレクティブのうちの一つだけを生かして実行します。 対応 する nl_ind3?.plt を Plot Settings → Open Plot Settings File で選択して使います。 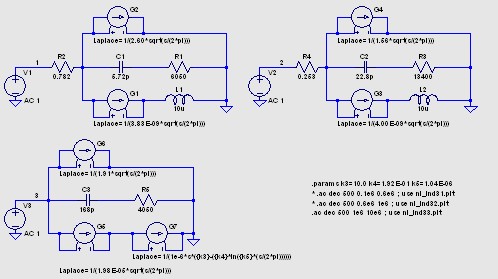 0.6 〜 1MHz 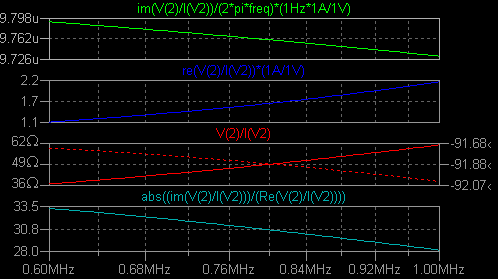 1 〜 10MHz 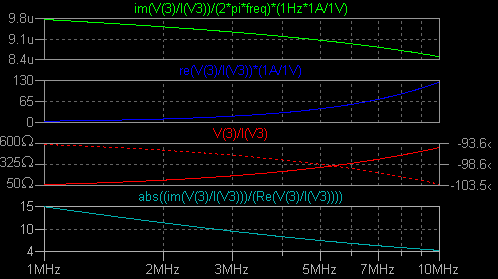 nl_ind3.asc nl_ind31.plt nl_ind32.plt nl_ind33.plt 3つの周波数帯のグラフの連続性は、なぜかあまりよくありません。 もう少し追求してみる つもりです。 なおこのモデルで過渡解析を行うときは直列抵抗が必須です。 |
||||||||||||||||||||||||||||||||||||||||||||||||
| ● |
(2)
電流依存性・ヒステリシスのあるインダクター たとえばコンデンサーには寄生素子のほかに電圧依存性を指定することが できます。 抵抗は温度係数を指定することができます。 しかしながら インダクターに関してはもっと複雑な指定ができます。 基本的なインダクターには 3つの寄生素子、つまり直列抵抗 Rser、端子間の並列抵抗 Rpar および並列容量 Cpar が 考慮されています。 インダクタンスの温度係数 (一次および二次) も指定可能です。 インダクタンスの電流依存性やヒステリシスに関して、LTspice では数式で磁束 (flux) を 指定する動作モデルと、ヒステリシス特性のあるコアの動作に基づいた モデルの二種類が利用できます。 このほかにもいろいろと工夫するやりかたもあって、Web 検索 すると議論が続いていることがわかります。 ちょっと困ったことに、このあたりの話になると SPICE の「方言」の違いや、SPICE の 版によっても表記方法が異なったりすることに注意しなくてはなりません。 |
| ・ |
(2-1)
数式で磁束 (flux) を指定する動作モデル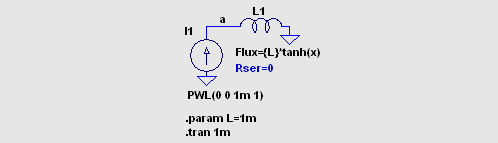 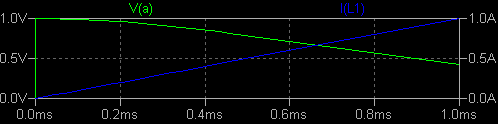 nl_ind4.asc nl_ind4.plt L1 には時間微分が一定の電流を流していますので、その両端電圧はインダクタンスに 比例します。 I(L1) が大きくなると両端電圧 V(a) が小さくなっていますが、これは インダクタンスが電流によって飽和していることを表します。 この例では 約 330mA でインダクタンスが 0.9 倍に減少しています。 Flux= 式の {L} がインダクタンスを、tanh(x) が飽和特性を決めています。 x は特別な キーワードで、インダクタンスに流れる電流を意味します。 tanh() に 特別な数学上の意味はなく、単に飽和する関数としての用途です。 x に 1 より大きい 係数を乗じれば、より少ない電流で飽和します。 とてもハードな飽和特性が欲しいのなら、tanh() の代わりに limit() を使い ます。 もっとソフトな飽和特性が望みなら atan() を使います。 tanh() と atan()/57.3 の グラフの形は次のようなものです。(0 付近の傾きを合致させました。) 実際 に atan() を Flux= 式に記述するときは /57.3 を除外して下さい。 パラメーターと しての V(x) は PWL を使って -3 から +3 まで変化させています。 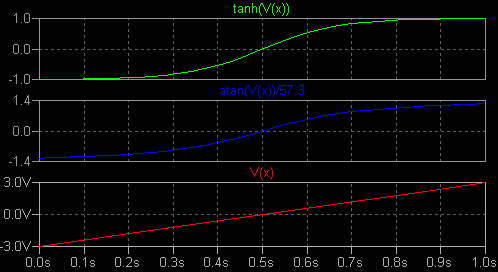 ・よりスマートな記述のしかたを Web 上で見つけました。 Flux = {L}*x ; 飽和なし Flux = {L}*limit(x,{-Is},{Is}) ; ハードな飽和。Is は飽和電流。 Flux = {L-Ls}*limit(x,{-Is},{Is})+{Ls}*x ; ステップ型の飽和、Ls は飽和後のインダクタンス。 Flux = {(L-Ls)*Is}*tanh(x/{Is})+{Ls}*x ; ソフトな飽和 Flux = {L*Is*2/pi}*atan(x/{Is*2/pi}) ; さらにソフトな飽和 |
| ・ | (2-2)
ヒステリシス特性のあるコアの動作に基づいたモデル これは Help → LTspice → Circuit Elements → L. Inductor の後半部分で けっこう詳しく説明されています。 磁気コアの性質を3つのパラメーターのみで指定します。 保磁力 Hc (A/m) 残留磁束密度 Br (T) 飽和磁束密度 Bs (T) これに加えて、コアのサイズ等を指定します。 磁気回路長 Lm (m) ギャップ長 Lg (m) コア断面積 A (m^2) 巻き数 N (回) まずは測定方法の確認です。 50mH の理想インダクターに時間微分が一定の 電流を流し、両端電圧とその時間積分を表示しました。 時間積分には「おぼえ書き (使い方メモ)」で 紹介した idt() を使っています。 問題がなさそうな場合は便利に使わせてもらいましょう。 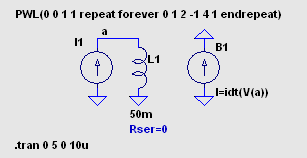 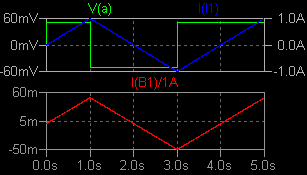 I(B1)/1A すなわち idt(V(a)) は磁束密度の目安になります。 縦軸の値は任意です。 次に Inductor の Help に例として示されている、パラメーターが Hc=16. Bs=.44 Br=.10 ・・ の コイルに置き換えます。 Rser はデフォルトの 1mΩです。 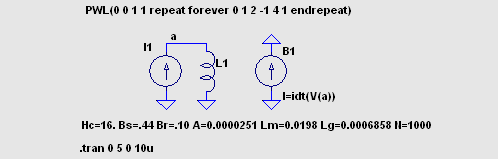 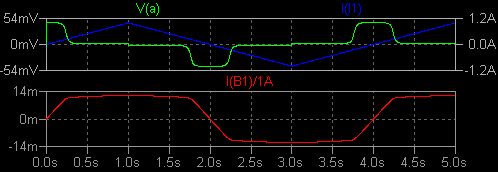 微小電流領域でのインダクタンスは 46mH 程度です。 200mA ほどの電流で インダクタンスが 0.9 倍に減少します。 このインダクターのエアギャップ は 0.7mm とかなり大きいですから、ヒステリシス特性はうまく読み取れません。 そこで Lg=0 とし、このままではすぐに飽和してしまうので流す電流の最大値を ±5mA に 変更しました。 (PWL(0 0 1 5m repeat forever 0 5m 2 -5m 4 5m endrepeat)) 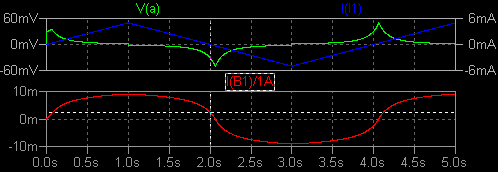 電流 I(I1) が 0 のとき、磁束密度の目安 I(B1)/1A は 0 でないことがわかり ます。 これが残留磁束密度 Br を表しています。 I(B1)/1A のグラフの 1.0s 〜 3.0s の部分を切り取って時間反転させ、これを 3.0s 〜 5.0s の上に重ね書きする と、B-H ヒステリシス特性のメジャーループのグラフになります。 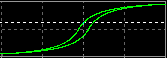 以上は正負対称の電流を流しましたが、一方向だけで増減する電流を流して みました。 (PWL(repeat forever 0 0 1 5m 2 0 endrepeat)) 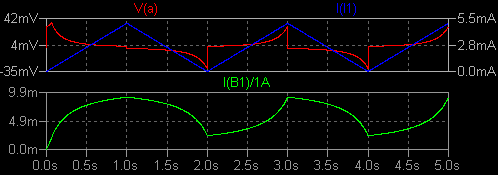 I(B1)/1A のグラフの 2.0s 〜 3.0s、3.0s 〜 4.0s の範囲を切り取って、後者の時間軸を 逆向きにして重ねると、B-H カーブのマイナーループの形になります。 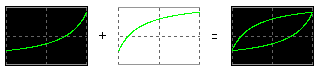 なお、この John Chan 氏によって提案されたモデルについては、今でも批判・異論があるようです。 nl_ind5.asc nl_ind5.plt |
| ● | 前項 (2-2) に記した B-H カーブなどについて、
自動的に描画する方法がわかりましたので追記します。 飽和し、かつヒステリシスがある
インダクターを例にとって説明します。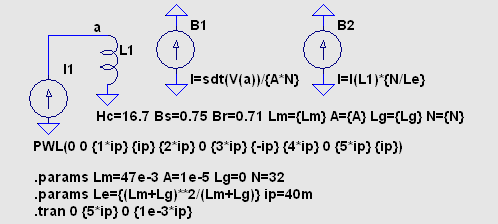 パラメーターの ip は L1 に流す電流のピーク値であると共に、I1 の PWL() の時間パラメーターに なっています。 この設定だと ip を変えても I1 電流の時間変化率は 1A/s で一定になり ます。 結果を次のようにグラフ化しました。 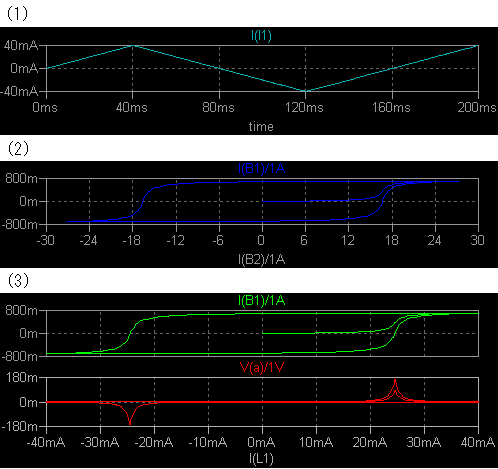 第一のグラフは時間対 I(L1) です。 第二のグラフの横軸は磁場 H で単位は A/m、縦軸は 磁束密度 B で単位は T (テスラ) です。 コアの保磁力 Hc は 16.7 で、確かにその程度の 値になっています。 飽和磁束密度 Bs = 0.75 も確かに読み取れます。 第三のグラフの横軸は I(L1) で、縦軸は磁束密度 B および L1 の端子間電圧 V(a) で す。 ヒステリシスのないインダクターなら、V(a) でインダクタンスを直読できるところです。 初透磁率の部分だけを見たい場合は .tran のパラメーター {5*ip} を {ip} に変え ます。 なお Le はギャップ長を考慮した等価磁路長です。 sat-hys-ind.asc sat-hys-ind.plt |
| もどる |
| |