時空を曲げるブラックホール

Last Update： 11/14/2012

　前のページではブラックホールを「マル」として表しました。しかしこれはあまり適切ではありません。ブラックホールの強い重力により、時空自体が大きく曲がります。ブラックホールとはこの時空の曲がり自体のことです。

　この点については詳しく説明しませんが、ブラックホールが時空を曲げる様子だけを見てみましょう。

　まず物体がない時、時空は単純で「たいら」です。

平面上が空間です。（我々が住むのは３次元空間ですが、視覚化する都合上２次元の平面で表しています）。

　物体があると、時空は曲がります。しかしふつう時空の曲がりはごくわずかです。たとえば太陽が時空を曲げる様子をまじめに描いても「平ら」と見分けがつきません。そこで太陽が時空を曲げる様子を200倍に拡大してみましょう：

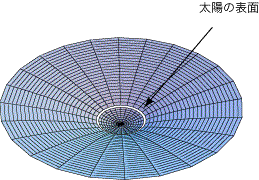
（すきまの部分が太陽の表面をあらわしています）200倍に拡大しても、時空の曲がりの効果はごくわずかであることがわかります。

　太陽と比べると、ブラックホールは重力が強く、時空を大きく曲げてしまいます（ここでは曲がりの効果を誇張していません）：

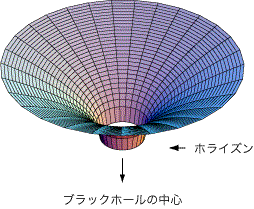
図の中心方向が、ブラックホールの中心です。また、ラッパのような形が下でとぎれています。この場所はホライズンと呼ばれます（あるいは事象の地平線や地平面などとも呼ばれる）。前のページで「ブラックホールの直径は約6 km」と書きましたが、これはホライズンの直径のことです。ホライズンの外から出た光は、私たちに届きます。しかし、ホライズンやホライズンの内側から出た光は、けっして私たちに届くことはありません。

　図はホライズンでとぎれていますが、時空は実際にはブラックホールの中心まで続いています。とぎれているのは、絵を描けないからです。ホライズンの内側では時空があまりに大きく曲げられるので、もはやこのような図では描けないのです。

　これから先は簡単化のため、またブラックホールを「マル」として描くことにします。

より詳しいコメント：
　 これはシュワルツシルト解の「埋め込みダイヤグラム」です。面は、ブラックホールの赤道面上で切った空間を表しています。（ブラックホール時空の周りで、適当に取った２つの点の距離は、この曲面上で対応する２点間の距離に等しくなっています。）このようなダイヤグラムでは、ブラックホールが空間をどう曲げているかを表すことはできますが、時間をどう曲げているかを表すことはできません。
　太陽の場合は、内部が一定密度という単純な場合で描いてあります。一定密度というのは、あまり現実的ではありません。
　ホライズンの内側に対して図を描けない一つの理由は、ホライズンの内側では空間がむしろ時間の役割を果たすからです。