（２９）三角形の四心

三角形には、４つの中心があります。「内心」、「外心」、「重心」、「垂心」の4つです。

まずは、「内心」。
内心は、三角形の３つの内角の二等分線の交点。３辺から等しい距離にある点。
三角形の3つの内角の二等分線が一点で交わることは知っていますね？
試しに、下の三角形ＡＢＣで作図してみてみると、

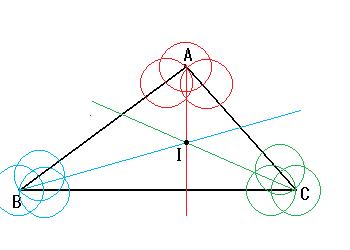
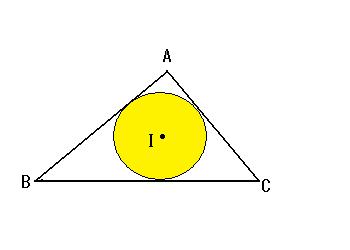
一点 Ｉ で３つの二等分線は交わります。この点を中心として、3つの辺に接する円が書くことができます。これを内接円といい、その中心 Ｉ を内心といいます。


次は「外心」。
外心は、三角形の３つの辺の垂直二等分線の交点。３つの頂点から等しい距離にある点。三角形の3つの辺の垂直二等分線が一点で交わることは知っていますね？
試しに、下の三角形ＡＢＣで作図してみてみると、

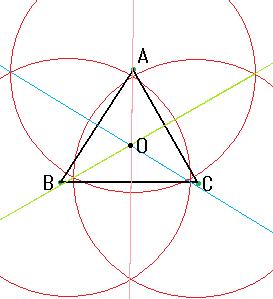
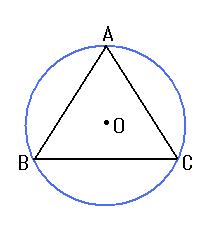
一点Ｏで３つの二等分線は交わります。この点を中心として、3つの頂点に接する円を書くことができます。これを外接円といい、その中心Ｏを外心といいます。


次は、「重心」。
重心は、三角形の3つの中線（頂点とそれに向かい合う辺の中点とを結ぶ線分）の交点。
三角形の3つの中線が一点で交わることは知っていますね？
試しに、下の三角形ＡＢＣで作図してみてみると、

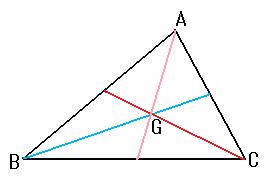
一点Ｇで３つの中線は交わります。その交点Ｏを重心といいます。
重心は、中線を１：２に分けます（中学生で証明できます）。
この重心は、均質な素材で三角形を作った場合、実際の重さの中心にもなります。

最後は、「垂心」。
垂心は、三角形の3つの垂線の交点。
三角形の3つの垂線も一点で交わります。
下の三角形ＡＢＣで３つの垂線を書くと（作図は省略します）、

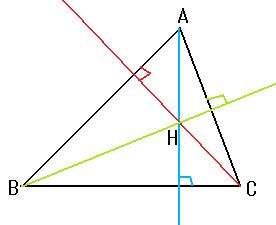
一点Ｈで３つの垂線は交わります。その交点Ｈを垂心といいます。

ちなみに、1つの三角形の外心Ｏ、重心Ｇ、垂心Ｈは、同一直線上にあり、
ＯＧ：ＧＨ＝１：２になるそうです。

以上が、三角形の4心です。