（３０）円についての諸定理

（１）円周角の定理

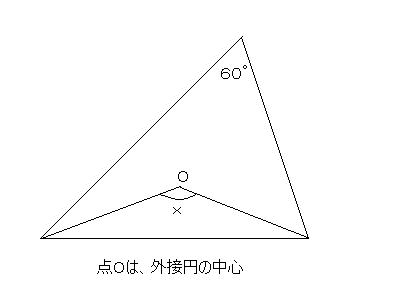
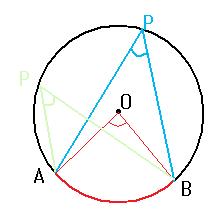弧ＡＢ以外の円周上の点をＰとすると、∠ＡＰＢは、中心角∠ＡＯＢの半分になる。
これが、円周角の定理です。
この定理は教科書に載っていますね。

以下は、知らなくても問題は解くことができますが、知っていると便利な定理。

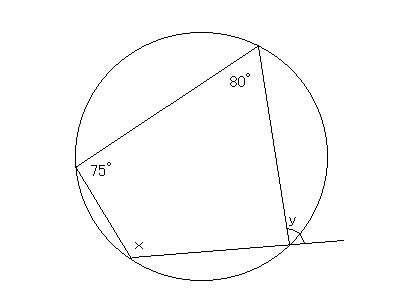
（２）円に内接する四角形の定理

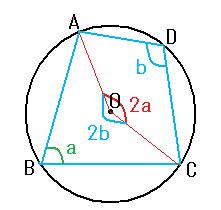
円に内接する四角形ＡＢＣＤがあって、∠Ｂ＝ａ、∠Ｄ＝ｂとすると、
円周角の定理から、中心角は、それぞれ２ａ、２ｂとなります。
よって、２ａ＋２ｂ＝３６０°　つまり、ａ＋ｂ＝１８０°
つまり、円に内接する四角形の向かい合う内角の和は１８０°
これが、円に内接する四角形の定理です。

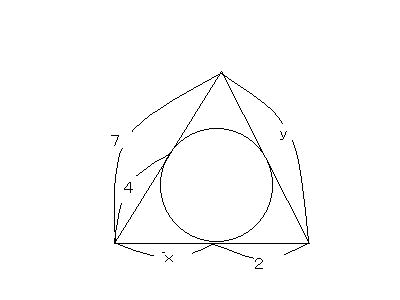
（３）接線についての定理

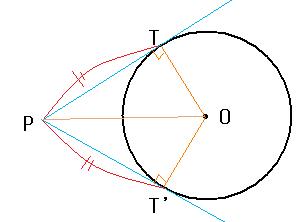
円外の点Ｐから、円Ｏに接線ＰＴ、ＰＴ’を引くと、
△ＰＴＯ≡△ＰＴ’Ｏですよね。ゆおって、ＰＴ＝ＰＴ’
つまり、円外の点から円に引いた２本の接線の長さは等しい。
これが、接線についての定理です。

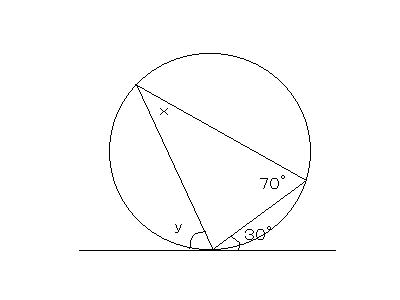
（４）接弦定理（接線と弦の作る角についての定理）

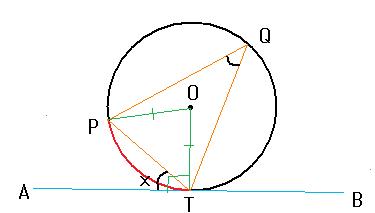
円Ｏの接線ＡＢと弦ＰＴの作る∠ＰＴＡ＝ｘ°とすると、
接線と接点を通る円の半径は垂直に交わるので、∠ＯＴＡ＝９０°－ｘ°＝∠ＯＰＴ
よって、∠ＰＯＴ＝１８０°－２（９０°－ｘ°）＝２ｘ°
円周角の定理より、∠ＰＱＴ＝ｘ°となり、∠ＰＴＡ＝∠ＰＱＴ
つまり、接線と弦の作る角は、その角の内部にある弧に対する円周角に等しい。
これが、接弦定理です。

以上が、円についての諸定理です。
では、練習問題にチャレンジしてみてください！