（２４）二次関数

（問１）次のグラフの頂点を求めなさい。
　　（１）ｙ＝ｘ２＋８ｘ＋１９　　　　（２）ｙ＝２ｘ２－１２ｘ＋１７

　ｙ＝（ｘ２＋８ｘ＋１６）＋３ 　　　ｙ＝２（ｘ２－６ｘ＋９）－１

　ｙ＝（ｘ＋４）２＋３ 　　　　　　　ｙ＝２（ｘ－３）２－１

　頂点は（－４，３） 　　　　　　　　頂点は、（３，－１）

ちなみに、２次方程式の解は、「２つある」、「１つ（重解）ある」、「解なし」の３通りありますよね。これは、

ａｘ２＋ｂｘ＋ｃ＝０の解は、 ｙ＝ａｘ２＋ｂｘ＋ｃ　と　ｙ＝０（ｘ軸）の連立方程式の解

と考えると、グラフ上ではっきりと確認できます。

例えば、

ｘ２＋２ｘ－８＝０　の解は、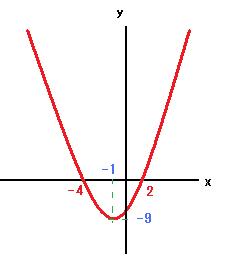
（ｘ＋４）（ｘ－２）＝０
ｘ＝－４，２
ですね。

ここで、ｙ＝ｘ２＋２ｘ－８とｙ＝０（ｘ軸）の連立方程式の解と考えると、
　ｙ＝ｘ２＋２ｘ－８のグラフは、
　ｙ＝（ｘ＋１）２－９　ですから、
　頂点は（－１、－９）で、
右のグラフのように、交点が２つあることが確認でき、そのｘ座標が、－４と２ということです。

次に、ｘ２－６ｘ＋９＝０　の解は、（ｘ－３）２＝０　で、　ｘ＝３　で解が１つです。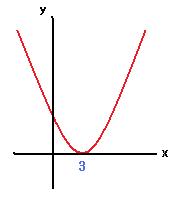

これも同様に、ｙ＝ｘ２－６ｘ＋９　と　ｙ＝０（ｘ軸）の連立方程式の解と考えると、
ｙ＝ｘ２－６ｘ＋９＝（ｘ－３）２＋０　ですから、
頂点は、（３，０）で、
右のグラフのように、交点が１つだけであることが確認でき、そのｘ座標が、３ということです。








最後に、ｘ２－４ｘ＋５＝０　の解はないはずです。（中学校レベルのお話）
これも同様に、ｙ＝ｘ２－４ｘ＋５　とｙ＝０（ｘ軸）の連立方程式の解と考えると、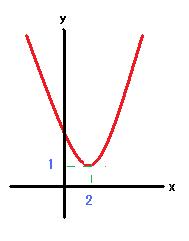
ｙ＝ｘ２－４ｘ＋５＝（ｘ－２）２＋１　ですから、
頂点は、（２，１）で、
右のグラフのように、交点がないことが確認できます。