（２４）二次関数

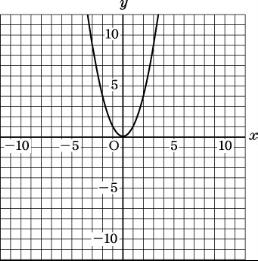
下のグラフは、ｙ＝ｘ２のグラフです。これに、ｙ＝ｘ２－４ｘ＋５　のグラフを書き加えてみてください。
とりあえず、ｘの値が、－２から５まで、調べてみれば、グラフの様子が分かるはずです。

ｘ	－２	－１	０	１	２	３	４	５
ｙ

ｘ＝－２とすると、ｙ＝（－２）２－４×（－２）＋５＝４＋８＋５＝１７
ｘ＝－１とすると、ｙ＝（－１）２－４×（－１）＋５＝１＋４＋５＝１０
ｘ＝０とすると、ｙ＝０２－４×０＋５＝０＋０＋５＝５
ｘ＝１とすると、ｙ＝１２－４×１＋５＝１－４＋５＝２
ｘ＝２とすると、ｙ＝２２－４×２＋５＝４－８＋５＝１
ｘ＝３とすると、ｙ＝３２－４×３＋５＝９－１２＋５＝２
ｘ＝４とすると、ｙ＝４２－４×４＋５＝１６－１６＋５＝５
ｘ＝５とすると、ｙ＝５２－４×５＋５＝２５－２０＋５＝１０

ですから、

ｘ	－２	－１	０	１	２	３	４	５
ｙ	１７	１０	５	２	１	２	５	１０

となり、グラフは、



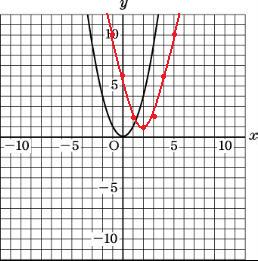
と言うようになります。
ｙ＝ｘ２(黒）と、ｙ＝ｘ２－４ｘ＋５(赤）のグラフを見比べると、グラフの違いは頂点の通る場所が、ｙ＝ｘ２(黒）は原点ですが、ｙ＝ｘ２－４ｘ＋５(赤）は原点ではなく、点（２，１）と言うことだけです。
これは、「比例」と「一次関数」の違いのときと同じですよね。
同じように、
ｙ＝ｘ２(黒）は、「２乗に比例する関数」
ｙ＝ｘ２－４ｘ＋５(赤）は、「二次関数」と呼びます。

と言うことで、、「二次関数」のグラフは、頂点の位置が分かれば、あとは、「２乗に比例する関数」のときと同じ手順で書けるということになります。
頂点の求め方は、

ｙ＝ｘ２－４ｘ＋５

ｙ＝（ｘ２－４ｘ＋４）＋１

ｙ＝（ｘ－２）２＋１

　ｘ＝２のとき、ｙは最小値１となるので、頂点は（２，１）と分かります。

では、練習問題です。

（問１）次のグラフの頂点を求めなさい。
　　（１）ｙ＝ｘ２＋８ｘ＋１９　　　　（２）ｙ＝２ｘ２－１２ｘ＋１７