（２３）点と直線の距離を求める

2直線の垂直条件を利用すると、下のような点と直線の距離を求める問題を解くことができます。

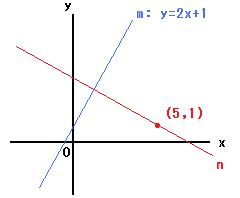
（問題）直線ｍ： ｙ＝２ｘ＋１と点（５，１）との距離を求めなさい。



(求め方）
点（５，１）を通って直線ｍと垂直な直線ｎを考えます。
直線ｍの傾きが２で、ｍ⊥ｎだから、直線ｎの傾きは、-0.5となります。
よって、直線ｎは、傾き-0.5で、点（５，１）を通る直線だから、
ｙ－１＝-0.5（ｘ－５）
ｙ－１＝-0.5ｘ＋2.5
　　 ｙ＝-0.5ｘ+3.5

次に、直線ｍ、ｎの交点の座標は、連立方程式
ｙ＝２ｘ＋１

ｙ＝－0.5ｘ+3.5　　を解いて

ｘ＝１，ｙ＝３で、（１，３）となります。

よって、（５，１）と（１，３）の距離Ｌを三平方の定理で求めると、

Ｌ２＝（５－１）２＋（３－１）２

Ｌ２＝１６＋４

Ｌ２＝２０

Ｌ＝２√５

答　２√５