傾きがaで、点(x1,y1)を通る直線の式を華麗に求める公式を作ります。
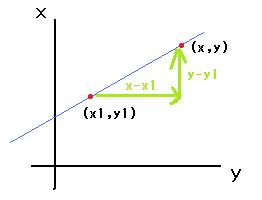
まず、この直線上のすべての点(x、y)について考えると、傾きがaになることから、
x-x1
a=---------
y-y1
ですよね。
ということで、y-y1=a(x-x1)
つまり、
傾きaで、点(x1、y1)を通る直線の方程式
y-y1=a(x-x1) |
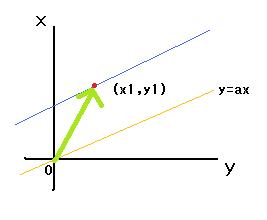
また、この直線は、直線 y=ax を
x軸方向にx1、y軸方向にy1だけ平行移動したグラフ
と考えることができます。これも大切な考えです。
では、この考えで、一次関数の式を求めてみましょう。
(例)傾き3で、点(1,2)を通る直線
y-2=3(x-1)
y-2=3x-3
y=3x-1
では、次の練習問題に挑戦してみてください。
(問)次の直線の式を求めなさい。
(1)傾き2で、点(1、3)を通る直線
(2)傾き-3で、点(2、-1)を通る直線



