（２２）一次関数の式をすばやく作る

（問）次の直線の式を求めなさい。

（１）傾き２で、点（１、３）を通る直線
　　　ｙ－３＝２（ｘ－１）
　　　ｙ－３＝２ｘ－２
　　　　　ｙ＝２ｘ＋１


　（２）傾き－３で、点（２、－１）を通る直線

　　　　　ｙ＋１＝－３（ｘ－２）
　　　　　ｙ＋１＝－３ｘ＋６
　　　　　　　 ｙ＝－３ｘ＋５

さて、ｙ軸のａを通り、ｘ軸に平行な直線の式は、
傾き０の直線の式ですから、ｙ＝ａ

ちなみに、

ｘ軸のａを通り、ｙ軸に平行な直線の式は、
ｘとｙを入れ替えただけなので、ｘ＝ａ
となります。


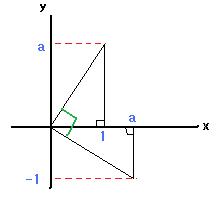
ここで、２直線の平行条件は、傾きが同じことですが、垂直条件は、下の図のように、直角を作る２辺の長さが１とａである合同な直角三角形を下のように組み合わせると、原点のところで、直角になることから、
原点で垂直に交わる2直線の傾きの積は、　ａ×（-1/ａ）＝－１
つまり、垂直な２直線の傾きの積は、－１となります。

よって、

＜２直線の垂直条件＞ 直線ｍ：ｙ＝ａ1ｘ＋ｂ1と直線ｎ：ｙ＝ａ２ｘ＋ｂ２　が、垂直ならば、　　　　　　　　　　　　　ａ1×ａ２＝－１

と、なります。