（１４）円周率にまつわる話

（解答）
半径がａである円に内接する正１２角形を考え、この一辺をｂとすると、
この一辺ｂと２つの半径で囲まれてできる三角形は、
３０°、７５°、７５°の３つの角を持つ二等辺三角形です。


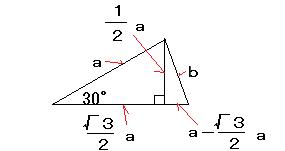
すると、ｂ^２＝（ａ/2）^２＋｛（２－√３ａ）/2｝^２
　　　　　ｂ^２＝（２－√３）ａ^２
ここで、円周＞正12角形の周だから、
　　　　２ａπ＞１２ｂ
　　　　　　ａπ＞６ｂ
　　　　　ａ^２π^２＞３６ｂ^２
　　　　　ａ^２π^２＞３６（２－√３）ａ^２
　　　　　　　π^２＞３６（２－√３）
ここで、√３＜１．７４だから、２－√３＞２－１．７４＝０．２６
なので、　π^２＞３６×０．２６＝９．３６＞９．３０２５＝（３．０５）^２
よって、π＞３．０５