where, all vectors u, v, a, and b are unit vectors.
Top page (correct Bohr model including the two-electron atoms)
Bohr model vs. Bell inequality violation (CHSH).
The violation of Bell inequality in Aspect's experiment showed that local realism ( local hidden-variables ) was denied.
Later, Leggett suggested the non-local hidden-variable theories (= non-local realism), which can violate Bell inequality (CHSH-type).
But his Leggett-type inequality has also been denied by the recent experiments (Nature 446,871,(2007)).
The important point is that these experiments use the "unreal" photon particles.
If we use the simple electromagnetic wave model instead of the photon particles, we can express the local-realism model, which is compatible with the quantum-mechanical experimental results. ( See this page ! )
By the way, what is this Leggett-type inequality ?
His theory is really one of the nonlocal realistic ones ?
Actually, Leggett-type model has some fatal defects.
Here we explain these defects of this model in detail.
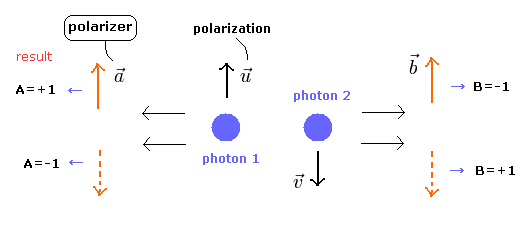
First we suppose the two entangled photons (1 and 2) with the antiparallel polarization axes ( u in 1, v in 2, v = -u )
Fig.1 Entangled photons and polarizers.

where, all vectors u, v, a, and b are unit vectors.
The photon 1 goes toward the polarizer a, and the photon 2 goes toward the polarizer b.
If the polarizer a and polarization axis of u are parallel ( a = u ), the trasmitted photon amplitute A (not probability density) becomes A= +1.
(If they are "antiparallel", A becomes -1. )
According to Malus' law, the transmitted light amplitute is cosθ (θ is the angle between polarization axis of photon and polarizer).
In Leggett's model, the nonlocal hidden variable (= λ) is allowed.
This means that the information of polarizer a is "superluminally" transmitted to the polarizer b !
But it satisfies "realism" !
Is it really possible ?
In Leggett's model, the result A in the polarizer a becomes, as follows,
(Eq.1)
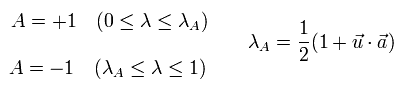
For example, when the vectors u and a are parallel to each other, the inner product of u and a becomes +1.
So λA is 1, which means the result A always becomes +1.
If the vectors u and a are antiparallel, the inner product of u and a becomes -1.
So λA is 0, which means the result A always becomes -1.
And the result B in the polarizer b is,
(Eq.2)
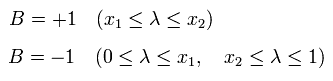
where these x1 and x2 satisfy the next condition,
(Eq.3)
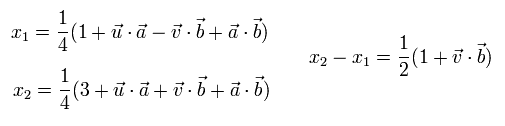
Eq.3 means that the result B in the polarizer b is "superluminally" influenced by the result A (= x contains the inner product u and a).
Here the polarization axes of entangled photons 1 and 2 are antiparallel to each other, as follows,
(Eq.4)
Using this strange nonlocal variable λ , the average results of A and B becomes,
(Eq.5)
Surprisingly, as shown in Eq.5, Leggett's model satisfies Malus's law in each photon.
Each photon with definite polarization axis (=realism) satisfies Malus's law independently, but they violate CHSH-type Bell inequality ! (Eq.6)
Is it really possible !?
( About the detailed explanation of CHSH-type inequality, see this page. )
( Eq.6. the average result of a combination of A and B )
For example, when 0 < λ < x1 in the first term, AB = +1 (=A) × -1 (=B) = -1 (See Eq.1 and Eq.2 .)
Eq.6 means that the instant the photon 1 has passed through the polarizer a, the polarization axis of the photon 2 becomes the same (= antiparallel) as the polarizer a. (= Entanglement, see also this page. )
Actually, these surprising phenomena are caused by hiding some defects of Leggett's model.
First, if the condition of Eq.2 is satisfied, x1 and x2 must satisfy the next condition,
(Eq.7)
The restriction of Eq.7 is the same as Eq.8,
(Eq.8)
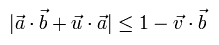
And Eq 6 contains the next restriction,
(Eq.9)
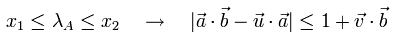
Combining Eq.8 and Eq.9, Leggett model must satisfy the next important condition,
(Eq.10)
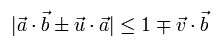
Eq.10 is the origin of the illusion in the nonlocal realistic Leggett's model.
For example, when the directions of the polarizers a and b are the same, as follows,
(Eq.11)
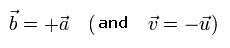
x1 and x2 become,
(Eq.12)
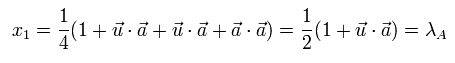
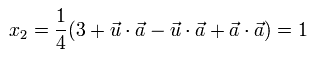
From Eq.1, Eq.2 and Eq.12, the results of A and B are as follows, (depending on the common nonlocal parameter λ)
(Eq.13)
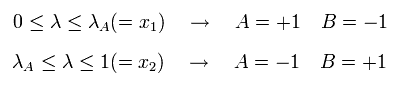
According to Eq.13, the results A and B are always opposite (=antiparallel), which means the entanglement of photon 1 and 2 is occurring.
The case of Eq.13 corresponds to Fig.2 of our electromagnetic wave model.
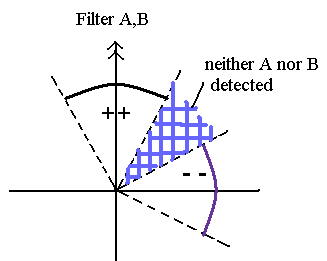
Fig.2. the electromagnetic wave model. (= local and realistic model)
(here the probability density is used instead of amplitude, but the meanings of them are the same.)
The photons 1, and 2 are denoted by photon A and B, and polarizers a and b are denoted by Filter A and B here.
This figure shows the case in which the angles ( = the directions of the arrows) of the polarizing filters A (=a) and B (=b) are the same ( = 0 degree).
As I said, the photon 1 (=A) and 2 (=B) have the opposite ( = antiparallel) polarization axes. So in this case, when the photon 1 passes through the polarizer a, the photon 2 always passes through the polarizer b, too. ( = cos2 0 = 1 )
When the polarization axis of the photons 1 ( this axis is the same (=antiparallel) as the photon 2), points toward ( ++ ) of this figure, both the photons 1 and 2 pass each filter, and are detected as "photon particles"
But when the polarization axis of the photon 1( = photon 2) points toward the blue part of this figure, the transmitted (or reflected) light intensities of both the photons 1 and 2 are below the detection threshold. So neither photon 1 nor 2 can be detected as a "photon particle" by the detector (this case is not used even in calculating the detection efficiency).
And when the polarization axis of the photon points toward the ( -- ) of this figure, both the photons 1 and 2 are reflected by the filters enough to be detected as "photon particles".
So in this case, the "illusion" of the entanglement of these pair photons is occurring, which can be explained by our electromagnetic wave model.
How about the next case of Fig. 3 ?
(Fig. 3)
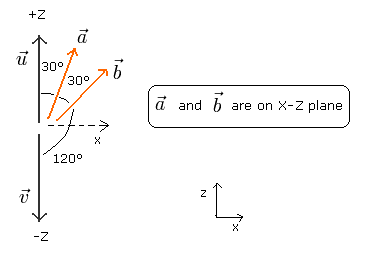
where the angle between the polarization axis u of photon 1 and the polarizer a is 30 degrees, and the angle between the polarization axis v of photon 2 and the polarizer b is 120 degrees.
Substituing these vectors of Fig.3 into Eq.8, the next wrong inequality is gotten,
(Eq.14)
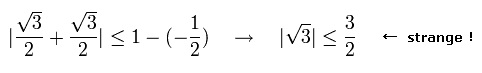
Eq.14 is wrong !
This is the origin of the illusion in Leggett's model.
In some angles, Leggett's theory is broken, which means the nonlocal realism is denied in some conditions.
Of course, as shown in this page, our electromagnetic wave model can explain this condition of Fig. 3 completely, though it is "local realistic" model.
Fig. 4. The electromagnetic wave model. (= local and realistic model.)
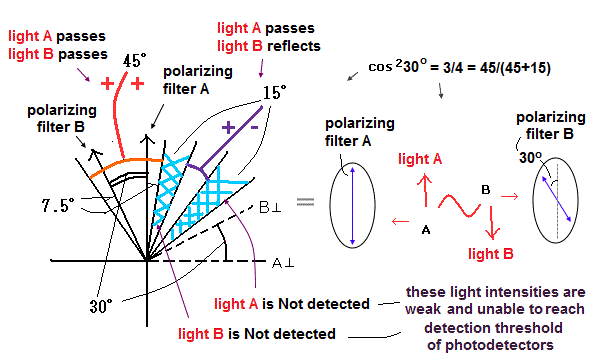
Red parts (+ +) --- Both photon 1 and 2 pass the filters and detected.
Purple parts (+ -) --- Photon 1 passes and photon 2 is reflected by the filters and both are detected as photons
Shaded parts (light blue) --- Only 1 (pass) or 2 (reflect) can be detected as a photon. (= this case is not used as a correct experimental result.)
Basically, if the next condition of Eq.15 is satisfied, Leggett's model doesn't contradict the restriction of Eq.10.
(Eq.15)
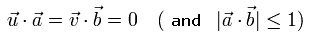
(Try substituting Eq.15 into Eq.10 !)
When the condition of Eq.15 is satisfied, the direction of each vector becomes as follows,
(Fig. 5)
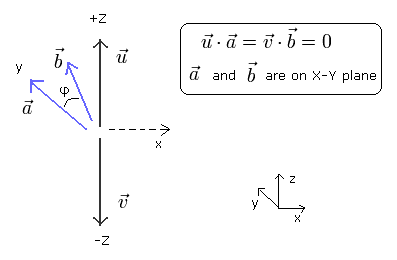
where polarizers a and b are on the x-y plane, so they are perpendicular to vectors u and v of photons.
In Fig.5, in any arbitrary angle (φ) between a and b, Leggett's model can violate the CHSH-type Bell inequality, because Eq.10 is always satisfied.
But the situation of Fig.5 is very unnatural, I think.
Next we derive the Leggett-type ineuqality.
For any mesurement results (A= ± 1, B= ± 1), the following identity is satisfied.
(Eq.16)
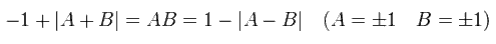
The average results of Eq.16 is,
(Eq.17)
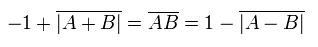
And the next inequality can be gotten,
(Eq.18)
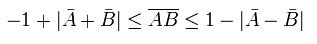
Here we use Malus' law in each photon with "definite" polarization (=realism).
(Eq.19)
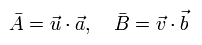
As I said above, this replacement is not consistent with the quantum mechanical results in some angle φ.
Substituting Eq.19 into Eq.18,
(Eq.20)
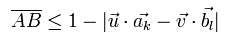
where k and l means polarizer's number. (We need several different polarizers in this experiment).
So the average result of various polarization axes in photons u and v is,
(Eq.21)
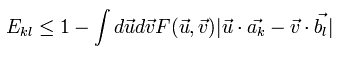
As shown in Fig.5 and Eq.15, if we take the polarizes which exist in only one plane, Leggett's model can violate CHSH-type Bell inequality.
So we need to use the polarizers which exist in different planes (x-y and x-z) as follows,
Fig. 6. Three-dimensional polarizers in Poincare sphere.
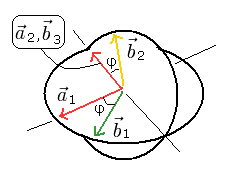
where the polarizer a2 is equal to b3
The angle between polarizers a1 and b1 is φ
And the angle between a2 and b2 is φ, too.
(a1 and b1 are in the x-y plane, and a2 and b2 are in the x-z plane.)
If we take the polarizers of Fig.6, the sum of four Ekl of Eq.21 become as follows,
(We need to do long calculation, which is explained in detail in this paper (arXiv 0704.2529v2).)
( Eq.22. Leggett-type inequality. )
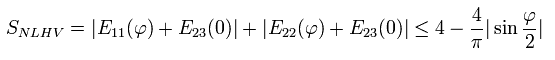
If we take the quantum mechanical correlation, each Ekl of Fig.6 becomes as follows,
(Eq.23)
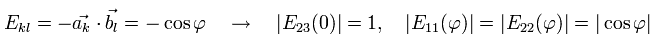
So the Leggett inequality of Eq.22 changes to Eq.24 in the quantum mechanical condition,
(Eq.24)
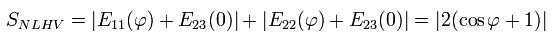
In some angle φ, Leggett inequality of Eq.22 is violated in the experiments.
(The experimental results are the same as Eq.24.)
The difference between Leggett inequality of Eq.22 and the quantum mechanical equation of Eq.24 is caused by the replacement of Eq.19 (=realism).
As I said above, if we try to take the realism of Eq.5 and Eq.19, in which photons have "definite" polarizations,
the very strict restriction of Eq.10 must be satisfied.
This restriction of Eq.10 is too strict to be satisfied in some angle φ. (For example, Fig.3).
As a result, Leggett-type inequality (Eq.22) is not equal to the quantum mechanical equation (Eq.24).
From the beginning, "incomplete" Leggett model tried to do the impossible thing (= entanglement + realism + photon).
Recently, using the orbital angular momentum states (which is similar to the polarization) of the light,
Leggett-type inequality proved to be violated.
(New Journal of Physics 12 (2010) 123007).
This means nonlocal realistic models including de Broglie Bohm's theory are denied.
So they insist that the quantum mechanics has showed this world has NO reality !
This means that our world is a illusion !?
These strange results are caused by the misunderstanding in which photons are considered to be "real" things.
If a photon is a "real" particle, single photon can interfere with itself as shown in Fig.7 ??
Fig.7. Mach-Zehnder interferometer
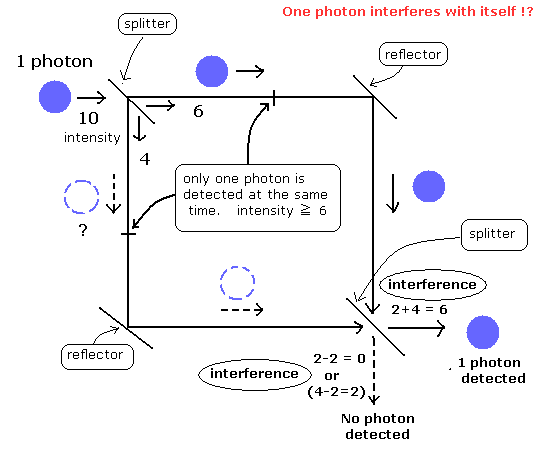
As shown in this page, our electromagnetic wave model can explain this single photon interference correctly and naturally.
If a photon is a "real" particle, single photon can be divided into two ??
Even if single photon can be "divided", the interference itself is based on the electromagnetic wave nature.
Before considering the "complicated" entanglement experiments, the photon itself has no reality.
This fact leads to the illusion that the entanglement experiments have denied the local (and nonlocal) realistic world.
Instead of insisting "Quantum physics says goodbye to reality", we had better say goodbye to quantum mechanics.

2010/12/31 updated. Feel free to link to this site.