第五回

第五回
2002/11/15

『シミュレーション概論』　講義メモ No.5 　　　＜課題３＞
数値積分（定積分）

　ここでは，１変数の連続関数の定積分を数値的に求めることを扱う。一般に微分方程式の解を数値的に求めることも数値積分ということになるが，これは後で扱う。

　不定積分が代数関数や超越関数（三角関数，対数関数，指数関数など）で与えられる場合は，定積分を求めるのにわざわざ数値積分する必要はない。そうでない場合でも，よく出てくるものについては定積分が特殊関数として定義され（誤差関数，楕円関数など），市販の数学ライブラリに納められていたり，数値計算のデータブックで優秀な近似式が見つかることも多い。

　しかしながら，比較的性質の良い関数なら，変形してライブラリを探したりするよりは，自分でプログラムを組んでしまう方が手っ取り早く，計算時間をそれほど気にしなくても，実用的には十分な精度で数値解が得られるものである。

（１）台形公式

　定積分

b S = ∫ f(x) dx a
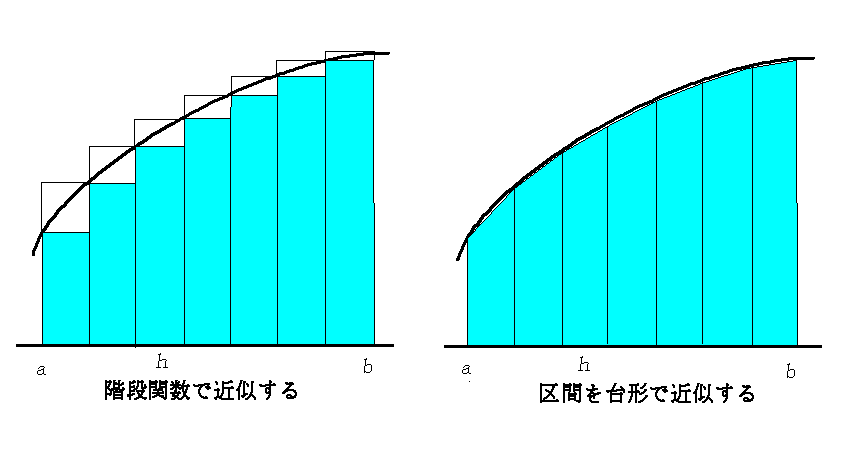
を求めるとする。高校の教科書に出てくる定積分の定義どおり，図のように区間 (a,b) を幅 h = (b-a)/N の区間に N 等分して階段状の面積を求め，N をできるだけ大きくすればよい，と考えたくなるであろう。

　しかしながら階段ではなく，各区間で関数を右図のように直線で近似して台形の面積の和を求めることにすれば，プログラム上は以下のようにほんのわずかな修正で精度は格段に上がる。N=100 等分した場合であれば，前者が 1/100 の誤差があるのに対して，台形公式ではじつに 1/10000，すなわち10000等分した場合に相当する精度が得られる。

プログラムは，階段で求める場合

s = 0.0 DO i = 0, N-1 !　右端（または左端）は加えない。 s = s + f(a+i*h) END DO s = s*h

に対して，台形公式では

s = 0.5 * ( f(a) + f(b) ) ! b = a+N*h である。 DO i = 1, N-1 s = s + f(a+i*h) END DO s = s*h

であり，両端を1/2の重みで加えるだけで手順は殆ど差はない。

　理由を考えてみよう。階段で近似する場合の誤差は，図のような単調関数の場合，明らかに両端の柱部分である。このことから一般に N 等分した場合の近似値 s_N と真の値 s との差は

| s_N - s | ＜ (f_max - f_min) h　　　　　f_max，f_min は，(a,b) での最大値と最小値

であると考えてよい。

　台形公式の場合，左端の区間 (a,a+h) を考えてみよう。Taylor展開を用いれば，真の積分値は

a+h ∫ f(x) dx = f(a) h + [f'(a)/2] h^2 + [f''(a)/6] h^3 + ... a
である。同様に台形の面積は

[ f(a) + f(a+h) ] h / 2 = f(a) h + [f'(a)/2] h^2 + [f''(a)/4] h^3 + ...
であり，その差は

[f''(a)/12] h^3 + ...
である。平均値の定理を用いれば，この式の a の代わりに (a,a+h) の間の適当な値を採用すれば　+.... の無い形で表すことが可能である。したがって

| s_N - s | ＜ [f''_max/12] (b-a) h^2
としてよく，誤差は 1/N² の程度になる。

　問題は「ノートNo.２」で述べた「丸め誤差の蓄積」である。例えば，定積分

1 ∫ 4/(1 + x^2) dx = π 0
を，区間 (0,1) を N = 2^k (k=3,20) 等分して台形公式で求めてみよう：

＜Fortranプログラム＞

INTEGER :: j, k, N REAL :: h, s, x, f ! DO k = 3, 20 N = 2**k h = 1.0/N s = 0.5*( f(0.0) + f(1.0) ) DO j = 1, N-1 x = j*h s = s + f(x) END DO s = s*h PRINT "(I10, F12.7, F12.6)", N, s, s/3.14159265 END DO END ! 被積分関数の定義部分 REAL FUNCTION f(x) REAL :: x f = 4.0/(1.0 + x*x) END FUNCTION
＜結果＞　（ただし最適化なし）
N s s/Pi 8 3.1389885 0.999171 16 3.1409416 0.999793 32 3.1414294 0.999948 64 3.1415517 0.999987 128 3.1415832 0.999997 256 3.1415906 0.999999 512 3.1415911 0.999999 1024 3.1415923 1.000000 2048 3.1415927 1.000000 4096 3.1415932 1.000000 8192 3.1415925 1.000000 16384 3.1415939 1.000000 32768 3.1415918 1.000000 65536 3.1415901 0.999999 131072 3.1415541 0.999988 262144 3.1415567 0.999989 524288 3.1412396 0.999888 1048576 3.1404257 0.999628

　区分数をむやみに増やしても，何の役にもたたず，かえって誤差が増えていることがわかるだろう。

　この区分数を２のｎ乗の形にとることは，次のシンプソン公式との関係で意味がある。

（２）シンプソン公式

　連続する３点を放物線で近似することにより，さらに精度はよくなる。

３点 (p-h,f(p-h)), (p,f(p)), (p+h, f(p+h)) を通る放物線は

g(x) = A(x-p)^2 + B(x-p) + C A=[f(x-p)-2f(p)+f(x+p)]/2h^2, B=[f(p+h)-f(p-h)]/2h, C = f(p)
と表される。これより積分の近似値は

p+h ∫ g(x) dx = 2Ah^3/3 + 2Ch = (h/3)[f(p-h)+4f(p)+f(p+h)] p-h
Taylor展開を用いれば

= 2h [f(p) + (f"(p)/6) h^2 + (f""(p)/72) h^4 + ...]
となる。

　一方，真の積分値は

p+h ∫ f(x) dx = 2h [f(p) + (f"(p)/6) h^2 + (f""(p)/120) h^4 + ...] p-h
となり，第２項まで一致するから誤差は h⁵ 程度，区間全体としては (b-a)/2h 倍して

　　　　　真の値からの誤差＜ [f""_max/180] (b-a) h^4
と考えることができる。

　プログラムはやや複雑になる。両端と奇数番目，偶数番目の点で重みが 1/3, 4/3, 2/3, 4/3, 2/3, ...,4/3, 1/3 と異なるからである。（関数の定義部分は前出のプログラムと同じだから省略した。）

INTEGER :: j, k, N 1 4 1 1 4 1 1 4 1 ... REAL :: h, s, x, f 1 4 1 1 4 1 ..... ! ----------------------- DO k = 3, 20 1 4 2 4 2 4 2 4 2 4 .....2 4 1 N = 2**k h = 1.0/N s = f(0.0) + f(1.0) ! 両端は重み１（つまり1/3）！ DO j = 1, N-1, 2 ! 奇数項は重み４（同　4/3） x = j*h s = s + 4.0*f(x) END DO ！ DO j = 2, N-1, 2 ! 偶数項は重み２（同　2/3） x = j*h s = s + 2.0*f(x) END DO ！ s = s*h/3.0 ! 最後に h/3 倍する。 ! PRINT "(I10, F12.7, F12.6)", N, s, s/3.14159265 END DO END N s s/Pi 8 3.1415927 1.000000 16 3.1415927 1.000000 32 3.1415927 1.000000 64 3.1415932 1.000000 128 3.1415930 1.000000 256 3.1415913 1.000000 512 3.1415930 1.000000 1024 3.1415930 1.000000 2048 3.1415913 1.000000 4096 3.1415951 1.000001 8192 3.1415949 1.000001 16384 3.1415930 1.000000 32768 3.1415961 1.000001 65536 3.1416073 1.000005 131072 3.1416357 1.000014 262144 3.1414626 0.999959 524288 3.1418412 1.000079 1048576 3.1398065 0.999431
　結果を見てわかるように，このような滑らかな関数であれば，有効数字６桁の範囲でなら，実に８等分でも十分なのである。

　単一の定積分を求めるだけなら，台形公式でも十分役立つ。アルゴリズムを暗記できるくらいにプログラムが簡単だからである。しかしながら大きなプログラムの中で定積分を繰り返し何度も必要とする場合にはシンプソン公式が有効である。

（３）台形公式とシンプソン公式

　先にふれたように，台形公式で N=2^k 等分の方法をとる場合は，次のようにして 2^k+1 等分公式あるいはシンプソン公式と関連づけることができる。ただし上の例ではプログラムを分かりやすくするため，これを使ってはいない。

2^k 等分公式 1/2 1 1 1 1 1 ...... 1 1/2 ＋）中間点の和 1 1 1 1 1 1 ...... 1 ------------------------------------------------------------------ 2^(k+1) 公式 1/2 1 1 1 1 1 1 1 1 1 1 ..........1 1/2
前の次数の結果に，中間点での関数値だけ加えていけば次の次数の結果が得られる。こうして計算して途中の結果も出力すれば，結果的には同じ計算回数でもって近似が上がっていく（あるいは次数が高すぎると悪くなっていく）経過を見ることができる。

　実は，この中間の値を加える際に２倍とし，結果を2/3倍するだけで，シンプソン公式になる：
2^k 公式 1/2 1 1 1 1 1 .......1/2 ＋）中間点の和 2 2 2 2 2 ..... 2 重み２ ------------------------------------------------------------------ シンプソン 1/2 2 1 2 1 2 1 2 1 ........ 2 1/2 ×(2/3) 1/3 4/3 2/3 4/3 2/3 4/3 ...............2/3 4/3 1/3
　ここでもまた，わずかな変更で精度が飛躍的に向上する例に出会ったということだ。

＜課題３－１＞
　上で説明した方法を用いて，区分数 N=2^k (k=2～20) について，台形公式とシンプソン公式による定積分を同時に求め，各 k について両者を並べて出力するプログラムを作成せよ。関数は，ここで用いたものでもよいし，そのほか予め定積分の分かっているものがよい。［Visual Fortran を使用する場合は，コンパイルの際に実数処理最適化を無効にするオプション「 -Op 」をつけてコンパイルすること。］　（参考結果）

　なお，N=2^k 等分の台形公式の場合，計算操作数は約２倍になるが，次のようにして配列を用いて隣り合う同程度の大きさの項を２つずつ集めていくことにより，丸め誤差の蓄積を最小限に押さえることが可能である。上の方法で中間点の値の和を求める時にも利用できる。（注：中間点の数は 2^k である。）

s(0) = 0.5*(f(a)+f(b)) --| | => s(0) --| s(1) = f(a+h) --| | | => s(0) s(2) = f(a+2*h) --| | | => s(1) --| s(3) = f(a+3*h) --| ........ ........ ........ ........ ........ ........ ........ ........ ........ ........ | => s(2^(k-2)-1) s(2^k-2) = f(a+(2^k-2)*h) --| | | => s(2^(k-1)-1)--| s(2^k-1) = f(a+(2^k-1)*h) --|

　ここで紹介したプログラム例や実行例では，区分数を異様に大きくとってある。これはあくまでも計算機の誤差の特徴や実数計算の最適化を理解してもらうためであって，実際にはこんな計算を行うことは愚かであり，結果としてほしい精度を得るのに必要最小限の区分数を用いればよい。

（４）ロンバーグ公式

　倍精度（有効数字15桁）で結果を得たいときには，原理的にはシンプソン公式でも1000～5000等分くらいの区分数が必要である。（倍精度実行例）　そこで，さらに高次の多項式で近似することが考えられよう。この講義の目的からすると微に入りすぎるかもしれないが，数値計算においてはこのようなさまざまな工夫－－しかもアルゴリズムとしてはマイナーな改良－－が行われていることだけは知っておいて欲しい。

　台形公式とシンプソン公式の関係は次のように書くこともできる。

2^k等分台形公式 = h/2 h h h h ....... h h h/2 ×(4/3) +) 2^(k-1)等分公式 = 2h/2 2h 2h ....... 2h 2h/2 ×(-1/3) ----------------------------------------------------------------------- シンプソン公式 h/3 4h/3 2h/3 4h/3 2h/3 ....... 2h/3 4h/3 h/3
これは以下のように説明される。区分幅 h = (b-a)/2^k の台形公式の結果を S(0, k) とすると，真の積分値 I との誤差は

S(0,k) - I = [(f'(b)-f'(a))/12] h^2 - [(f'''(b)-f'''(a))/720] h^4 + ... = [..] h^2 - [....] h^4 + [......] h^6 - ...
と展開される（オイラー-マクローリンの公式）。ここでは右辺の展開係数の具体的な形を気にすることはない。この公式を区分数が半分，すなわち区分幅が２倍の 2h の場合に適用すれば

S(0,k-1) - I = 4 [..] h^2 - 16 [....] h^4 + 64 [......] h^6 - ...
となることを用いて，S(0, k) と S(0, k-1) の重みつき平均

S(1,k) = [ 4 S(0,k) - S(0,k-1) ] / 3
を作るとシンプソン公式であり，先頭の h² の項を消すことができて

S(1,k) - I = 4 [....] h^4 - 20 [......] h^6 + 84 [........] h^8 - ...
となり近似の次数が向上する。区分幅が２倍のとき，先頭の項は今度は 2⁴ 倍になる。そこで漸化式

S(m,k) = [ 4^m S(m-1,k) - S(m-1,k-1) ] / [ 4^m - 1 ]
により次々に高次の公式を生成すれば h の最低次の項を次々に消すことができて，m次の近似式では誤差は h^2m+2 程度となる。これは，関数を 2^m次多項式で近似することに相当し，区分数は 2^k≧2^m すなわち k≧m でなければならない。高次の多項式を用いて補間近似を行う公式の最も分かりやすい例であろう。

　したがって，最初から区分数を 2^p と決めた場合には，まず N = 1, 2, 4, 8, ..., 2^p 区分の台形公式による値, S(0, 0), S(0, 1), ..., S(0, p-1), S(0, p) を求めておき，せっかくそこまで計算したのであれば，次に上の漸化式を用いて S(p, p) まで求めれば，計算操作をさほど増やすことなく与えられた区分数において原理的には最良の近似を得ることができる。（32等分の実行例）

＜課題３－２＞　ロンバーグの公式を用いてこの実行例を出力するプログラムを作成せよ。

（５）無限区間の積分

　積分区間が無限になる場合，あるいは区間は有限でも端（または内部のどこか）で関数が発散している場合や，関数そのものは発散しなくても微分が発散しているような場合，以上のようにはいかない。（√x を x=0 ～ x=1 で台形公式またはシンプソン公式で積分してみよ。思うようにはいかないであろう。）

　このような場合には，一般には変数変換によって特異性を除くことができれば，ここまで述べてきた方法を適用することができる。例えば (0, ∞) 間の積分

∞ I = ∫ f(x) dx　 0
は，変数変換 y = exp(-x) によって (0, 1) 間の積分

1 I = ∫ f(-log y)/y dy 0
に変換できて，f(-log y)/y が y=0 で特異的でなければ，これまでの方法が適用できる。

　あるいは，予め関数の漸近形が評価できる場合には，発散点を挟む狭い領域を除くとか積分区間を有限区間で近似した場合の誤差を評価することができるから，素朴にはこのようにして積分値を求めることも考えられよう。

　最後におそらく意外な事実をあげておこう。それは，（-∞，+∞）で解析的で積分が収束する場合，任意の区分幅 h の台形公式が正確な積分値を与えるということである。これは（４）で述べたオイラー-マクローリン公式を見れば予想できよう。被積分関数の任意の階数の導関数が x=±∞ で０でなければならないからである。

　この場合の台形公式は単に

+∞ I(h) = h ∑ f(j*h) j=-∞
であるが，実際にはもちろん有限和しか実行できず，どこかで打ち切らなければならない。この場合の誤差は，区分幅ではなく打ち切りから来るものの方が本質的である。関数の収束が十分に速い場合には，信じられないほどの粗さで驚くべき精度の結果が得られる。

　以下はガウス積分

1 +∞ I = ----------- ∫ exp(-x^2 /2) dx = 1 (2π)^(1/2) -∞
を区分幅 h = 0.0625, 0.125, 0.25, 0.5 で実行した結果である。打ち切り値を x=8 くらいにとっておけばよいということは，区分幅の値にほとんど依存していないことがわかるだろう。

　この事実を利用すれば，有限区間の積分であっても，変数変換により収束の速い関数の無限区間の積分に変換することによって，計算効率を上げることが考えられる（二重指数関数法）が，ここでは割愛する。（早川先生の講義ノート「４講」参照）

（付）数式処理プログラム（Ｍａｐｌｅ　Ｖ）

　メディアセンタ－のパソコンには，知らぬ間に数式処理プログラム「Ｍａｐｌｅ V」が導入されていた。単発の積分なら，ここで述べた拡張定積分も含めてやってのけてくれる。「プログラム」「Maple V」を立ち上げてから以下を実行してみよ。（＞はプロンプトで，行入力は　；（セミコロン）で閉じさせること。
      > int(1/(1+x^2), x);                不定積分
      > int(1/(1+x^2), x=0..1);　　       定積分　範囲は x = a..b と指定する。
      > int(1/(1+x^2), x=0..infinity);　　infinity は無限大の予約語
      > int((1-x^2)^(-1/2), x);
      > int((1-x^2)^(-1/2), x=0..1);
      > evalf(%);                         今の結果を実数値で評価

こんなものでもちゃんとやってくれる。（特殊関数のΓ関数になる）
      > int(x^(3/4)*exp(-x),x=0..infinity);
      > evalf(%);
最後は
      > quit;