垽昋導 埳嵅帰攇恄幮偺嶼妟
丂埳嵅帰攇恄幮(垽昋導)丂亂壝塱3 擭乮1850 擭乯 壴嶳嬥師榊 曭擺亃
乷尨暥乸丂丂丂丂丂 丂
崱桳擛殺捈慄忋嵹嶰妏懘撪愝擇幬梕撪摍堳嶰屄墑懘壓幬懘朤憓奜懘堎殺堦屄扅塢嶰妏柺擇廫悺栤奜堳宎擛壗
摎濰丂奜殺宎嬨悺楇楇桳婏 ( 嬨悺僛儘僛儘梋傝桳傝乯
丂楇
弍濰丂棫揤尦堦啜奜殺渓擇廫擵埲尭嬨廫嬨売镻忔奜殺渓撪尭昐幍廫堦屄镻忔奜殺渓壛堦昐堦廫幍屄墱擇廫幍屄丂丂丂丂丂
丂憡徚摼奐曽幃嶰忔曽擵摼彜埲尭堦屄屲暘镻埲彍彜忔嶰妏柺媦拞珀棪摼奜殺宎崌栤
乷尨暥偺梫栿乸
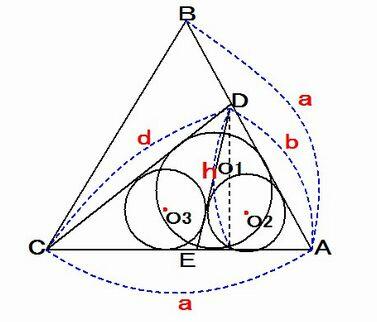
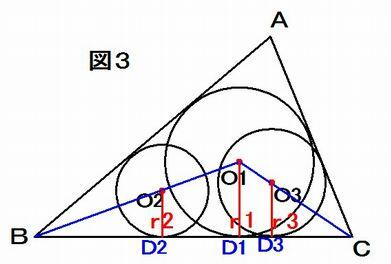
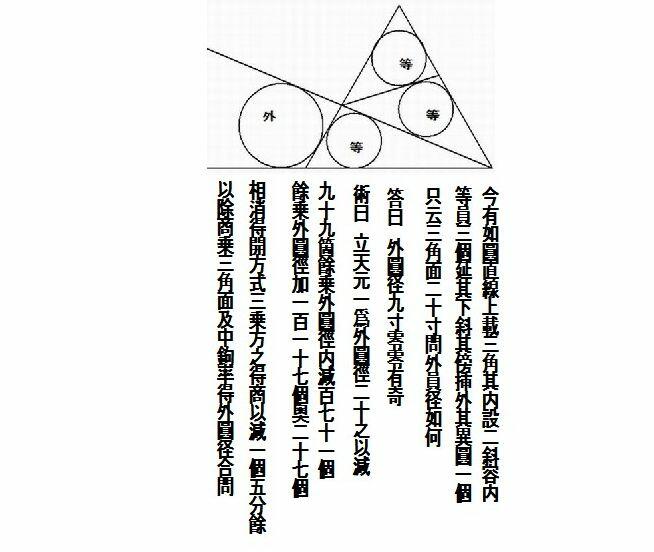
丂恾偺傛偆偵丄捈慄忋偵偁傞惓嶰妏宍傪2 杮偺慄暘偱暘偗偨嶰妏宍偵撪愙偡傞摍墌偑3 屄偁傝丄捈慄偲惓嶰妏宍媦傃
慄暘傪墑挿偟偨捈慄偵愙偡傞奜墌1 屄偑偁傞丅
惓嶰妏宍偺1 曈偺挿偝偑20 悺偺偲偒丄奜墌偺捈宎偺挿偝傪媮傔傛丅丂丂丂
丂
乷寁嶼曽朄乸丂丂丂
惓嶰妏宍撪偺3 摍墌偺敿宎傪媮傔傞丅
壓恾 偺傛偆偵丄惓嶰妏宍傪ABC丄2 杮偺慄暘傪DC丄DE丄3 屄偺摍墌偺拞怱傪O1丄O2丄O3 偲偟丄偦偺敿宎傪r 偲偡傞丅
4 慄暘AB丄AD丄AE丄DC 偺挿偝傪偦傟偧傟a丄b丄c丄d 偲偡傞丅
摍墌偺敿宎r 傪媮傔傞丅 ADC 偵
梋尫掕棟傪梡偄傞偲丄 d^2 = a^2 + b^2 - 2abCOS俙
COS俙 = COS60亱= 1/2 丒丒丒丒
嶰妏斾 嶲徠丂丂丂亪丂d^2 = a^2 + b^2 - ab 丒丒丒 幃嘆
撪愙墌O1 偲3 曈CD丄DB丄CB 偲偺愙揰傪偦傟偧傟 G丄H丄F 偲偡傞丅
偙偺偲偒丄O1HB 偼捈妏嶰妏宍偱佢O1BH = 30亱側偺偱丄 HB = 併3r 偱偁傞丅
捈妏嶰妏宍偺嵍抂偺妏搙偑30亱偺偲偒偺斾棪偼侾懳俀懳併俁乮懳曈a亖侾丄幬曈b亖俀丄掙曈c亖併俁乯
傑偨丄2HB =HB + BF = DB - DH + CB - CF = DB - GD + CB - CG = DB + CB - GD - CG =
(a - b) + a - d 傛傝丄 2a - b - d = 2併3r - d = 2併3r - 2a + b d = 2a - b - 2併3r 丒丒丒 幃嘇 偱偁傞
娭學幃傪梡偄偰丄惓嶰妏宍偺1 曈偺挿偝a 偲摍墌偺敿宎r 偺娭學幃傪摫偄偰傒傞丅
幃嘆偵幃嘇傪戙擖偟偰d 傪徚嫀偟惍棟偡傞丅丂丂丂(2a - b - 2併3r)^2 = a^2 + b^2 - ab 丂
岞幃丂(a-b-c)^2 = a2+b2+c2-2ac-2ab+2bc丂傛傝丂丂
(2a)^2 + b^2 + (2併3r)^2 - 2(2a)(2併3r) - 2(2a)b + 2b(2併3r) = a^2 + b^2 - ab
(2a)^2 + b^2 + (2併3r)^2 - 2(2a)(2併3r) - 2(2a)b + 2b(2併3r) - a^2 - b^2 + ab = 0
4a^2 + b^2 + 12r^2 - 8併3ar - 4ab + 4併3br - a^2 - b^2 + ab = 0
4a^2 - a^2 + b^2 - b^2 - 8併3ar - 4ab + ab + 4併3br + 12r^2 = 0
3a^2 - 3ab - 8併3ar + 4併3br + 12r^2 = 0 偲 側傞丅 b 偵偮偄偰夝偔丅
3a^2 - 3ab + 4併3br - 8併3ar + 12r^2 = 0 - 3ab + 4併3br = -3a^2+ 8併3ar - 12r^2
b(- 3a + 4併3r) = -3a^2+ 8併3ar - 12r^2 b = (-3a^2+ 8併3ar - 12r^2)乛(- 3a + 4併3r) 丂
b = 併3(-3a^2+ 8併3ar - 12r^2)乛併3(- 3a + 4併3r) = (-3併3a^2+ 24ar - 12併3r^2)乛(- 3併3a + 12r) 丂
= 3(-併3a^2 + 8ar - 4併3r^2)乛3(4r - 併3a) = -(-併3a^2 + 8ar - 4併3r^2)乛-(4r - 併3a) 丂
b = (併3a^2 - 8ar + 4併3r^2)乛(併3a - 4r) 丒丒丒 幃嘊
+
亂r1 傪媮傔傞亃
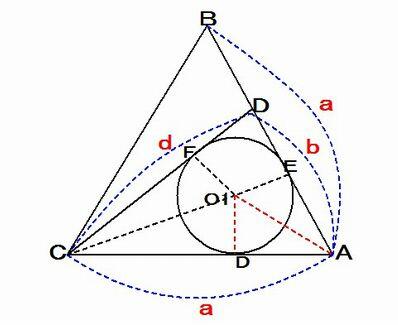
佢俙 偑60亱 偱偁傞ACD 偺撪愙墌O1 偺敿宎傪r1 偲偡傞丅曈CA丄AD丄DC 偺挿偝傪偦傟偧傟a丄倐丄倓 偲偡傞偲偒丄
師偺娭學幃偑惉傝棫偮丅 2併3r侾 = a + b - 倓 亪丂r1 = (a + b - 倓)乛2併3
乮徹柧乯撪愙墌O 偲3 曈CA丄AD丄CD 偲偺愙揰傪偦傟偧傟D丄E丄F 偲偡傞丅偙偺偲偒丄O1DA 偼捈妏嶰妏宍偱
佢O1AD = 30亱側偺偱丄DA = 併3r1偱偁傞丅
捈妏嶰妏宍偺嵍抂偺妏搙偑30亱偺偲偒偺斾棪偼侾懳俀懳併俁乮懳曈a亖侾丄幬曈b亖俀丄掙曈c亖併俁乯
2DA = DA + AE = CA - CD + AD - ED = CA - CF + AD - FD = CA + AD - CF - FD =
= a + b - d 傛傝丄 2併3r1 = a + b - d d = 2a - b - 2併3r 丒丒丒 幃嘇傛傝 2併3r1 = a + b - d
r1 = (a + b - 倓)乛2併3 = (- a + 2b + 2併3r)乛2併3 丒丒丒 幃嘋
仮ADC 偵懳偟偰丄揰D 偐傜曈AC 偵堷偄偨悅慄偺挿偝h (Sin 60亱= 併3/2 傛傝) 偼 h =併3b/2丒丒丒 幃嘍
h(r2 + r3 - r1) - 2r2r3 = 0
仮ADC 偵曗彆掕棟侾 傪梡偄傞偙偲偵傛傝丄 2hr - 2r^2 - hr1 = 0 丒丒丒 幃嘐 偱偁傞丅
偙偺曗彆掕棟1 偼榓嶼壠偑曇傒弌偟偨廳梫側岞幃偱丄偙偺岞幃傪梡偄傞偙偲偱屻偺寁嶼偑娙寜偵側傞
BD = a - b = (a(併3a - 4r) - (併3a^2 - 8ar + 4併3r^2))乛(併3a - 4r)
亪 BD = (4ar - 4併3r^2)乛(併3a - 4r) = 4r(併3r - a)乛(4r - 併3a)
幃嘋 偲幃嘍 傪 幃嘐偵戙擖偟惍棟偡傞偲丄r = (- a + 2b + 2併3r)乛2併3 h =併3b/2
(倎 - 倐 + 們)^2丂傪揥奐偡傞丅 (倎 - 倐) = A 偲偡傞丅 ( A + 們)^2 = A^2 + 2A們 + 們^2 =
(倎 - 倐)^2 +2(倎 - 倐)們 + 們^2 = a2 - 2ab + b2 + 2ac - 2bc + c^2 = a2 + b2 + c^2 - 2ab + 2ac - 2bc
2hr - 2r^2 - hr1 = 0 傛傝 丂 2(併3b/2)r - 2r^2 - (併3b/2)(- a + 2b + 2併3r)乛2併3 = 0
併3br - 2r^2 - (併3b)(- a + 2b + 2併3r)乛4併3 = 0 併3br - 2r^2 - b(- a + 2b + 2併3r)乛4 = 0
(ab - 2b^2 + 2併3br - 8r^2 )乛4 = 0 亪 ab - 2b^2 + 2併3br - 8r^2 = 0丂 丒丒丒 幃嘊傪戙擖偡傞丅
ab - 2b^2 + 2併3br - 8r^2 = 0 倐 = a - 4r(併3r - a)乛(4r - 併3a) 傛傝
a(a - 4r(併3r - a)乛(4r - 併3a)) - 2((a - (4r(併3r - a)乛(4r - 併3a))^2 + 2併3r(a - 4r(併3r - a)
乛(4r - 併3a))- 8r^2))
= (4a^2r - 併3a^3 - 4併3ar^2 + 4a^2r)乛(4r - 併3a) - 2(a^2 - (8併3ar^2 - 8a^2r)乛(4r - 併3a))
+ (48r^4 - 32併3ar^3 + 16a^2r^2)乛(4r - 併3a)^2 + (((- 6a^2r - 24r^3 + 16併3ar^2))乛(4r - 併3a))- 8r^2)
= ((- 24r^3 + 12併3ar^2 + 2a^2r - 併3a^3)(4r - 併3a)乛(4r - 併3a)^2 - 2((48r^4 - 64併3ar^3 + 88a^2r^2
- 16併3a^3r + 3a^4)乛(4r - 併3a)^2) = 8r^2
丂丂丂丂丂丂丂丂
= ((- 192r^4 + 200併3ar^3 - 204a^2r^2 + 26併3a^3r - 3a^4)乛(4r - 併3a)^2) = 8r^2
= (4r - 併3a)^2((- 192r^4 + 200併3ar^3 - 204a^2r^2 + 26併3a^3r - 3a^4)乛(4r - 併3a)^2) =
8r^2(4r - 併3a)^2)
= (- 192r^4 + 200併3ar^3 - 204a^2r^2 + 26併3a^3r - 3a^4 - 128r^4 + 64併3ar^3 - 24a^2r^2)
= (- 192r^4 - 128r^4 + 200併3ar^3 + 64併3ar^3 - 204a^2r^2 - 24a^2r^2 + 26併3a^3r - 3a^4)
- 320r^4 + 264併3ar^3 - 228a^2r^2 + 26併3a^3r - 3a^4 = 0
丂亪 3a^4 - 26併3a^3r + 228a^2r^2 - 264併3ar^3 + 320r^4 = 0
丂仸 r = 併3/6*ax丂偲偡傞丅 a = 20 (悺) 傛傝
3a^4 - 26併3a^3r + 228a^2r^2 - 264併3ar^3 + 320r^4 = 0
3a^4 - 26併3a^3(併3/6ax) + 228a^2(併3/6ax)^2 - 264併3a(併3/6ax)^3 + 320(併3/6ax)^4 = 0
3a^4 - 26a^3(1/2)*ax + 228a^2(1/12)*a^2x^2 - 264併3a(3併3/216)*a^3x^3 + 320(9/1296)*a^4x^4 = 0
3a^4 - 13a^4x + 19a^4x^2 - 264(1/24)*a^4x^3 + 320(1/144)*a^4x^4 = 0
3a^4 - 13a^4x + 19a^4x^2 - 11a^4x^3 + 20/9a^4x^4 = 0 丂 椉曈偵 9/a^4 傪妡偗偰惍棟偡傞丅
27 - 117x + 171x^2 - 99x^3+ 20x^4 = 0 丂 椉曈偵 9/a^4 傪妡偗偰惍棟偡傞丅
20x4 - 99x3 + 171x2 - 117x + 27 = 0 丒丒丒 偙偺
係師曽掱幃 傪夝偔
x = 0.513
r = 併3/6*20*0.513 = 2.96180688094
亂奜墌 傪媮傔傞亃
丂丂丂丂丂丂丂丂丂丂丂丂丂丂
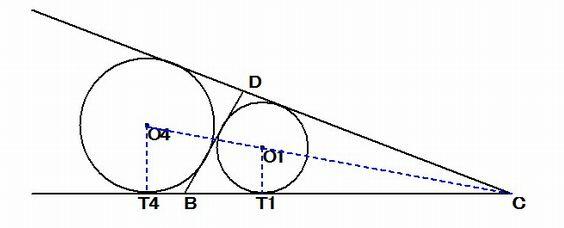
奜墌偺拞怱傪 O4 偲偟丄偦偺敿宎傪 倰4 偲偡傞丅捈慄 BC 偲俀墌 O1, O4 偲偺愙揰傪 T1 , T4 偲偡傞丅
嚈O4T4C 佷 O1T1C 偵傛傝丂丂O4T4 丗 O1T1 = T4C 丗 T1C 曗彆掕棟俀 傛傝丄T4T1 = BD 偱偁傞丅
倰4 * T1C = 倰 * T4C r = 併3/6*ax 1.44337567297
BD = 4r(併3r - a)乛(4r - 併3a) = 4併3/6*ax(併3*併3/6*ax - a)乛(2併3/3ax - 併3a) =
2併3/3*ax(1/2*ax - a)乛(2併3/3*ax - 併3a) = 2併3/3*a^2x(1/2*x - 1)乛(併3a(2/3*x - 1)) =
2併3/3*a^2x((1x - 2)乛2)乛(併3a((2x - 3)乛3)) = 2併3/3*a^2x((1x - 2)乛2) * (3乛(併3a(2x - 3)) =
(併3*a^2x(1x - 2))乛(併3a(2x - 3)) = (ax((2 - x))乛(3 - 2x) 亪 丂BD = (ax((2 - x))乛(3 - 2x)
BT1 傪傕偲傔傞丅 O1DA 偼捈妏嶰妏宍偱 佢O1BT1 = 30亱側偺偱丄BT1 = 併3r = 1/2*ax
r4 = 倰*T4C乛T1C = r(T1C + (T4T1乛T1C)) = r(1 + T4T1乛T1C) = r(1 + (BD乛(BC - BT1)) =
併3/6*ax(1 + ( (ax((2 - x))乛(3 - 2x)乛(BC - BT1)) =
併3/6*ax乷1 + ((ax(2 - x)乛(3 - 2x)))乛(a - 1/2*ax)乸 =
併3/6*ax乷1 + ((ax(2 - x))乛(3 - 2x)))乛(a(2 - x)乛2)乸= 併3/6*ax(1 + ((ax(2 - x))乛(3 - 2x))) * 2乛(a(2 - x))) =
併3/6*ax乷1 + ((2ax(2 - x)乛(a(3 - 2x)(2 - x))乸 = 併3/6*ax乷1 + (2x乛(3 - 2x))乸 =
併3/6*ax乷(3 - 2x + 2x)乛(3 - 2x))乸 = 併3/6*ax(3乛(3 - 2x) = 併3ax乛2(3 - 2x) =
(併3*20*0.513)乛(2(3 - 2*0.513)) = 4.50122626283
r4 = 併3ax乛2(3 - 2x) = 4.50122626283 偲側傝
奜墌偺捈宎偼丄 2r4 = 9.00245252566 偱偁傞丅丂丂丂
丂亪丂嶼妟偺摎濰丂奜殺宎嬨悺楇楇桳婏 ( 嬨悺僛儘僛儘梋傝桳傝乯
丂丂丂仭曗彆掕棟侾仭
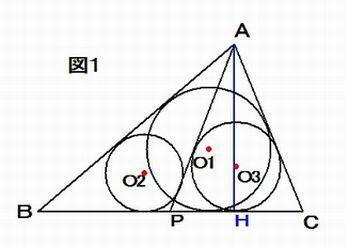
恾1 偺傛偆偵3 墌O1, O2, O3 偼偦傟偧傟ABC, ABP, APC 偺撪愙墌偲偡傞丅
傑偨丄捀揰A偐傜曈BC 偵壓傠偟偨悅慄偺懌傪H 偲偡傞丅 偙偺偲偒丄墌O1, O2, O3 偺敿宎傪偦傟偧傟r1, r2, r3 偲偟丄
AH = h偲偡傞偲偒丄 h(r2 + r3 - r1) - 2r2r3 = 0 丒丒丒 嘆 偱偁傞丅
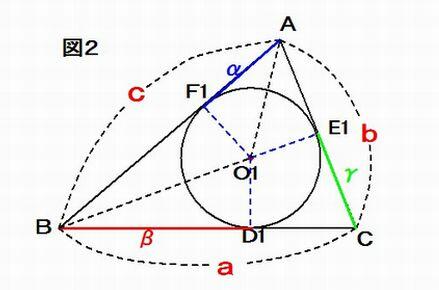
亂徹柧亃 恾2偺傛偆偵丄3 曈BC, CA, AB 偺挿偝傪偦傟偧傟a, b, c 偲偟丄
僿儘儞偺岞幃丂傛傝丂丂s = (a+b+c)/2 偲偡傞丅
傑偨丄撪愙墌O1 偑3 曈BC, CA, AB 偲愙偡傞揰傪偦傟偧傟D1, E1, F1偲偟丄AF1 = 兛, BD1 = 兝, CE1 = 兞 偲偡傞丅
恾2偺傛偆偵3曈偺挿偝偑a,b,c偺嶰妏宍ABC偵O1傪拞怱偲偡傞敿宎r1偺墌偑撪愙偟偰偄傑偡丅
偙偺帪丄O1偼撪怱偲屇偽傟丄 仮AF1O1佭(崌摨)仮AE1O1丄仮BF1O1佭仮BD1O1丄仮CD1O1佭仮CE1O1偲側傝傑偡丅
s = (a+b+c)/2 = 2 ((兛r1/2) + (兝r1/2) + (兞r1/2)) = 2 r1(兛 + 兝 + 兞)乛2 = r1(兛 + 兝 + 兞)
2s = a+b+c = 2(兛 + 兝 + 兞) 2兝= 2s - 2(兛 + 兞) 2兞= 2s - 2(兛 + 兝 )
亪 兝 = s - b, 兞 = s - a 丒丒丒 嘇 偱偁傞丅
師偵丄恾3 偺傛偆偵丄曈BC 偲2 墌O2, O3 偺愙揰傪偦傟偧傟D2, D3 偲偡傞丅
O1BD1 偲O2BD2 偼憡帡側偺偱丄BD1 丗 BD2 = 兝 丗 BD2 = r1 丗 r2丄摨條偵CD1 丗 CD3 = 兞 丗 CD3 = r1 丗 r3
偲側傞丅 r1BD2 =r2兝 r1CD3 =r3兞 廬偭偰丄 BD2 =r2(s - b)乛r1, CD3 =r3(s - c)乛r1 丒丒丒 嘊 :
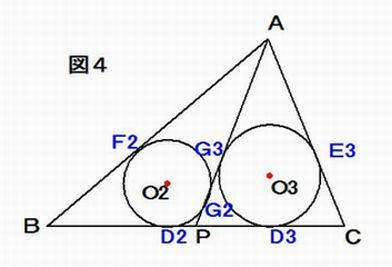
恾4 偺傛偆偵丄墌O2 偑AB, AP 偲愙偡傞揰傪偦傟偧傟F2, G2 偲偟丄墌O3 偑AC, AP 偲愙偡傞揰傪偦傟偧傟E3, G3 偲偡傞丅
偙偺偲偒丄仮ABP 偺柺愊偼丄 仮ABP = r2(AB + BP + PA)乛2 = r2(AB + BP + PG3 + AG3)乛2 =
r2(AB + BP + PD3 + AE3)乛2 = r2(AB + BD3 + AE3)乛2 = r2(AB + BC - .CD3 + CA - CE3) 乛2=
r2(a + b + c - 2CD3)乛2 = r2(s - CD3) 亪 仮ABP = r2(s - CD3)
偱偁傞丅 仮APD 偺柺愊偵偮偄偰傕摨條偱偁傞丅 仮APC = r3(s - BD2) 偲側傞丅
BD2 =r2(s - b)乛r1, CD3 =r3(s - c)乛r1
丂嘊 傪戙擖偡傞偲丄 仮ABP = r2s - r2r3(s - c)乛r1, 仮APC = r3s - r2r3(s - b)乛r1 偱偁傞丅
仮ABP + 仮APC = 仮ABC = 1ah/2 側偺偱丄 r2s - r2r3(s - c)乛r1 + r3s - r2r3(s - b)乛r1 =
(r2 + r3)s - r2r3(2s - b - c)乛r1= 1ah/2 丂s = (a+b+c)/2丂傛傝丂2s = a+b+c a = 2s - b - c
(r2 + r3)s - ar2r3/r1= 1ah/2 (r2 + r3)r1s - ar2r3 = (1ah/2)r1 (r2 + r3)r1s - ar2r3 - (1ah/2)r1 = 0
r1 s = 1ah/2 偱偁傞偙偲偵傛傝丄 岞幃 h(r2 + r3 - r1) - 2r2r3 = 0 偑摼傜傟傞丅
丂丂丂仭曗彆掕棟俀仭
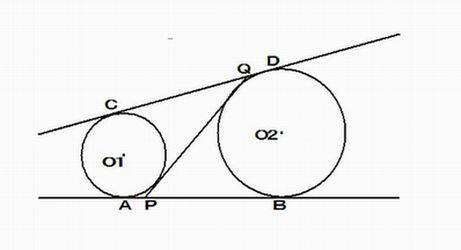
丂恾偺傛偆偵丄2 墌O1丄O2 偺嫟捠奜愙慄傪AB丄CD 偲偟丄嫟捠撪愙慄傪PQ 偲偡傞丅
偙偺偲偒丄AB = CD = PQ偱偁傞丅丂
丂愙慄偺惈幙傛傝丄AB = CD 偼柧傜偐偱偁傞丅
嫟捠撪愙慄PQ 偲2 墌O1, O2 偲偺愙揰傪偦傟偧傟E, F偲偟丄PA = PE = p丄QD = QF = q 偲抲偔丅
偙偙偱丄AB = p + PB = p + PF = 2p + EF 偲CD =CQ+ q = EQ + q = EF + 2q 偵傛傝丄AB = CD 偐傜p = q
偑摼傜傟丄岞幃AB = CD = PQ 傪摼傞丅


 +
+