■補助定理1■

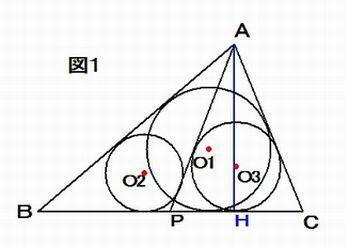
 図1 のように3 円O1, O2, O3 はそれぞれABC, ABP, APC の内接円とする。

また、頂点Aから辺BC に下ろした垂線の足をH とする。 このとき、円O1, O2, O3 の半径をそれぞれr1, r2, r3 とし、

AH = hとするとき、 h(r2 + r3 - r1) - 2r2r3 = 0 ・・・ 式�@          である。

                            

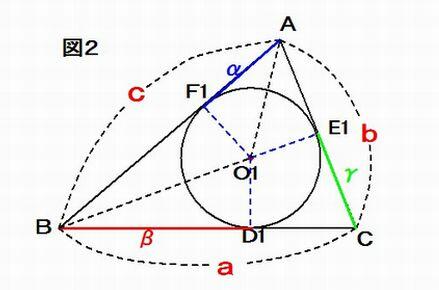
【証明】 図2のように、3 辺BC, CA, AB の長さをそれぞれa, b, c とし、ヘロンの公式　より　　s = (a+b+c)/2 とする。

また、内接円O1 が3 辺BC, CA, AB と接する点をそれぞれD1, E1, F1とし、AF1 = α, BD1 = β, CE1 = γ とする。

                                  

 図2のように3辺の長さがa,b,cの三角形ABCにO1を中心とする半径r1の円が内接しています。

この時、O1は内心と呼ばれ、 △AF1O1≡△AE1O1、△BF1O1≡△BD1O1、△CD1O1≡△CE1O1となります。 

 s = (a+b+c)/2 = 2 ((αr1/2) + (βr1/2) + (γr1/2)) = 2 r1(α + β + γ)／2 = r1(α + β + γ) 

  このとき、  β = s - b, γ = s - a ・・・ 式�A である。 

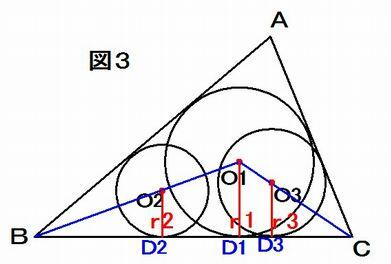
次に、図3 のように、辺BC と2 円O2, O3 の接点をそれぞれD2, D3 とする。

O1BD1 とO2BD2 は相似なので、BD1 ： BD2 = β ： BD2 = r1 ： r2、同様にCD1 ： CD3 = γ ： CD3 = r1 ： r3 

となる。 r1BD2 =r2β r1CD3 =r3γ 従って、 BD2 =r2(s - b)／r1, CD3 =r3(s - c)／r1 ・・・ 式�B  : 

                              

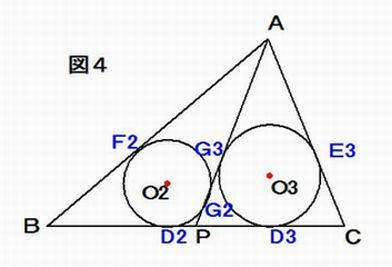
 図4 のように、円O2 がAB, AP と接する点をそれぞれF2, G2 とし、円O3 がAC, AP と接する点をそれぞれE3, G3 とする。このとき、△ABP の面積は、 △ABP = r2(AB + BP + PA)／2 = r2(AB + BP + PG3 + AG3)／2 =

r2(AB + BP + PD3 + AE3)／2 = r2(AB + BD3 + AE3)／2 = r2(AB + BC - .CD3 + CA - CE3) ／2= 

r2(a + b + c - 2CD3)／2 = r2(s - CD3) ∴  △ABP = r2(s - CD3)

である。 △APD の面積についても同様である。         △APC = r3(s - BD2)  となる。

 BD2 =r2(s - b)／r1, CD3 =r3(s - c)／r1

　式�B を代入すると、 △ABP = r2s - r2r3(s - c)／r1, △APC = r3s - r2r3(s - b)／r1  である。

 △ABP + △APC = △ABC = 1ah/2 なので、 r2s - r2r3(s - c)／r1 + r3s - r2r3(s - b)／r1 =

(r2 + r3)s - r2r3(2s - b - c)／r1= 1ah/2 　s = (a+b+c)/2　より　2s = a+b+c a = 2s - b - c

 (r2 + r3)s - ar2r3/r1= 1ah/2 (r2 + r3)r1s - ar2r3 = (1ah/2)r1 (r2 + r3)r1s - ar2r3 - (1ah/2)r1 = 0   

  r1 s = 1ah/2 であることにより、 公式   h(r2 + r3 - r1) - 2r2r3 = 0   が得られる。