Top page (correct Bohr model including helium. )
Strange "spin" is NOT a real thing
Singlet and Triplet don't mean "Spin".
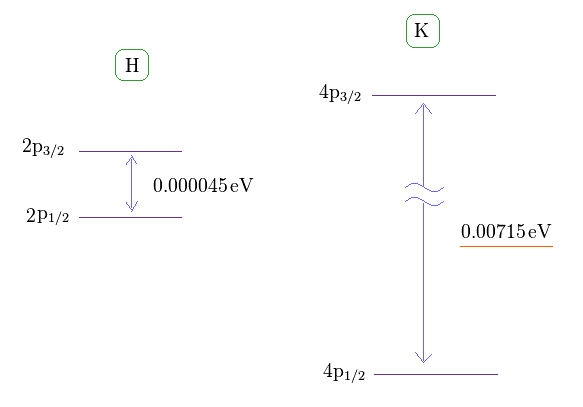
(Fig.1) Hydrogen and potassium fine structure (= D line ).
On this page, we show sodium D-lines energy splitting is too wide to explain by the weak relativistic spin-orbit interactions.
It is quite natural that we think these unrealistically large effects in D lines are due to some Coulomb interactions with inner electrons.
On this page, we show D-line or fine structure energy splittings in all other alkali metals such as potassium (= K ), rubidium (= Rb ), and cesium (= Cs ) are unrealistically too big for the tiny relativistic spin-orbit effect.
On this site, hydrogen fine structure (= doublet ) between 2p3/2 and 2p1/2 is about 0.000045 eV (= 0.4 T ).
The fine structure between 4p3/2 and 4p1/2 of potassium is as big as 0.00715 eV, as shown on this site (p.7, n.67) or nist where 4p3/2-4p1/2 = 57.7 cm-1 equals 0.00715 eV.
(Fig.2) Spin-orbit interaction ? → Central charge Z becomes "too big".
(Fig.3) Energy difference between p3/2 and p1/2
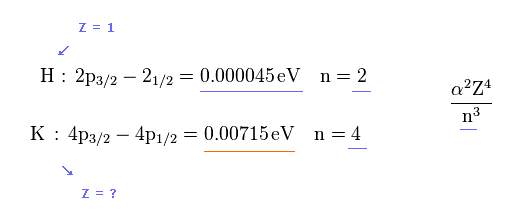
Relativistic spin-orbit magnetic energy splitting between two energy levels (= same principal number n, same orbital angular momentum l = 1 , different total angular momentum j = 1/2 and j = 3/2 ) is proportional to Z4/n3 where Z is the effective central charge containing nuclear charge and all inner electrons except one valence electron ( this p.9-(1.37), this p.9-(5.32), this p.3-left-1st-paragraph, this p.9-lower ).
In hydrogen atomic D-line or fine structure, Z = 1 and n = 2 (= energy splitting between 2p3/2 and 2p1/2).
In potassium atom, n =4.
From these values and experimental D-line energy splitting ( H atom-0.000045 eV vs. K-0.00715 eV, this p.5-Table 1 ), we can determine effective central charge Z of potassium.
(Fig.4) Z of potassium is too big (= 5.97 ).
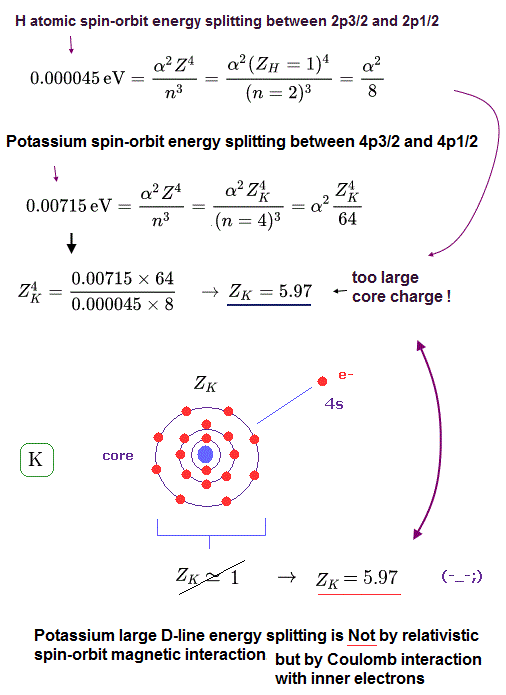
From Fig.3 and Fig.4, the effective core charge (= effective charge combining K nuclear + all inner electrons) of K becomes as large as Z = 5.97, which is unrealistic.
This core charge is the total charge summing up K nucleus and all 1n, 2n, 3n electrons.
The charge of K+ ion ( excluding only 4s electron ) is about +1e.
So, this core charge "Z" must be close to "1" also in K.
In conclusion, it is very impossible that the fine structure of potassium D lines is caused by spin-orbit interaction.
.
(Fig.5) Coulomb and large (core) orbit - orbit interactions generate "K" D lines.
Alkaline large D-line energy splitting is caused by Coulomb electric interaction between inner and outer electrons, Not by paradoxical tiny relativistic spin-orbit magnetic interaction.
(Fig.6) What is effective core charge Z from ionization energy ?
As shown in Fig.4, if spin-orbit interaction is real, effective core charge Z of potassium becomes much bigger (= 5.97 ) than "1".
We can know the real effective core charge Z from ionization energy of potassium ( 4s ) outer electron.
This ionization energy of potassium (= valence electron ) is 4.34 eV.
(Fig.7) hydrogen-like atoms
Fig.7 is energy levels expressed by "n (= principal quantum number )" and "Z (= central charge )" of hydrogen like atoms.
As you know, hydrogen ionization energy of 1s electron is 13.606 eV.
In 1s hydrogen, Z = 1 and n = 1.
(Fig.8) True effective core charge is Z = 2.259 in potassium.
Considering the principal quantum number ( n = 4 ), ionization energy (= 4.34 eV ) in "K" and Fig.7, we get the effective central charge Z = 2.259 in K 4s electron.
This true effective core charge (= 2.259 ) based on experimental ionization energy is much smaller than Z = 5.97 in Fig.4 assuming potassium large D-line splitting may be caused by tiny relativistic spin-orbit magnetic interaction.
As a result, the concept of (relativistic) spin-orbit coupling is too weak (= so need fictional large central charge Z = 5.97 ) to explain large D-line energy splitting between 4p3/2 and 4p1/2 in potassium.
(Fig.9) Fine structure of Rb.
As shown on this site (p.5, Table 1), the D-line energy difference between 5p3/2 and 5p1/2 in Rb is 0.02946 eV.
This fine structure of Rb is much bigger than hydrogen (= 0.000045 eV ), too.
(Fig.10) Effective central charge Z = 10.25 is too large.
Like potassium case, we can compute effective central charge based on spin-orbit and ionization energies.
Central charge based on the spin-orbit energy splitting equation becomes too large ( Z = 10.05 ) in comparison to true effective charge ( Z = 2.77 ) based on experimental ionization energy (= 4.177 eV ).
This result shows spin-orbit interaction of Rubidium is wrong, too.
(Fig.11) Fine structure of Cs.
As shown on this site (= p.5, Table 1 ), the energy difference between 6p3/2 and 6p1/2 in Cs is 0.06869 eV (or 0.06875eV ).
This fine structure of Cs is much bigger than hydrogen (= 0.000045 eV ), too.
(Fig.12) Effective central charge Z = 14.248 is too large.
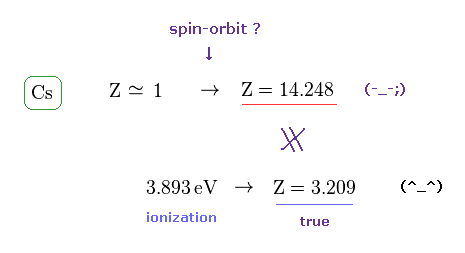
Like potassium case, we can compute effective central charge based on spin-orbit and ionization energies.
Central charge assuming the tiny relativistic spin-orbit interaction may cause D-line energy splitting becomes too large ( Z = 14.248 ) in comparison to true effective charge ( Z = 3.209 ) based on experimental ionization energy (= 3.893 eV ).
This result shows spin-orbit interaction of cesium needing the unrealistically-large central charge Z =14.248 is wrong, too.
(M.1) Quantum mechanics cannot predict electron spin. Even empirical ad-hoc Hund rule failed to explain experimental results.
Electron spin is unreal, Not true spinning, and disagreeing with experimental results.
Quantum mechanics cannot predict any (fictional) electron spin's phenomena.
Physicists created artificial empirical Hund rule (= Not quantum mechanical prediction ) and Lande spin-orbit-g-factor to explain some 4f-orbital rare earth atomic magnetic moment (= but even these artificial rules still failed to explain some rare earth metals, so No evidence of quantum mechanical spin ).
These Hund and Lange-spin-orbit rules completely disagree with 3d-orbital transition metallic magnetic moments, so they suddenly change the rules (= making all orbital angular momentum L = 0, which is unreal, and the original Lande-g-factor based on spin-orbit coupling is invalid ).
All these quantum mechanics, empirical Hund, Lande spin-g-factor theory are unable to explain other atoms such as 4d, 5d-orbital metallic magnetic moments ( this p.1-intro, this p.10-left-2nd-paragraph ).
Magnetic moments of ordinary ferromagnets such as Fe, Ni, Co also cannot be explained by quantum mechanical spin Lande g-factor, Hund rule ( this p.31, this p.34-last-paragraph ).
There are many other cases where Hund rule and artificial selection rule, Lande g-factor, Russell-Saunders spin-orbit (= LS )-coupling are violated ( this p.4-last, this-p.35,p.39--warning, this p.21 ).
The orders of the triplet energy levels (= J = 0, 1, 2 ) of 1s2p of helium (= J = 2,1,0 ). Li+ (= J = 1,2,0 ) and 2s2p of beryllium (= J = 0,1,2 ) are completely different with No consistent quantum mechanical spin rule, which also violates Hund rule ( this-p.15-6th-paragraph ).
The lack of consistent quantum mechanical rules about (unphysical) electron spin means there is No experimental nor theoretical evidence of electron spin.
(M.2) Lande g-factor (= gJ ) × total angular momentum number J = magnetic moment ?
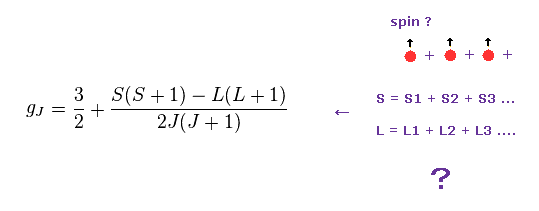
Quantum mechanical Lande g-factor was introduced to explain anomalous Zeeman effect of sodium fine structure energy splitting under applied magnetic field by using (unphysical) electron spin.
Lande g-factor (= gJ ) × total angular momentum m
↑ But this simple relation (= magnetic energy is linearly proportional to applied magnetic field B or Lande g-factor ) can Not be observed in actual experiments ( this p.38-39 ), so No evidence of Lande g-factor or electron spin.
In actual measurement of Alkali atomic magnetic moments in anomalous Zeeman effect and Lande g-factor, physicists have to artificially choose other free parameters such as A and B related to nuclear spin hyperfine energy (= total nuclear+spin-orbit angular momentum F = J + nuclear angular momentum I must be used instead of the original Lande g-factor, this p.3-5,p.25-26, this p.4, this p.3-5,p.7,p.28-39 ).
↑ Dependence on artificial irrelevant nuclear magnetic moment's free parameters (= A, B, gF ) in measurement of anomalous magnetic moment means there is No experimental evidence of quantum mechanical spin based on Lande g factor (= gJ ).
In atoms with multiple valence electrons, they have to artificially choose different rules of summing the total orbital and spin angular momentums based on LS (= Russell Sanders ) coupling, jj coupling or intermediate coupling (= choice of these different coupling patterns in different atoms is like choosing free parameters with No quantum mechanical prediction, this p.18, this p.7 ), which also cannot validate Lande g-factor or quantum mechanical spin.
(M.3) Only when applied magnetic field H or B is almost zero, the material's effective magnetic moment can be measured ?
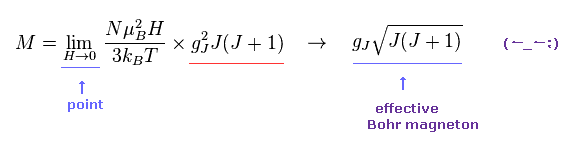
Curie-Weiss law is often used to indirectly estimate the material's effective magnetic moment under applied magnetic field H as a function of temperature T.
In this complicated Curie-Weiss law, only when the applied magnetic field H or B is extremely small ( H → 0 ), the material's magnetic moment is said to be obtained ( this p.2-7, this p.3.p.13 ). ← So this magnetic moment by this method is Not a universal value in any magnetic field.
↑ Physicists have to artificially choose temperatures and magnetic field (= like freely-chosen parameters ), and add ad-hoc parameters in some atoms to explain magnetic moments ( this p.6-left,p.6-right-2nd-last-paragraph ), which is Not a quantum mechanical prediction of spin.
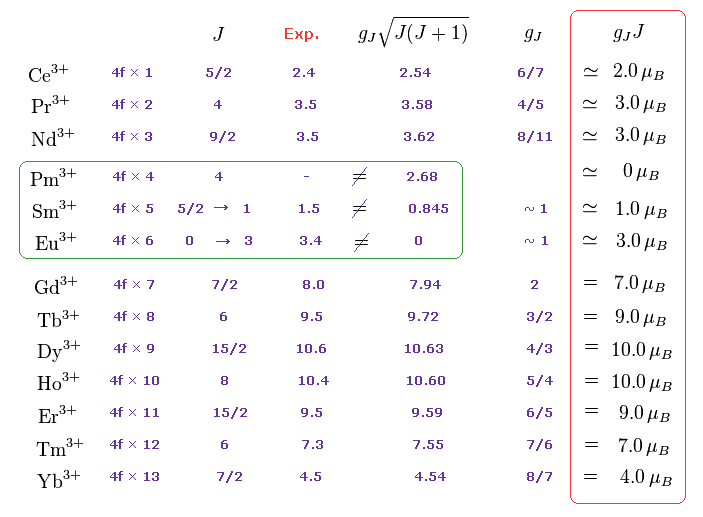
(M.4) Pm3+, Sm3+, Eu3+ completely disagree with magnetic moments of Hund rule (and quantum mechanical spin).
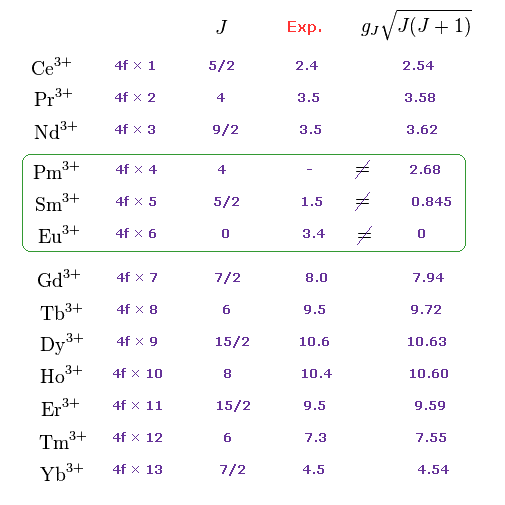
Empirical Hund rule combined with quantum mechanical Lande g factor, LS coupling rule and classical Curie law was artificially created to explain only magnetic moments of 4f-orbital rare earth atoms.
Even by applying artificially-modified Hund rule, the quantum mechanics failed to explain magnetic moments of rare earth such as Pm3+, Sm3+, Eu3+ ( this p.11 ).
J is the total angular momentum, L is orbital and S is spin angular momentum ( J = L ± S, this p.27 ).
(M.5) Hund rule, quantum mechanical Lande g factor (= gJ ) completely failed to explain experimental magnetic moments of metals, so they suddenly changed the rules and started to say all the metallic orbital angular momentums L appear to be zero, which clearly contradicts the fact.
Empirical Hund rule, quantum mechanical Lande g factor (= gJ ) was artificially created to explain (effective) magnetic moments of 4f rare earth atoms, though this attempt failed.
These artificial quantum mechanical rules using Lande g-factor gJ and J completely disagree with experimental magnetic moments of 3d transition metals, as shown in Fig.M5 ( this p.12-lower-p.13, this p.13-last-table ).
So they suddenly changed the rules, and started to say the orbital angular momentums L of all the 3d metals appear to be zero (= which disagree with the fact, this-middle~lower ), and only the values of spin S should be used (= Lande g-factor gJ mixing orbital L and spin S is ditched in 3d-metals ).
↑ In spite of this artificial change of rules just to explain the contradictory 3d metals, they failed to explain magnetic moments of Fe2+, Co2+, Ni2+.. after all ( this p.31, this p.34-last-paragraph, this p.15-1st-paragraph ).
All other 4d, 5d.. atoms disagree with these artificial Hund and quantum mechanical rule ( this p.1-intro ).
This p.10-left-2nd-paragraph says
"in the 4d and 5d
block. These materials tend to exist in a realm that is intermediate (= disobey the above quantum mechanical rule of 4f and 3d metals )
to the quenched orbital angular momentum of 3d transition
metals and the Hund’s rules adherence of 4f rare earth ions"
As a result, the quantum mechanical artificial ad-hoc spin rules such as Hund rule, LS-coupling and Lande f-factor failed to explain experimental magnetic moments, so quantum mechanics and its unphysical electron spin with No experimental nor theoretical evidence are unreal.
(M.6) To explain magnetic moment of the rare earth Pr3+, the total angular momentum J should be L minus S ? Because orbital (= L ) and spin (= S ) angular momentums are in the opposite direction ? ↓
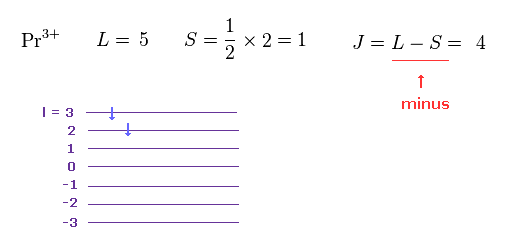
In order to apply the unphysical quantum mechanical spin to magnetic moments of rare earths, the empirical Hund rule was created.
The problem is this artificial Hund rule is based on inconsistent, contradictory rules, so unreal.
In M.6, this Hund rule says the total angular momentum J of the rare earth Pr3+ must be equal to orbital angular momentum (= L ) minus the spin angular momentum (= S, this p.9 ), which disagrees with other rare earths.
(M.7) In rare earth Dy3+, the sign of orbital (= L ) and spin (= S ) angular momentums are opposite, but the total angular momentum J = L + S instead of L - S ? ← inconsistent.
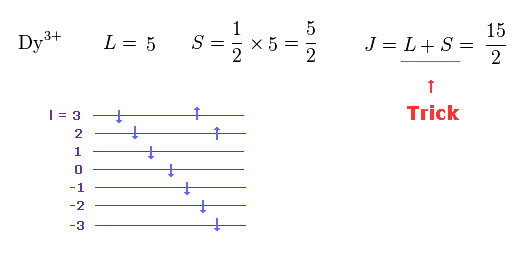
Also in the rare earth Dy3+, the signs of the orbital (= L = 2+3 = +5 ) and spin (= S = -1/2 × 5 = -5/2 ) are opposite like Pr3+ case.
But the ad-hoc Hund's rule says in this Dy3+ case, the total angular momentum J should be L + S (= J = 15/2, this p.2 ), which is clearly inconsistent and unreal.
(M.8) In cases of rare earths Eu3+, Gd3+, Tb3+
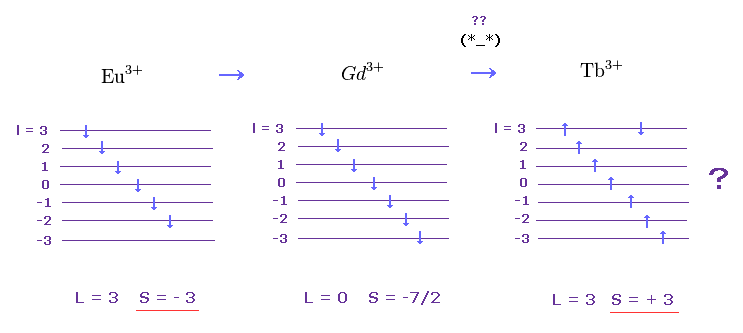
Feel free to link to this site.
