トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは単なる幻想にすぎない。
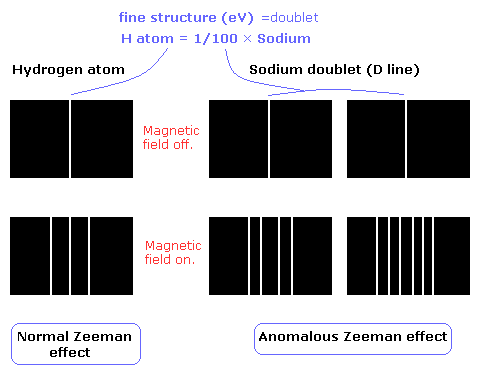
水素原子の ゼーマン効果 は、均等に3つに分かれる。(= "正常"ゼーマン効果)。
一方で、ナトリウムのD線 (D1, D2 dublet) は、"異常"ゼーマン効果を示す。 (これは たくさんある 内殻の電子によって生じると考えたほうが自然である。)
( Fig. 1 )

水素原子の 微細構造 (fine structure) はとても小さい (約 0.00005 eV)。これは ナトリウムの約 1/100 くらいしかない。
そのため、通常の磁場 (1T) のもとで 水素原子において ランデのg因子 (=異常ゼーマン効果) を確認することは不可能である。
もちろん、ボーア。ゾンマーフェルト模型は 電子スピンがないにも関わらず 微細構造について説明することができる。(このページも参照のこと。)
だから、ボーア模型を用いても いわゆる 偶数に (=doublet) 分離したスペクトル線は説明可能である。
正常ゼーマン効果は スピンがゼロ の状態で観察されるとされている。
しかし、はっきり言って 量子力学において 電子スピンの影響を無視することは不可能である (微細構造のことではなく)。
なぜなら、電子スピンといえども ħ の角運動量の軌道と同じ大きさの 磁気モーメント (= ボーア磁子) を持つからである。
(結果として、水素原子の基底状態の電子は ボーア模型と量子力学的模型で 同じ 磁気モーメント (= ボーア磁子) を持つことになる。)
つまり、Fig.1 の水素原子における 正常ゼーマン効果は 厳密には "パッシェンーバック効果" (Paschen-Back effect) をあらわしていることになる (Fig.2, 3)。
パッシェン・バック効果では、外磁場が 微細構造レベル (= スピン・軌道相互作用レベル) よりも強いとき、軌道とスピンの角運動量が 外磁場 (B) の方向に量子化される (Fig.2 参照)。
スピンg因子 (=2) は 軌道のg因子 (=1) の2倍であるため、磁場 (B) のもとでのエネルギー準位の差は その両方において "ボーア磁子 (Bohr magneton) × B" となる ( 2 × 1/2 = 1 × 1 より)。
( Fig. 2 ) 水素原子における パッシェン・バック効果=正常ゼーマン効果。
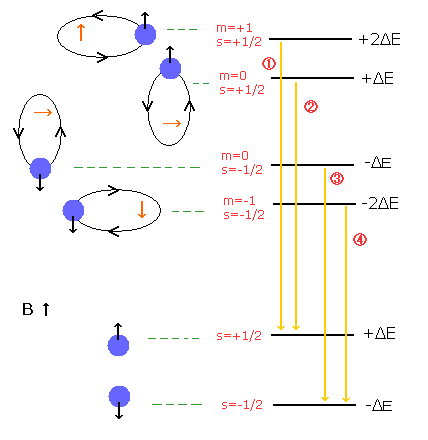
( Fig. 3 ) パッシェン・バック効果でも等間隔の3本線を示す。
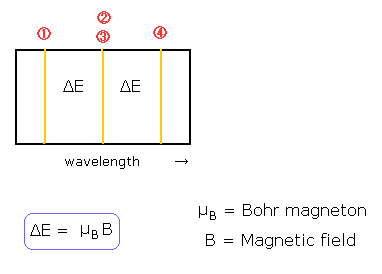
Fig.2 における 軌道角運動量の量子化は 不自然だと言わざるを得ない。
基本的に、外磁場のもとでは、磁気モーメントの N極はS極、S極はN極に引き寄せられる。
また、ローレンツ力によれば、軌道角運動量の方向は磁場の方向に平行になる。
(注意:これら2つの効果は逆である。なぜなら ローレンツ力は 外磁場を打ち消す方向に双極子を形成するよう働くからである。)
つまり、外磁場は 電子の磁気モーメントの双極子を 磁場に平行にするような力を与える。
結果、電子の軌道面は "自然に" 外磁場に対して 垂直になるのが当たり前である。
しかし、Fig.2 の m = 0 の状態は、電子の軌道運動によって生じる磁気モーメントが 外磁場に対して垂直になっているのである。
これは とても不安定で 非常に不自然と言わざるを得ない。
一方で、ボーア・ゾンマーフェルト模型は "不自然な" m = 0 の 角運動量を用いることなく、3本の均等に分かれたスペクトル線 (= 正常ゼーマン効果) を説明することが可能である。
( Fig. 4 ) ボーア・ゾンマーフェルト模型における パッシェン・バック効果。
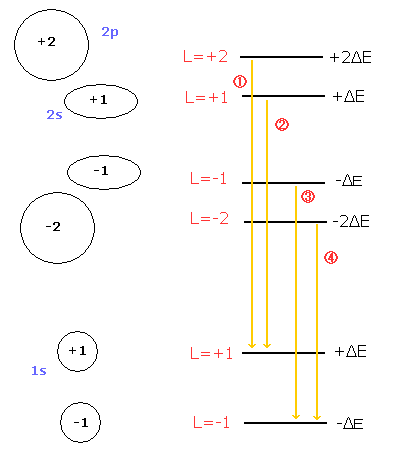
もし、2s と 2p の相対論的な質量変化 (=微細構造) の影響を無視できないほどの とても小さな 外磁場が加えられたとき、ボーア・ゾンマーフェルト模型においても 偶数に分離したスペクトル線を説明可能である。
1s の状態の電子は 2s の電子よりも当然 スピードが速いため、磁場によるローレンツ力は 1s 状態で より強くなる。
(もちろん 相対論的効果も 1s は 2s よりも強いことは言うまでもない。)
Fig.4 の 1s における 2つの +1 と -1 の状態は 回転方向が逆のため、磁場によって片方は内側方向、もう片方は外側方向への力を受ける。
そのため、1s の +1 と -1 の状態の相対論的な質量変化は 異なったものになる。
結果として、Fig.4 の line 2 と 3 は分離して、”偶数の”分離線が観察されることとなる。
しかし、水素原子において、ナトリウムのように 異常ゼーマン効果を正確に確認することは不可能である。
なぜなら、水素原子における 微細構造のエネルギー準位差は ナトリウムの約 1/100 ほどであるため、Fig.1 のナトリウムのような たくさんの線を観察することはできない。
また Fig.4 のボーア・ゾンマーフェルト模型は "不自然な" m=0 の状態を含んでいない。
(これが ボーア模型においても ステルン・ゲルラッハの実験での2つに分離する結果を再現できる理由である。)
もちろん、非常に弱い磁場のもとでは、ボーア・ゾンマーフェルト模型においても 磁気モーメントが完全に外磁場の方向を向かず 歳差運動する可能性はあり得る。
しかし、量子力学的な模型では、たとえ 外磁場がとても強くでも、必ず "不自然な" m = 0 の状態を含まなければならないのである。
おかしいこと この上ない。

2011/2/11 updated This site is link free.