微細構造定数の真実

トップページ (２電子原子も含む正確な新ボーア模型)
シュレデインガー方程式は ボーア・ゾンマーフェルト模型の 一部。
微細構造＝スピン軌道相互作用は 間違い。(14/8/17)

目次

• ボーア・ゾンマーフェルト理論は ”自然に”微細構造定数をだせる。
• ”相対論的な” ボーア・ゾンマーフェルト模型の計算。
• トーマス歳差因子とパウリの御裁可。
• ペニング・トラップによる異常磁気能率の測定。

ボーア・ゾンマーフェルト理論は ”自然に”微細構造定数をだせる。

ボーア・ゾンマーフェルト模型では、軌道の長さが ド・ブロイ波長の 整数倍 である。
驚くことに、そのシュレディンガー方程式においても 軌道の長さが ド・ブロイ波長の整数倍になるのである。
シュレディンガーの水素原子は このページ に示すように ドブロイ波長の名前を変える ことによって 非常に不合理な "不確定性原理" という概念を導入した。
これが シュレディンガー方程式が ボーア・ゾンマーフェルト模型と同じエネルギー準位を与える理由である。
このページで このことを”数学的に”証明した。

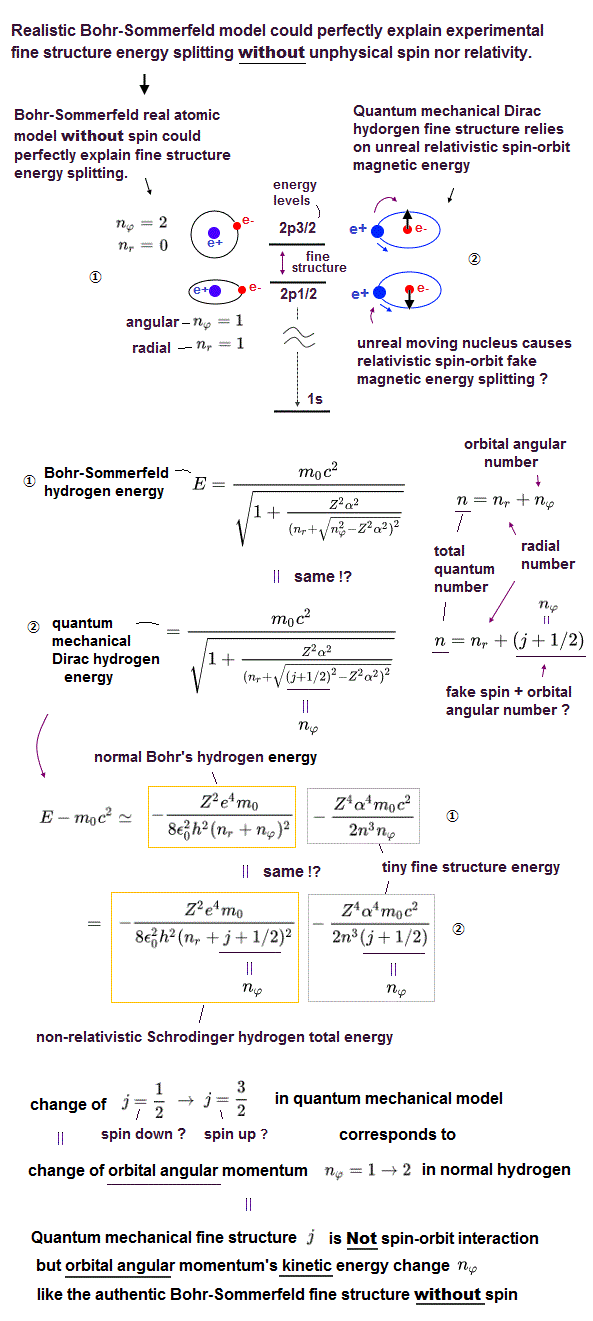
(Fig.1) ディラックの水素原子＝ボーア・ゾンマーフェルト模型。

多くの教科書では、水素原子の微細構造は 2p1/2 と 2p3/2 の間のエネルギーの違いを意味しており、これは 相対論的な ディラック方程式 によって導出できると書いてある。
驚くべきことに、このページ に示したように、このディラック方程式の解は何と ”相対論的な”ボーア・ゾンマーフェルト模型の解と完全一致している。
比較のために、この詳細な計算方法を知ることが必要である。
しかし、残念なことに 多くの教科書では ボーア・ゾンマーフェルト模型についてほとんど触れられていない。

２，３の教科書、例えば ディラック著 "The Principles of Quantum Mechanics (fourth edition)" の 272ページには、"this formula gives the discrete energy-levels of the hydrogen spectrum and first obtained by Sommerfeld working with Bohr's orbit theory." と、ディラック方程式による水素原子解の導出の後に、ゾンマーフェルトと同じ解であることを触れている。
また、朝永著 「スピンはめぐる」 には、ゾンマーフェルトの微細構造の解釈が スピン軌道相互作用に変えられた経緯を詳細に述べている。

ボーア・ゾンマーフェルト理論が 歴史的には 最初に 微細構造定数 (= 1/137.036..) をだしたのである。
このことは重要である。
ところで、ボーア・ゾンマーフェルト模型においては 微細構造定数の ”物理的な”意味 はいったい何なのだろうか？
このセクションでは 実際に 相対論的なボーア・ゾンマーフェルト模型を解いてみて、微細構造定数の 本来の意味とその導出について説明することにする。

(Fig.2) 実在のド・ブロイ波 (= "エーテル" )による ゾンマーフェルト模型。

実際は、”相対論的な”ゾンマーフェルト模型は 後で説明するが、”エーテル”理論を使って自然に表すことができる。"エーテル"による説明 も参照のこと。
正確には ボーア・ゾンマーフェルト模型は 特殊相対論そのものを 用いていない。
その 古典的極限を使用している。
もし "地球のエーテル" を認めれば、致命的な 直角レバーのパラドックス を生じさせずに 相対論的な質量変化を エーテル内の最高伝達速度で説明可能である。

[ 相対論的な場の量子論 ＝ 超光速のタキオン。 ]

ボーア・ゾンマーフェルト模型と 相対論的な場の量子論との 最も大きな違いは 超光速の "タキオン" の存在である。

( Fig.A-1 ) ボーア・ゾンマーフェルト模型。

ボーア・ゾンマーフェルト模型では、ドブロイ波は もちろん 光速よりも遅いスピード "v" で進んでいく ( v < c )。
ドブロイ波長 λ は h/p に等しい。 h はプランク定数、 p は 最高伝達速度を含めた運動量である。

( Fig.A-2 ) 相対論的な場の量子論。

クライン・ゴルドンやディラック方程式などの 相対論的な場の量子論は このページに示したように、アインシュタインのエネルギー・運動量の関係式に起因している。
もちろん、相対論的な場の量子論においても、ドブロイの関係式は使用されている。
問題は それらの波動関数の振動数が 質量エネルギーのため大きすぎるということである。
この非現実的に巨大な振動数が 超光速のタキオンを生じさせてしまう。

( Fig.A-3 ) 波動関数の振動数と運動量。

Fig.A-2 の式を満たす波動関数は Fig.A-3 になる。
ご存じのとおり、波の速度は 振動数 f ×；波長 λ ( v = fλ ) で与えられる。
そのため この波動関数の速度は
( Fig.A-4 )

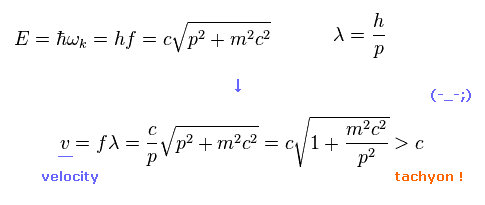
このスピードは 超光速である。
この理不尽な波動関数は 式のローレンツ変換不変性の要請から生じたものである。
皮肉にも 相対論的な制限が 想像上の粒子 "タキオン" を生じさせてしまったのである。

ディラック方程式で 正と負のエネルギー解を融合させれば、タキオンは消えると 彼らは主張しているが、電子と陽電子のそれぞれは 超光速であることに変わりはない。
( タキオン様の 仮想光子 も 相対論的なマクスウェル方程式から生じる。)

”相対論的な” ボーア・ゾンマーフェルト模型の計算。

( ボーア・ゾンマーフェルト模型。 )

以下の説明は ゾンマーフェルトの論文 ( Annalen der Physik [4] 51, 1-167, A. 1916 ) を基にしたものである。
特殊相対論に関しては、このページ も参照のこと。

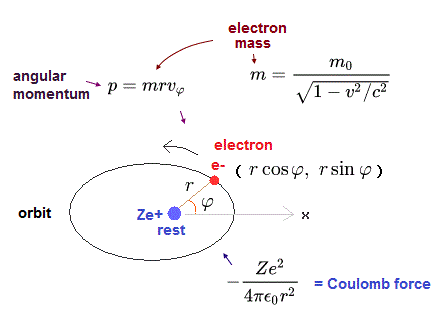
中心力をベースとした水素様原子においては、角運動量は一定である。
そのため、角運動量 (= "p" ) は次のようにあらわせる。
(Eq.1)

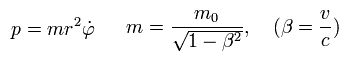
ここでは m₀ は 電子の 静止質量 で、 m は 相対論的な質量 である。
もし 速度 (= v) が 光速 (=c) に等しいとき、この相対論的な質量は 無限大になる。
このページに示したように、相対論的な質量は "直角レバーのパラドックス" を引き起こしてしまう。
つまり 相対論的質量は エーテルにおける最高伝達速度に起因すると考えるのが自然である。

次のように直交座標を極座標に変換する。
(Eq.2)

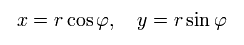
原子核が原点にあるとき、電子の運動方程式は クーロン力により 次のようになる。
(Eq.3)

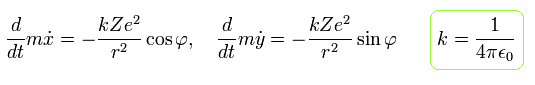
ここで Z は原子番号である。
ここではまた次のように定義してある。
(Eq.4)

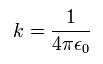
座標 r は φ の関数である。そのため t (= 時間) による微分を次のように表すことができる。（Eq.1 を使って。）
(Eq.5)

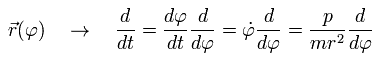
ここでは 次のように定義する。
(Eq.6)

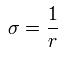
Eq.2 と Eq.5 を使って、各運動量は次のように表せる。
(Eq.7)

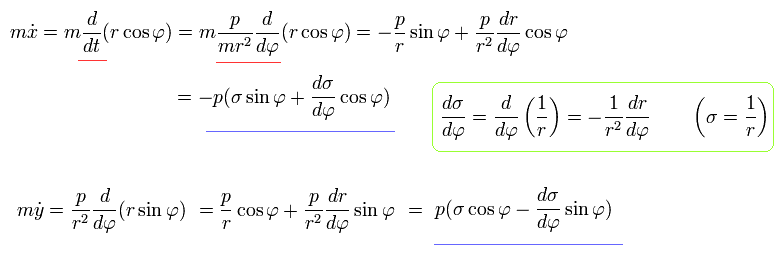
また、Eq.3, Eq.5, Eq.7 を使って、運動方程式は次のようになる。
(Eq.8)

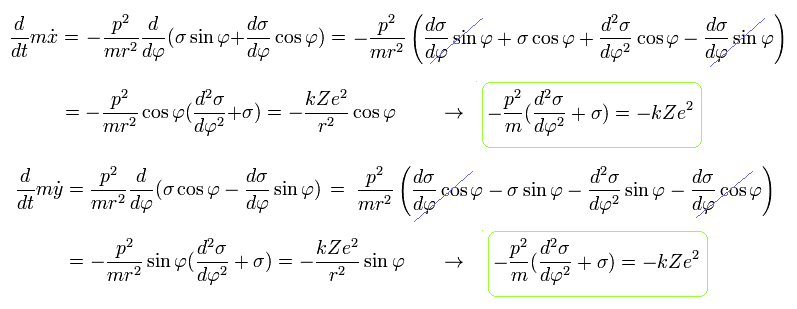
Eq.8 より、次のような 共通の 結果が得られる。
(Eq.10)

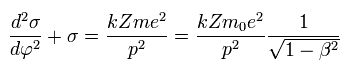
この β は 時間とともに変化しているため この β は別のものに置きかえる必要がある。

水素様原子では、ボーア・ゾンマーフェルト模型の 全エネルギー W (= T+V = 相対論的エネルギー (E) - m₀c²) は 次のようになる。
(Eq.11)

ここでは W は 運動エネルギーと位置エネルギーの和であり これは定数である。

正確に言えば、このページに示したように Eq.11 は 相対論的なエネルギーを表していない。
いわゆる 古典的極限の一種である。
また このページに示したように、相対論の E と p の２乗形は 奇妙な "仮想光子" を生じてしまう。
Eq.11 の W は それとは異なり、特殊相対論とは本質的に等価ではない。

Eq.11 からは Eq.6 の置き換えにより 次の式が得られる。
(Eq.12)

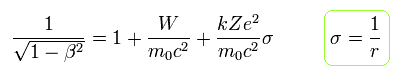
Eq.10 と Eq.12 から、
(Eq.13)

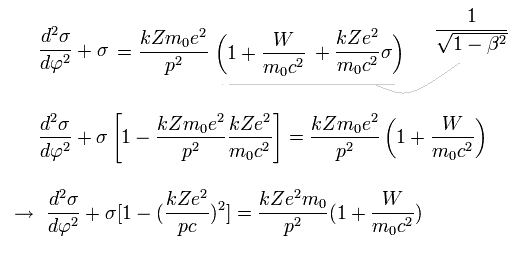
Eq.13 の σ の解は 次のように表せる。
(Eq.14)

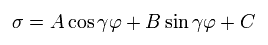
Eq.14 を Eq.13 に代入すると、 γ と C は 次のようになる。
(Eq.15)

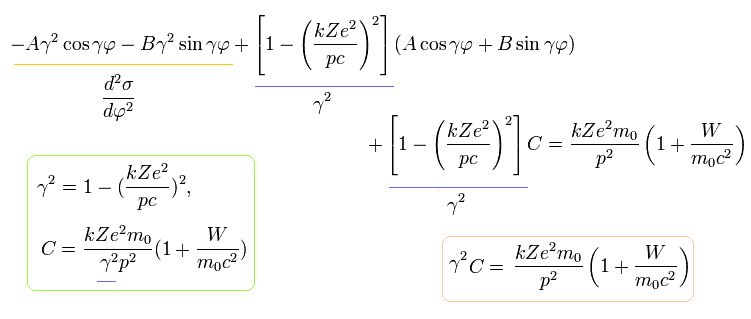
Eq.14 は r (= 1/σ) は 2π/γ ( 2π でなく) の角度 進むと 元に戻ることを示している。
そのため、”相対論的な”ボーア・ゾンマーフェルト模型の水素原子の軌道は、少し”歳差運動”していることになる。
例えば、１回転後、軌道の 近位点 は 次の角度進む。
(Eq.16)

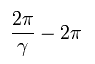
ここで 近位点の最初の位置を φ = 0 とする。
すると、 Eq.14 の B は 次のように ゼロになる。
(Eq.17)

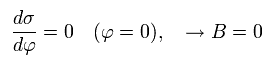
Fig.3 水素様原子の ”楕円形”の軌道。

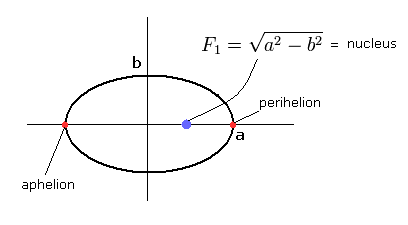
ここでは 原子核が焦点 (F₁) に位置しており、離心率 (=ε) は次のように表せる。
(Eq.18)

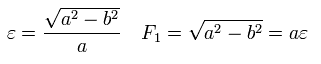
Eq.14 (B=0) と Eq.18 から、また Fig.3 の 近位点、遠位点を使って 次の関係式をだす。
(Eq.19)

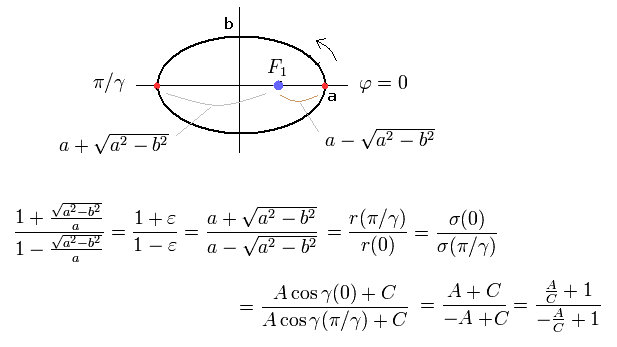
Eq.19, Eq.17 から Eq.14 における σ の A と B は 次のようになる。
(Eq.20)

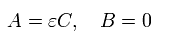
そのため r と σ は次のようにあらわせる。
(Eq.21)

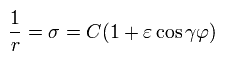
ここから、水素原子 (Z=1) を扱うことにする。
Z=1 を Eq.15 に代入して、次のように定義する。
(Eq.22)

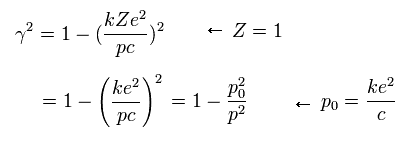
Eq.22 によれば、電子の角運動量 (p) が p₀ のとき、γ は ゼロ になる。
このことは p = p₀ のとき、Eq.16 の 歳差運動の速度 が 無限大 になることを意味する。
つまり ボーア・ゾンマーフェルトの水素原子では p₀ は 角運動量の下限極限 ということになる。
(もちろん、この場合では "楕円"軌道は 壊れてしまう。)

p₀ の ħ に対する比 ( = p₀/ħ ) が いわゆる "有名な" 微細構造定数 α である。
(Eq.23)

ここでは ħ ( = h/2π ) は ボーア模型における "量子化された" 最小の角運動量である。

つまり、微細構造定数 α (= 1/137) は ボーア・ゾンマーフェルト模型においては ”相対論的な”電子軌道における 歳差運動の速度 に関係しているのである。

------------------------------------
実は、この微細構造定数 α (= 1/137) は別のシンプルな方法でもだすことができる。（ このページも参照のこと。 )
普通のボーア模型の水素原子の満たす式を解く。（遠心力とクーロン力が等しく、また軌道長がド・ブロイ波長の１倍 (n=1)のとき。）
すると、この n=1 のボーア軌道の電子の速度 (v) は 次のようになる。

ボーア模型の水素原子における n=1 軌道の 電子の速度 (=v)。

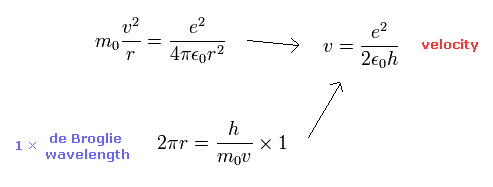
この電子の速度の 光速 (c) に対する比が 微細構造定数 α になる。

( 別の方法による微細構造定数の導出 = Eq.23. )

----------------------------------

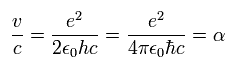
Eq.21 より、φ がゼロのとき、 σ、v、β は次のようになる。
(Eq.24)

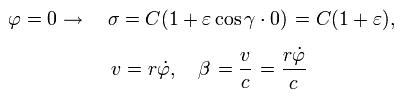
近日点では 速度は 接線方向である。

つまり、φ = 0 のとき、Eq.1, Eq.24, Eq.15 (Z=1) を使って 次の関係式が得られる。
(Eq.25)

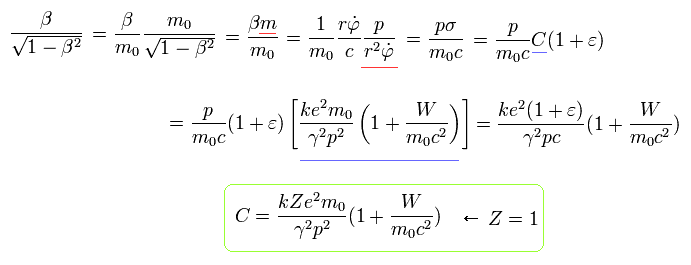
同様に、Eq.12, Eq.24, Eq.15 (Z=1) から、次の式が得られる。
(Eq.26)

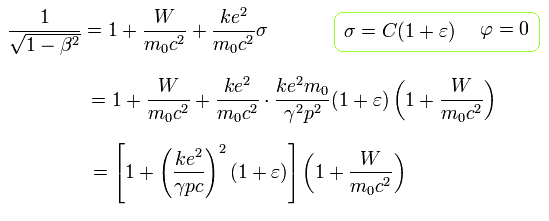
Eq.22 から、次の関係式を得る。
(Eq.27)

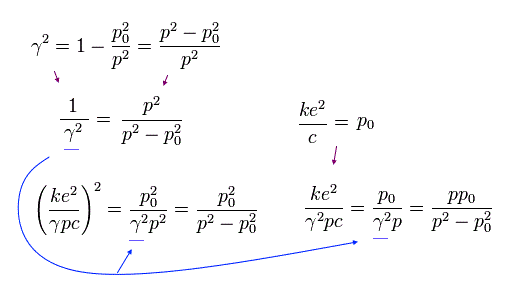
Eq.25, Eq.26, Eq.27 より、次のように β を消す。
(Eq.28)

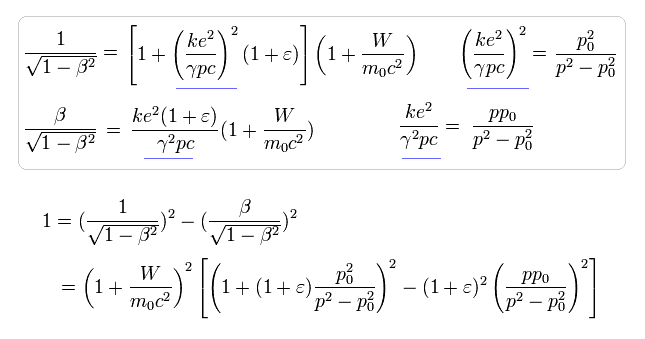
Eq.28 は 次に等しい。
(Eq.29)

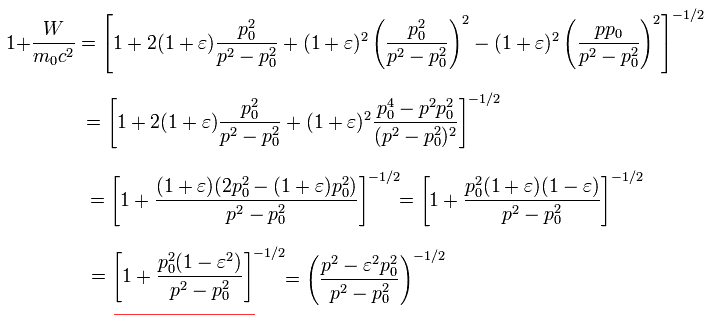
ボーア・ゾンマーフェルトの量子化条件では 次の関係式を用いる。
(Eq.32)

ここでは 角運動量 p は定数である。
そのため、 p は ħ の整数倍になる。

Eq.1 を用ると、 動径方向の運動量 p_r は次のように表せる。
(Eq.33)

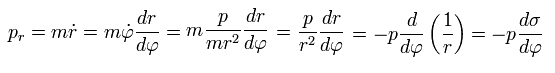
Eq.33、Eq.21 を用いて、Eq.32 の p_r を 次のように積分する。
(Eq.34)

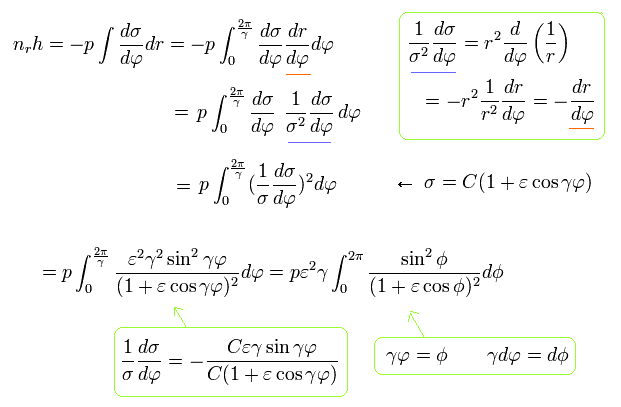
ここで 元の積分範囲は 歳差運動のため、0 から 2π/γ になる。
Eq.34 の最後の項では 次の置き換えを用いている。
(Eq.35)

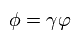
このページの Eq.39 - Eq.48 に示したように、部分積分と 次の複素積分を使用する。
(Eq.39')

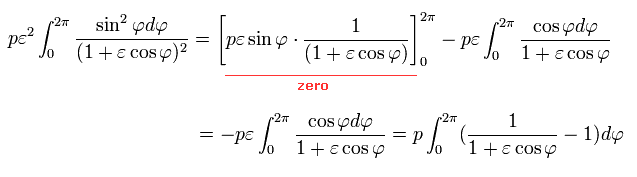
次の公式（複素積分）を用いる。
(Eq.40')

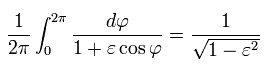
よって Eq.34 の結果は、Eq.22 の γ の置き換えを使って、
(Eq.36)

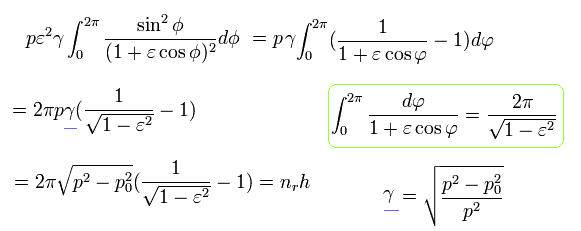
Eq.32 と Eq.22 を用いて、
(Eq.37)

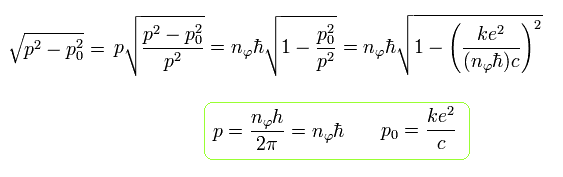
Eq.36 は Eq.37 を用いて、次の式に変わる。
(Eq.38)

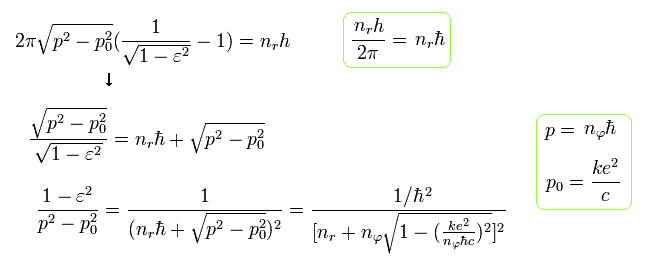
Eq.38 を Eq.29 の 赤線の項に代入して、Eq.23 の微細構造定数 α を用いると、
(Eq.39)

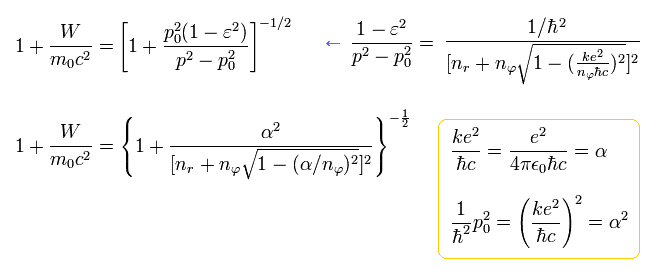
Eq.39 より、相対論的エネルギー ( E = W + m₀c² ) は、Z を付加して、
(Eq.40)

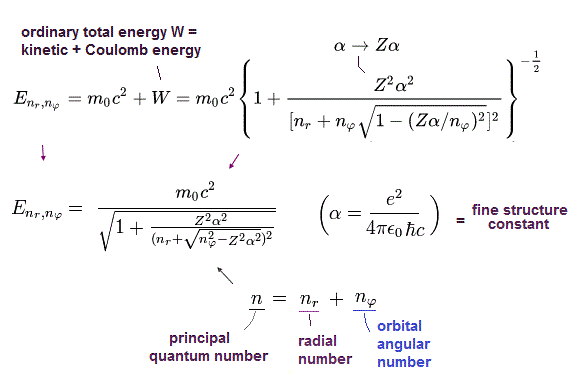
Eq.40 の ボーア・ゾンマーフェルトの解は Eq.41 の ディラック と 同じになる。
ディラック方程式の 計算の詳細については このページを参照のこと。
(Eq.41)

これはつまり Eq.41 のエネルギー準位は 次のように Eq.40 のと まったく等しくなる。

2p1/2 (n=2, j=1/2) -------- 2s (n_r=1, n_φ=1)
2p3/2 (n=2, j=3/2) -------- 2p (n_r=0, n_φ=2)

これは 驚くべき 偶然の一致である。

-------------------------------------------------------------------------------

[ "エーテル" を使った ボーア・ゾンマーフェルト模型。 ]

これらの事実に基づくと、 Fig.2 の式を 粒子の運動量として使用できる。
この場合は、微小時間 dt の間に 粒子を加速させるのに必要なエネルギー (= dT ) は、
(Eq.42)

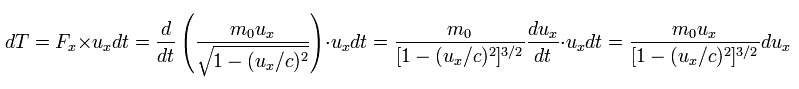
ここで u_x は x 方向の速度、 F_x は 力である。

ここで 次を使った。
(Eq.43)

つまり、粒子を 速度 v まで加速するのに必要な 全運動エネルギーは、
(Eq.44)

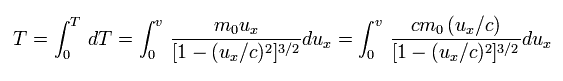
ここで 次の置き換えを使う。
(Eq.45)

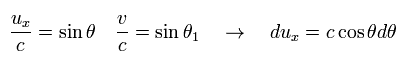
Eq.44 は、
(Eq.46)

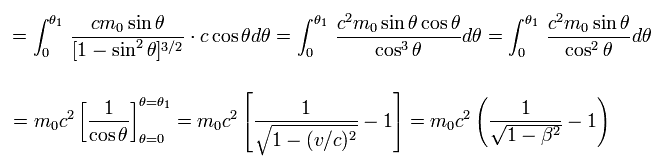
この運動エネルギーは 完全に Eq.11 の最初の項に等しい。

ボーア・ゾンマーフェルト模型は １次のエネルギー項を使用しており、もとの相対論 (= ２次の項もしくは ディラックのガンマ行列 ) とは異なる。
また もちろん、この模型は "時間の遅れ" のような奇妙な概念は使用していない。

この理論では、電子のスピード v が c に近づくにつれて 加速しにくくなる 運動量 (= p ) として 次を用いている。
( なぜなら ある媒質 (= エーテル) において その最高伝達速度が存在すると考えるのが自然だからである。 )
(Eq.47)

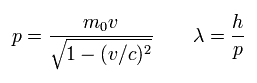
ここで λ は ドブロイ波長である。

Eq.42 と Eq..43 に示すように、 電場が 電子の進行方向 (= u_x ) へ 電子を加速するのに 必要な力 F_x は、
(Eq.48)

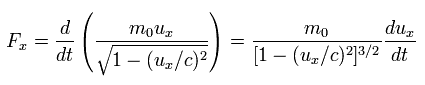
電場が この電子 ( u_y = 0 ) を y 方向へ加速するのに必要な力 F_y は、
(Eq.49)

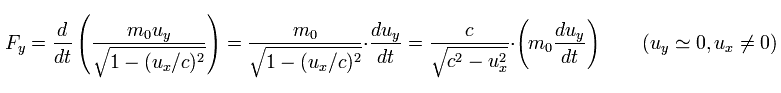
Eq.48 と Eq.49 に示すように、電場が 電子を 移動方向 (= x ) へ加速させるほうが y 方向へ加速させるよりも 力が必要である。
なぜなら 速度 u_x がゼロでないため x 方向へ 場が凝集しているため 抵抗が強くなるからである。
( この場合では 速度 u_y はゼロであるため、y 方向へは 場は凝集していない。)

つまり Eq.49 のほうが 場の凝集の効果を考える必要がなく 状況をイメージしやすい。

(Fig.4) 電子は x 方向へ動いている。 この電子を y 方向へ加速させる。

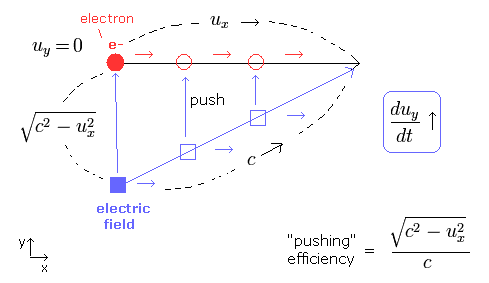
Fig.4 では、 電場は 電子を y 方向へ加速させようとしている。
これをするには、電場が 電子と同じ速度で x 方向へ進みながら 電子を y 方向へ押す (push) ことになる。
電場のスピードは c であるため、"押す" 効率 (= "pushing" efficiency ) は Fig.4 に示すようになる。
( 電子の速度 u_x がゼロのとき、　この 押す効率は c/c = "1" となる。)

結果として、Eq.49 の重くなる電子の質量効果を説明することができた。
この効果を一般化すれば、Eq.47 の運動量が得られる。

重要な点は ボーア・ゾンマーフェルト模型は １次のエネルギー項を用いており、W = 運動エネルギー＋位置エネルギー を "定数" として扱っていることである。 ( Eq.25 も参照のこと。)
実は、特殊相対論の ２次のエネルギーの式は 各粒子のエネルギーや運動量の 足し算、引き算が正常に行えないのである。
( このページ の "相対論的な ＱＥＤ が 特殊相対論と矛盾する？？" を参照のこと。)
そのため、相対論では "仮想粒子"のような 奇妙な概念を導入せざるを得なかった。

------------------------------------------------------------------------------

ここで次のような置き換えをする。
(Eq.50)

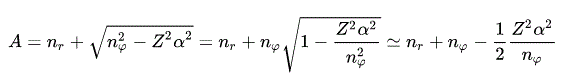
Eq.50 を Eq.39 に代入して、Eq.39 のテイラー展開は次のようになる。
(Eq.51)

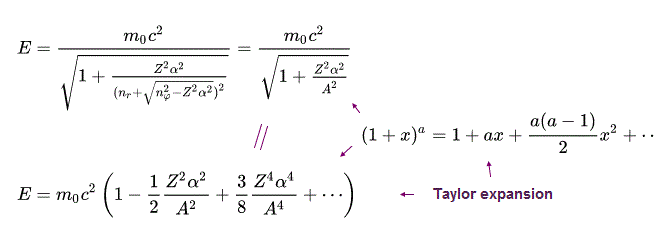
つまり、全エネルギー W は 次のようになる。
(Eq.52)

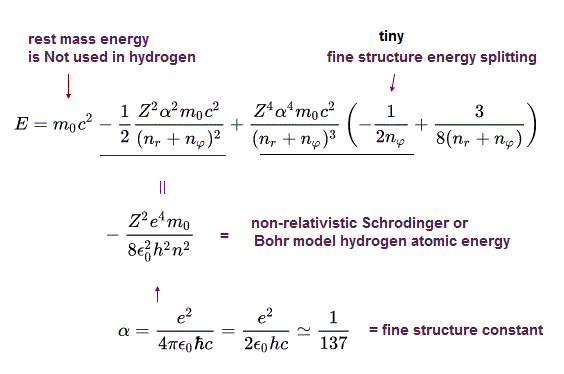
微細構造定数 α は 小さい。
そのため、Eq.50 の A を n_r+n_φ と仮定すると、Eq.52 の最初の項は 非相対論的なボーア・ゾンマーフェルト模型（もしくは シュレディンガー方程式）の解とちょうど同じになる。
（このページ も参照のこと。）
(Eq.53)

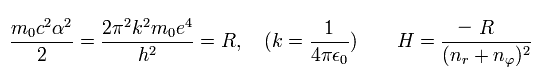
Eq.50 と 微細構造定数 α を使って、1/A² は次のように表せる。
(Eq.54)

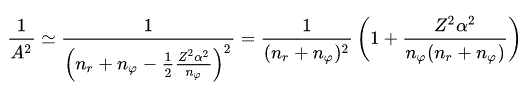
α は小さいので、近似的に 1/A⁴ を次のようにする。
(Eq.55)

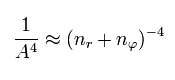
Eq.53, Eq.54, Eq.55 を使って、Eq.52 の W は次のように表せる。（α⁴ の近似で。）
(Eq.56)

例えば、Eq.57 を Eq.56 に代入すると、（Eq.23, Eq.53 も使って） ボーア・ゾンマーフェルト模型の 2s と 2p のエネルギーの違い は Eq.58 のようになる。
(Eq.57)

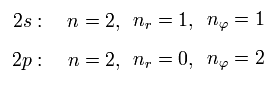
(Eq.58)

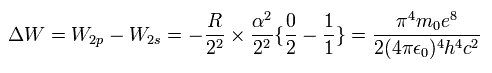
ゾンマーフェルト理論によれば、エネルギー準位 n の中の 角運動量量子数が k と k-1 である軌道のエネルギー準位の違いは Eq.59 のようになる。
(朝永著 「スピンはめぐる。」 も参照のこと。)
(Eq.59)

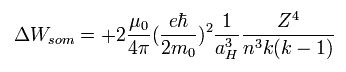
もし、2s と 2p の間のエネルギーの差を知りたいときは、Eq.59 に n=2 と k=2 を代入する。
(2s -- n=2, (k-1)=1,   2p -- n=2, k=2)

ここで a_H は ボーア半径 で、μ₀ は 真空の透磁率 である。
そのため、それらは次の関係式であらわせる。
(Eq.60)

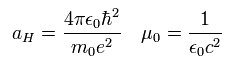
Eq.59 は H, He+, Li++, Be+++ などの 様々な原子の微細構造の実験値に よく一致することが分かっている。

ここで、Eq.59 を計算する。( Z=1, n=2, k=2 代入して。)
(Eq.61)

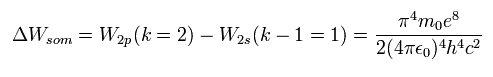
Eq.61 は Eq.58 に ちょうど等しくなる。
これは、Eq.59 と Eq.56 は同じ式であることを意味する。

トーマス歳差因子とパウリの御裁可。

このページに示したように、スピンする電子の角運動量を 1/2 ħ にするには、電子球面の速度が 何と 光速の 100倍 以上に ならなければならない。
そのため、1920 年代に パウリは 電子スピンの存在に対して とても強く反対した。

当時は、ゾンマーフェルトの Eq.59 の式が 様々な原子の実験値に合致することが知られていた。
(Eq.59)

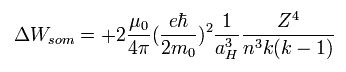
電子スピンの存在を証明するには、相対論的な質量変化によってではなく、スピン・軌道相互作用 によって Eq.59 の式に到達する必要があった。

ここで 電子が +Ze の原子核の周囲を周回していると仮定する。
すると、動いている電子の視点からすれば かわりに 原子核が電子の周囲を周回していることになる。
原子核の速度は -v、また 原子核の座標は -r である。
そのため、ビオ・サバールの法則によれば、電子の地点に生じる 磁場 (B) は次のようになる。
(Eq.62)

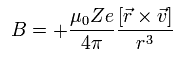
ここで 角運動量量子数 K (K = 1, 2, 3 ....) を導入する。
この K は K ħ = m₀r × v の関係式を満たす。
そのため Eq.62 は 次のように表せる。
(Eq.63)

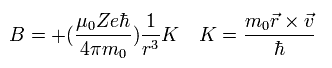
スピンする電子の 磁気モーメント は ｇ因子 (g_e) × s (=1/2) × ボーア磁子 である。
そのため スピンする電子と 磁場 (B) との間の 相互作用エネルギー は次のようになる。
(Eq.64)

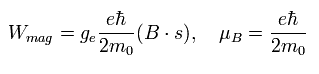
ここで μ_B は ボーア磁子, s はスピン角運動量 (=1/2) である。

Eq.63 の B を Eq.64 に代入する。
(Eq.65)

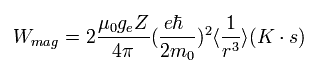
Eq.65 の spin up (+1/2) と spin down (-1/2) の間の エネルギー準位の差 は次のようになる。
(+1/2 - (-1/2) = 1)
(Eq.66)

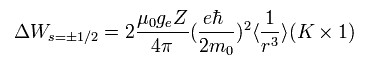
ボーアの理論によれば、1/r³ の平均値は 次の関係式を満たす。
(Eq.67)

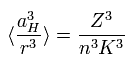
ここで a_H は ボーア半径、 n は エネルギー準位を表す。

Eq.67 を Eq.66 に代入する。
(Eq.68)

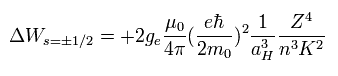
ここで Eq.68 の K² を k(k-1) に変換すると、実験値に よく合うことが知られていた。
(Eq.69)

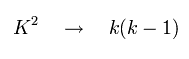
Eq.69 を Eq.68 に代入する。
(Eq.70)

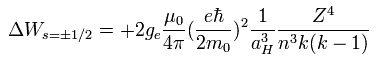
ここで スピンｇ因子 (g_e) が 1 だとすると、Eq.70 は Eq.59 (= ゾンマーフェルト模型) に ちょうど一致する。
しかし、もし g_e が 1 だとすると、電子の磁気モーメント は 1/2 × 1 = 1/2 × ボーア磁子 になってしまう。
つまり、Eq.70 は間違っていることになる。 なぜなら 電子の磁気モーメント (磁気能率) は 1 × ボーア磁子 にならなければならないからである。

この問題を解決するために トーマス (L.H. Thomas) が登場した。
彼は、トーマス因子 1/2 を使うことにより、電子スピンの正当化に成功した。
(しかし、トーマスの方法は 少々複雑で、不自然なものと言わざるをえないが。)
次に この因子について説明することにする。

このページ に示したように 磁場 (B) のもとでの スピンする電子の 歳差運動の角振動数は 次のようになる。
(Eq.71)

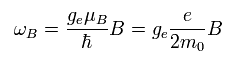
ボーアの 対応原理 によれば、ħω = | W₁ - W₂ | である。
ここで Eq.71 に ħ をかける。
(Eq.72)

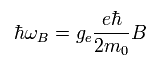
Eq.64 に示したように 磁場 (B) のもとでの 相互作用エネルギーは、
(Eq.64)

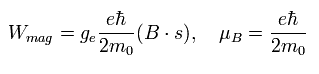
であり、磁場のもとでの ２つのスピン状態 s = ± 1/2 の間のエネルギー差は、
(Eq.73)

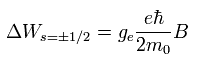
である。Eq.73 は Eq.72 と等しくなる。

トーマスは、電子が"加速度運動" しているとき、電子の"固有の"座標系 は 実験室系に対して 回転していることに気づいた。
彼の計算結果によれば、この座標系の回転角振動数は次のようになる。
(Eq.74)

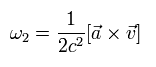
ここで、a は 電子の 加速度 である。

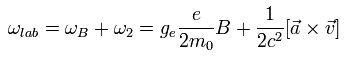
電子の加速度は 次のような +Ze の原子核のクーロン力によって生じる。
(Eq.76)

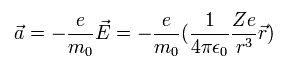
ここでは Eq.62 と Eq.60 の μ₀ を使う。
(Eq.62)

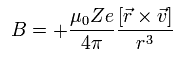
Eq.76, Eq.62, Eq.60 から、Eq.75 の全角振動数は次のようにあらわせる。
(Eq.77)

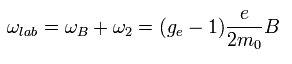
Eq.77 を使うと、Eq.64 の 磁場のもとでの 相互作用エネルギーは 次のように変化する。
(Eq.78)

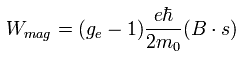
また、Eq.70 は 次のように変化する。
(Eq.79)

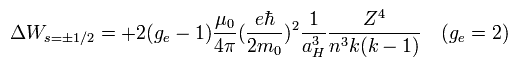
g_e が 2 のとき、Eq.79 は ボーア・ゾンマーフェルト模型の Eq.59 とちょうど等しくなった！

Eq.79 = 1/2 × Eq.64.
そのため、この 1/2 を "トーマスの歳差因子" と呼ぶ。

これによって ようやく パウリは トーマスのスピン模型を "しぶしぶ" 受け入れることとなった。
(ようやく、トーマスは 電子スピンに関して パウリの御裁可を得ることができたのだ。)

ところで、トーマスのスピン・軌道相互作用モデルと ボーア・ゾンマーフェルトモデル、はたしてどっちが より自然な微細構造 だと みなさんは思われたことだろうか？
もし、微細構造が スピン・軌道相互作用によって生じるとしたら、このモデルは 相対性 と スピン・軌道相互作用 の ”たくさんの不自然な偶然の一致”を 含まなければならない。　( 2S_1/2=2P_1/2, 3S_1/2=3P_1/2, 3P_3/2=3D_3/2.........).

また Eq.69 の置き換え ( K² → k(k-1) ) は Eq.59 のボーア・ゾンマーフェルト模型においては "自然に" 得ることができた。
しかし、スピン・軌道 相互作用模型 においては、Eq.69 の置き換えは 量子力学的な l (l+1) という "数学的技巧" に頼らなければならない。

また、Eq.72 のボーアの対応原理の利用も奇妙である。
1975 年の スピンの２価性の実験によれば、フェルミ粒子は １回転で元に戻れない。(２回転で元に戻る。)
そのため、電子スピンに関しては、4π の角度を 1 振動とみなすべきである。
こうすると、Eq.72 の角振動数は 半分 になることになる。
しかし、Eq.72 が半分になると、せっかくの トーマス因子 1/2 が 無意味 になってしまう。
つまり、この模型は自己矛盾を含んでいることになる。

結論として、スピン・軌道相互作用模型は、ボーア・ゾンマーフェルト模型に比べて、非常に無理強いした 不自然な模型と言わざるを得ない。

ペニング・トラップによる異常磁気能率の測定。

最近では、１つの電子をトラップできる ペニング・トラップ (Penning trap) を用いて [3]、異常磁気能率の測定が行われた。

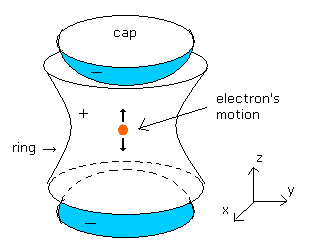
Fig.5 に示すように、ペニング・トラップは 上下の部分に 負電荷に帯電した キャップ (cap) がついている。
また、側面周囲には 正電荷に帯電した リング (ring) がついている。

中心を原点とすると、ペニング・トラップの 電位 は次のようになる。
(Eq.80)

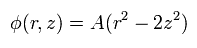
つまり、電子は次の力によって、ｚ方向に 原点のほうへ引き戻されている。
(Eq.81)

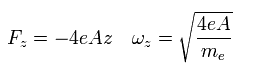
ここで ω_z は ｚ方向の角振動数である。

また、電子は 正電荷のリングに外側方向へひきつけられる。
そこで、ｚ方向に 磁場 (B₀) をかける。
すると、x-y 平面上の 電子の運動方程式は 次のようになる。
(Eq.82)

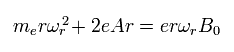
Eq.82 は 遠心力とローレンツ力を含んでいる。

さらに 次のような 小さな磁場をかける。
(Eq.83)

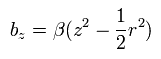
Eq.83 の磁場勾配のため、電子の磁気モーメントは次の力を受ける。
(Eq.84)

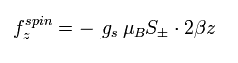
ここで μ_B は ボーア磁子で、S はスピン角運動量 (± 1/2)、g_s は スピンｇ因子である。
(Eq.85) ボーア磁子。

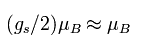
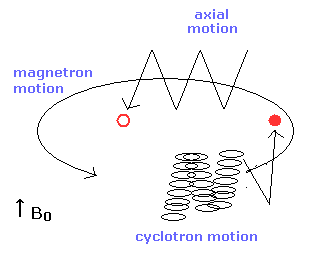
ペニング・トラップでは、Fig.6 に示すような 様々な運動が混在している。
そのため、電子の運動は とても複雑になっている。
もちろん、電子はとても軽いため、熱雑音の影響もとても大きい。

(Fig.6) ペニング・トラップにおける 軸方向運動、磁場運動、サイクロトロン運動。

様々な量子数のサイクロトロン運動に及ぼす 磁気的な力は 次のようになる。
(Eq.86)

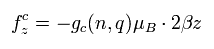
結果的に、ｚ方向の全角振動数は次のようになる。
(Eq.87)

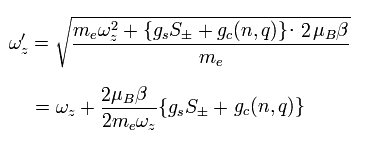
さらに、ここに 弱い振動電位 ( V =K sin ω t ) をかける。
この ω が Eq.87 に等しいとき、それは "共鳴"を起こす。
また この ω は測定できる。

電子のスピンは ランダムに 上下に変化 (flip) している。
（もちろん、様々なサイクロトロン運動もランダムに変化している。）
彼らは、Eq.87 の ± S の間の 角振動数の差 と思われるものをその中から 選びだし、 測定する。
そして、スピンｇ因子の値を得ることができる [4]。

しかし、Eq.88 に示したように、最小の (= ħ) 軌道運動 によって生じる 磁気モーメントも スピン磁気モーメントと同じである。
(Eq.88)

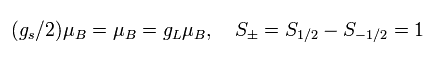
つまり、”奇妙な”スピンのかわりに、最小の軌道運動を用いると、ｇ因子は 半分になる。
(”解釈”だけが変わるだけである。)

( References )
[1] W.H.Louisell, R.W.Pidd, An Experiment of the Gyomagnetic Ratio of the Free Electron, Phys.Rev.94 (1954) 7-16.
[2] D.T.Wilkinson, H.R.Crane, Precision Measurement of the g Factor of the Free Electron, Phys.Rev.130 (1963) 852-863.
[3] Dehmelt, Experiment with an Individual Atomic Particle at Rest in Free Space, Am.J.Phys.58 (1990) 17-27.
[4] H.Dehmelt, New Continuous Stern-Gerlach Effect and a Hint of the Elementary Particle, Z.Phys.D10 (1988) 127-134.
[5] V.Gerginov, K.Calkins, et.al. Phys.Rev. A 73 (2006) 032504.

2011/2/4 updated This site is link free.