トップページ (2電子原子も含む正確な新ボーア模型)
様々なスピン理論は スピンを意味しない。
微細構造=スピン軌道は 間違い。
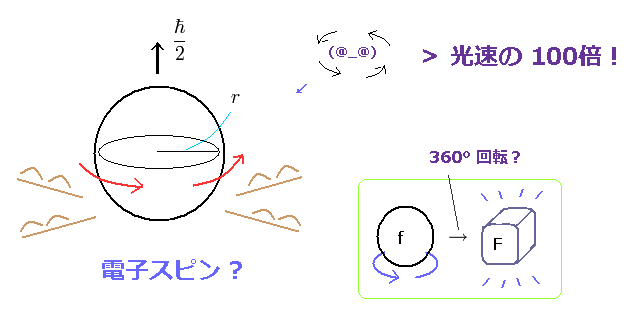
(Fig.1) スピン速度は超光速 ! → 電子スピンは 幻想である。

通常の教科書は "スピン" を 実在のもののように 扱っているが、電子スピンには 完全に リアリティーがない。
電子は 非常に軽く また小さい。
そのため、角運動量 1/2 ħ を出すには、電子表面のスピードが何と光速の100倍以上にならないといけないのである ( ウェブサイト ここ p.5, ここ )。
さらに 電子などのフェルミ粒子は 360o の回転で 元に戻ることができないのである。 このサイト参照のこと。
この時点で 電子スピンが この世の現実の概念でないことが 容易に理解されたことと思われる。
(Fig.2) 角運動量が定数のとき、小さい粒子ほど スピン速度が速い。
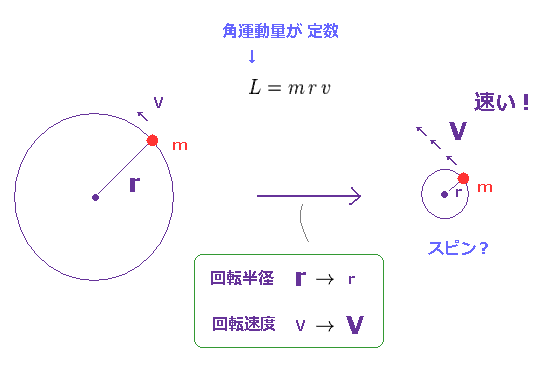
角運動量は L = mrv で与えられ、 ここでは "m" が 質量、 "r" は 半径であり、 "v" は 接線方向の速度である。
この角運動量が 定数の決まった値のとき、回転速度は 半径が小さくなるほど 速くなる。
(Fig.3) 小さな電子では、スピン速度は 光速を大きく上回る。
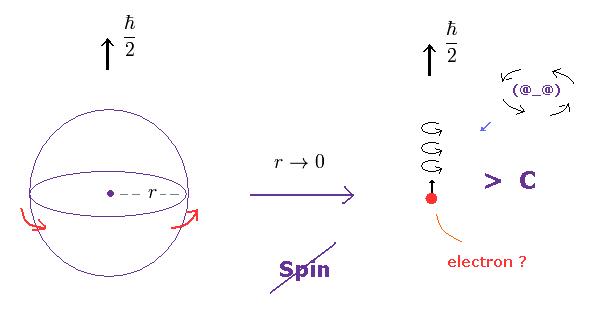
電子は 点状粒子であるため、その半径は 非常に小さい。
しかし 現在の量子論では この電子が 1/2ħ という 決まったスピン角運動量を持つことになっている。
結果的に、その回転スピードは 光速を はるかに超えてしまうことになる。
(Fig.3') スピン速度は 光速の何百倍も速い。
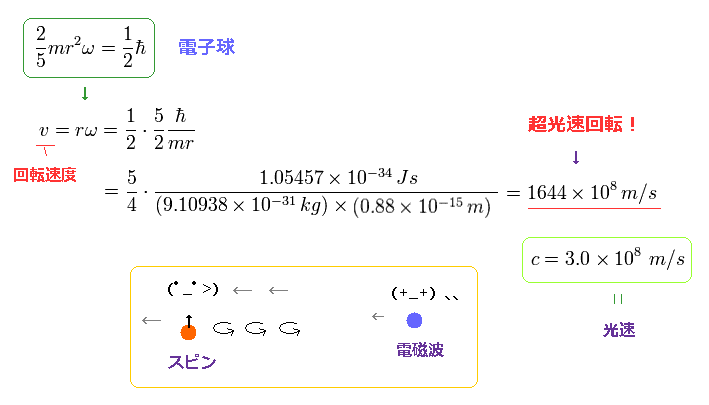
この事実より 電子スピンというものが 現実的な概念でないことが 容易に理解できたと思われる。
このことが 1920年代に 当初 パウリが 電子スピンという概念に 頑なに反対していた理由である。
(Fig.4) 陽子のスピンは 大丈夫。 電子スピンは存在しない。
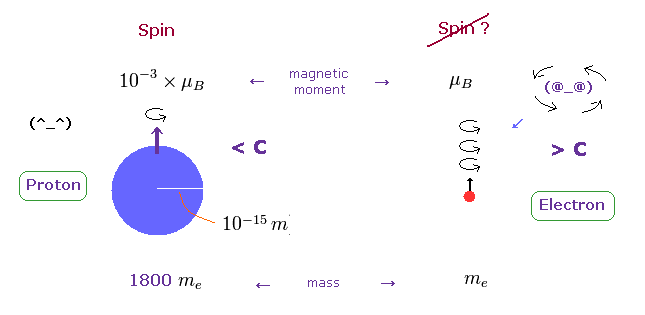
一方で、一定の大きさのある重い陽子は 光速を越えることなく "本当の" スピン回転をすることができる。
つまり 原子核のスピンは リアルであり、電子スピンは 実在しないということになる。それは ボーア模型のように スピンでなく 単に 円軌道上の運動であることを示している。
実際、電子スピンの磁気モーメントは 陽子の磁気モーメントの 1000 倍以上もの強さがある。同じスピン、電荷なのに違いすぎである。
この 極端な相違は 電子スピンが ある大きさの半径の円軌道運動によって生じ、自身の自転によるものでないことの証しである。
(Fig.5) フェルミ粒子は 2回転 (= 720o ) しないと 元に戻らない。
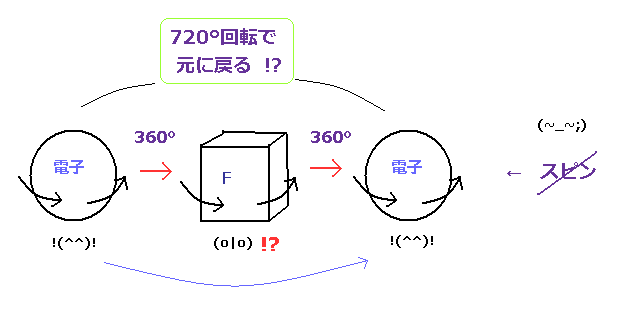
量子力学によれば、スピノル (= スピンする電子 ) は 一回転 ( 360o ) しただけでは 元に戻れないのである。
元に戻るには 2回転 (= 720o ) しなければならない。 このサイト参照のこと。
これを スピノルの "二価性" という。
驚くことに、量子力学は 電子、中性子、陽子の すべてのフェルミ粒子が 1回転 (= 360o ) で元に戻らないと主張しているのである。
(Fig.6) フェルミ粒子は 2回転 (= 720o ) しないと 戻れない。
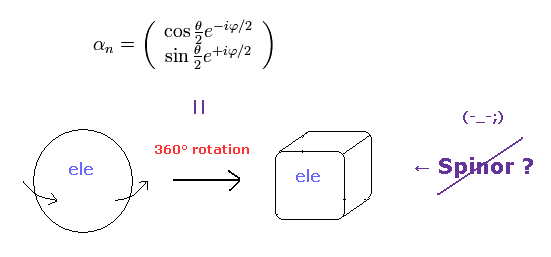
スピン角運動量 1/2ħ を考慮すると、スピノルの波動関数は Fig.6 のようになる。
360o ( θ = 0 → 360o ) 回転では、このスピノルの値が変化してしまう。
つまり、フェルミ粒子を表す スピノルは 現実のものでは ない のである。
驚くことに、 このセクションにあるように、 この奇妙な現象が
現実の実験で 確認されたことになっているのである。
もちろん、現実の物が 1回転で元に戻ることは 当たり前のことである。
これらの実験のトリックは 角運動量の 誤った前提条件に ある。
(Fig.7) スピノル は 皿 か 紐 ? 不可能。
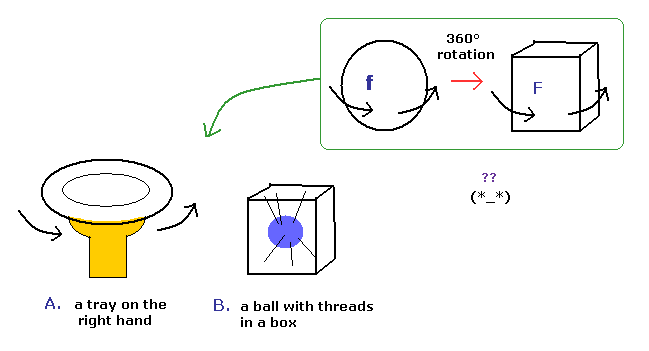
様々な人たちが この奇妙なスピノルを 実際の物を使って 表わそうとしてきた。
Fig.7A は 手のひらに お皿がある状態。 Fig.7B は 箱の中に ボールと紐が つながれている状態である。しかし、欠点は あらゆる方向の回転を考えると、腕や紐が絡まってしまい、おかしくなることである。
つまり、スピノル回転自体は 現実のものでは 表わすことができないのである。
(Fig.8) ボーア軌道 = ボーア磁子 スピン = ボーア磁子
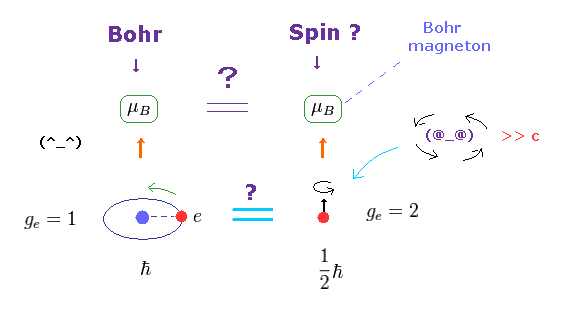
ボーア磁子 (= μB ) の大きさの磁気モーメントは このサイトにあるように 最初は ボーア軌道において定義された。
驚くことに、本来まったく関係のない スピン磁気モーメントまでも このボーア磁子と 同じ磁気モーメントを持っているのである。 このサイト参照のこと。
軌道運動と "スピン" は 異なった概念同士なのに 奇妙としか言いようがない。
磁気モーメントは g-因子 × 角運動量 で与えられる。
ボーア軌道では、 g-因子 = 1 で 角運動量 = ħ である。
電子スピンでは、 g-因子 = 2 で 角運動量 = 1/2ħ である。
結果 これらの値は まったく同じになるという訳である。
あまりにも出来すぎである。
(Fig.9) シュテルン・ゲルラッハの実験 = ボーア軌道。
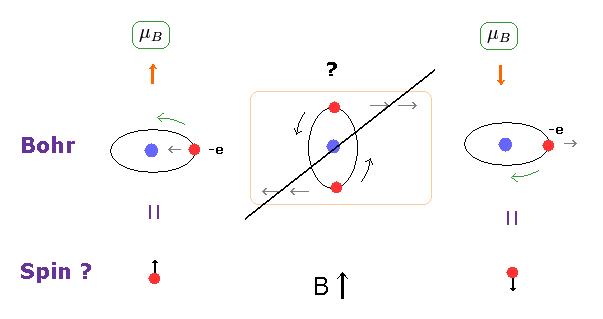
シュテルン-ゲルラッハの実験は スピン の証明をしたと言われている。
しかし実は、ボーア軌道も この現象を 自然に説明することができる。
Fig.9 真ん中を見て分かるように、軌道面が 磁場 B に 平行のとき、この平面は 回転する傾向にある。
つまり ボーア軌道においても シュテルン・ゲルラッハの実験で 2つに分かれる線を 観測できるのである。
Fig.8 に示したように、ボーア軌道と 電子スピンの両方において 磁気モーメントの大きさは ボーア磁子である。
それらにおいて 分裂間隔は 同じになる。 スピンとは 非常に出来すぎの概念である。
(Fig.10) 磁気モーメント。
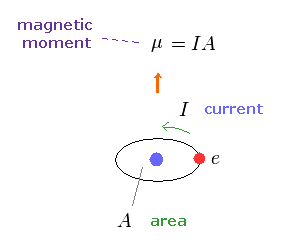
このサイトにあるように、磁気モーメント μ は 電流 I × その回路の面積 (= A ) で与えられる。
この磁気モーメントは 2つの正反対の磁荷からなる双極子と 同じ磁場を与える。
そのため これを "磁気双極子モーメント" と呼ぶ。
(Fig.11)
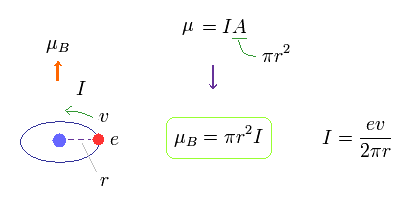
Fig.11 では、1つの電荷が 速度 "v" で 軌道運動している。
この軌道半径を "r" とする。
電流 I とは ある地点を 毎秒通過する 電荷量を意味する。
つまり I は ev/2πr で与えられる。
この円形回路の面積は A = πr2 であるため、 磁気モーメントは μB = IA = Iπr2 になる。
(Eq.1) 軌道長が 1 × ドブロイ波長のとき・・。
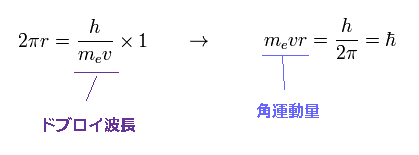
ドブロイ理論によれば、電子の波長は λ = h/mv という式で与えられる。
Eq.1 は 軌道長 (= 2πr ) が このドブロイ波長に ちょうど等しいときである。
この場合、軌道角運動量 (= mvr ) は ħ になる。
Fig.11 と Eq.1 から、磁気モーメント μB は、
(Eq.2) ボーア磁子。
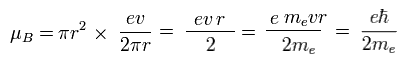
この磁気モーメントの値を "ボーア磁子" と呼ぶ。
ボーア磁子は 現在の量子力学においても 磁気モーメントの単位として 非常に重要な概念である。
つまり、 ドブロイ波長の量子化が 磁気モーメントの量子化を引き起こす 主要なメカニズムなのである。
(Fig.12) スピン g因子 = 2 ??
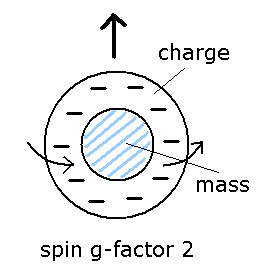
Fig.8 で述べたように、スピン角運動量は 1/2ħ であるため、 ボーア磁子を与えるには スピンg因子は "2" にならなければならない ( 1 = 1/2 × 2, Eq.3 参照 )。
ところで、このスピンg因子の 本当の意味とは何なのだろうか?
通常の古典力学では、g因子は 必ず "1" になる。
そのため、g因子 "2" では、Fig.12 に示したように、電荷と質量が 分離していなければならない。
(Eq.3) スピン磁気モーメント = ボーア磁子。
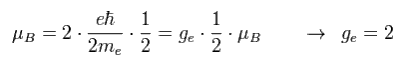
それなら、どうしてこのスピンg因子は "2.3", "2.4", "2.7" ... のような中途半端な値でないのだろうか?
当たり前のように ちょうど "2" という値に設定したところが 非常に 出来すぎた概念だと思われないだろうか?
(Fig.13) スピン磁気モーメントは 弱すぎで ナトリウムの D-線 を説明できない。
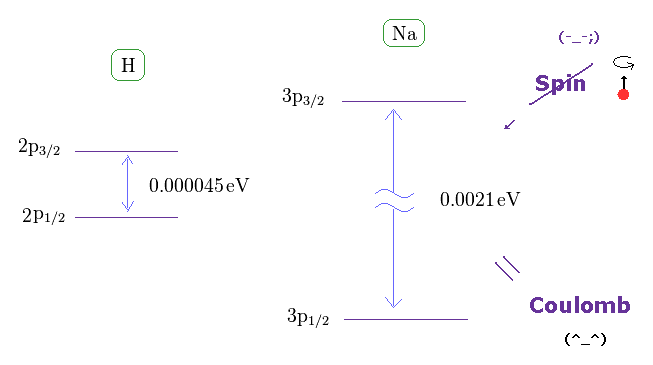
このサイトにあるように、水素の 2p3/2 と 2p1/2 準位間の 微細構造 (= 2重項 ) は 約 0.000045 eV である。
一方で、ナトリウムの 3p3/2 と 3p1/2 準位間の 微細構造は 0.0021 eV もある。 このサイトも参照のこと。
もし 水素の2重項が スピン・軌道相互作用によると仮定すると、 ナトリウムの2重項が、スピン・軌道相互作用で 説明できなくなってしまう。 このページ参照のこと。
微細構造において、 ゾンマーフェルト模型と ディラック方程式は 同じ値を与えることが知られている。
水素とナトリウムの 2重項で 同一のメカニズムが 働いていると仮定すれば、 微細構造は ゾンマーフェルト模型のように 1つの電子が もう1つの電子よりも 原子核に より近づくことによって生じる エネルギー差であると 自然に見なせる。
(Fig.14) ナトリウムの 芯部分の電荷は Z = 1 よりも はるかに大きい !?
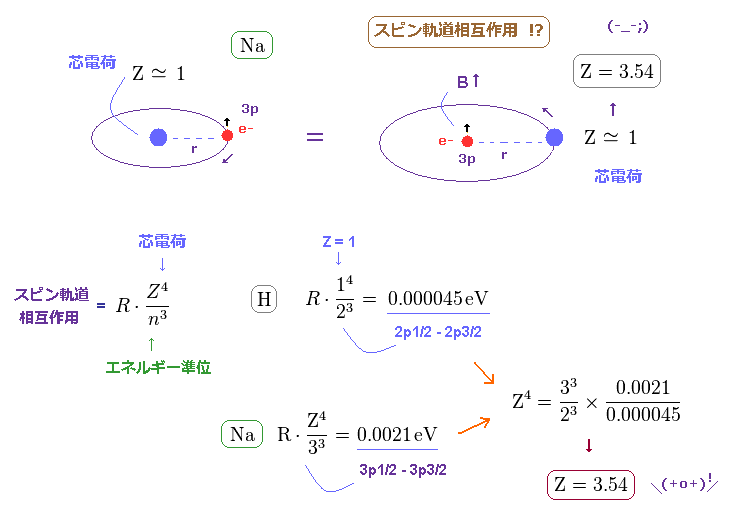
近似的に、ナトリウムの 3p ( もしくは 3s ) 準位の電子は Z = +1 の中心の芯の部分の電荷の周囲を 回っていると見なせる。
( "芯の部分" とは Na の原子核と n=1 と n=2 の軌道に含まれる すべての電子の合計の電荷の意味である。 )
この外殻電子からの視点では、中心の芯電荷は 逆方向に回っており、スピンを持つ電子の部分に 磁場を生じさせることになる。
結果的に スピン・軌道相互作用が生じると彼らは主張している。
しかし これらの H と Na のスピン軌道相互作用間の違いは あまりにも大きい。
これはつまり ナトリウムにおける 有効中心電荷は Z = 1 よりも はるかに大きくなければならない ( Na で Z = 3.54 ぐらいになってしまう )。
この結果は 現実のナトリウム原子の観点からして あまりにも非現実的で 不合理である。
(Fig.11) 水素原子の異常ゼーマン効果? ↓ = ボーア・ゾンマーフェルト模型。
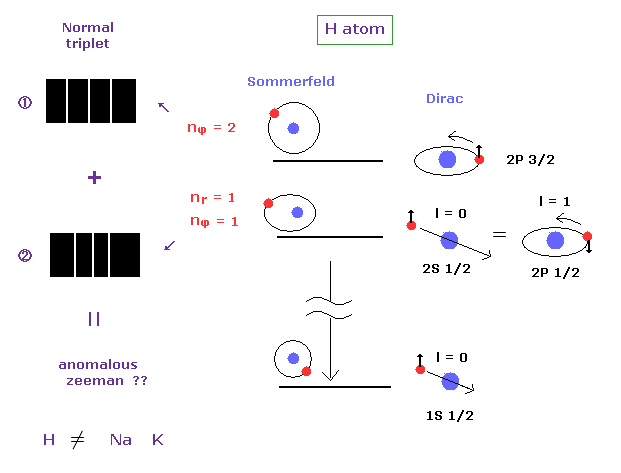
異常ゼーマン効果は 主に アルカリ金属で 観測され、 上で述べたように それは 実際のエネルギー間隔と 一致しない。
実際、水素原子のスペクトル線は 非常に単純で、ボーア・ゾンマーフェルト模型で 水素原子の異常ゼーマン効果を説明できる。
(Fig.16) J Mehra's のテキスト。

量子力学の誕生に至る歴史を語った本、 Historical Development of Quantum Theory v.1 part2 ( J. Mehra ) の 659 ページには次のように書いてある。
--------------------------------
1922 年、 Otto Oldenberg は 次のような結果を得た。
弱い磁場のもとでは、バルマー系列の Hα の 2重項の各ラインが 正常ゼーマン効果の 3つの準位に分離し、 強い磁場のもとでは、 2重項のゼーマンパターンが 1重項のゼーマンパターンに変化した。
---------------------------------
つまり、水素原子における これら2重項 (= 2 × トリプレット )を "異常ゼーマン効果" と 呼んでいるだけなのである。
もうご存じのとおり、これら2重項 (= 微細構造 ) は 奇妙な "スピン" に頼らずとも、ボーア・ゾンマーフェルト模型で 完全に 説明可能なのである。
(Fig.17) ゼーマン効果の歴史。

上記のテキストによれば、異常ゼーマン効果は Na, Cd, Mg などの 多電子原子に 主として見られたと書いてある。
水銀 (= Hg ) では 1898 年に 磁場のもとで 11 ラインもに分離するのが確認された。
重要な点は 異常ゼーマン効果について語るとき、基本的に 水素原子には まず 触れない ということである。
( こういうとき、便利な パッシェン・バック効果という概念を導入した。 )
そのため 当時、ハイゼンベルグや ランデは 異常ゼーマン効果は スピンでなく内殻の電子群によって生じると 最初 考えていたぐらいである。
また 様々な原子や金属は ランデのg因子に 従わないのである。
この事実が ラッセルやサンダーズに jj, jk カップリングなどの 人為的な概念を創出させる動機となった。
ランデのg因子の計算に関しては、 このセクションを参照のこと。
(Fig.18) マグネシウム (= Mg ) の 1、3重項 は "スピン" でなく、クーロン相互作用による。
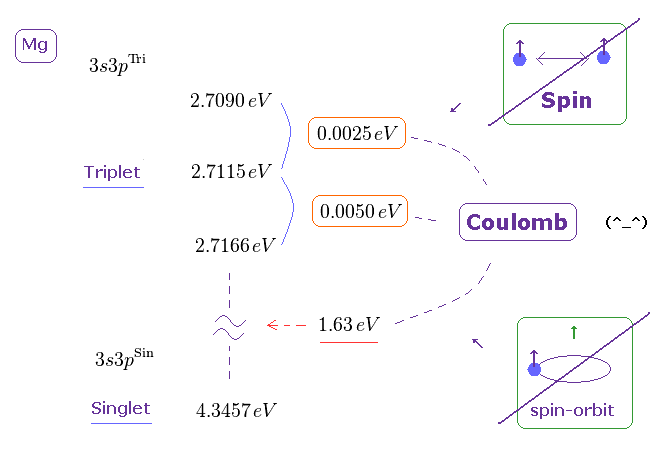
現在の量子論によれば、アルカリ土類金属の "1重項"、"3重項" は、
スピン・スピン もしくは スピン軌道相互作用によって生じるとしている。
しかし実は、1重項、3重項のエネルギー分裂の間隔は スピン間の磁気エネルギーによる計算値よりも はるかに大きいのである。 このページ参照のこと。
( 朝永振一郎の "スピンはめぐる" には それらは 電気的な力 (= クーロン力 ) に起因すると書いてある。 )
なぜなら、スピン・スピン磁気相互作用エネルギーは 弱すぎて (= 1 × 10-4 eV 未満 ), とても 1、3重項のエネルギー間隔の大きさに 届かないのである。 このサイト (p.6) や このサイト (p.7) 参照のこと。
(Fig.19) 相対論効果に基づく スピン・軌道相互作用は 弱すぎる。
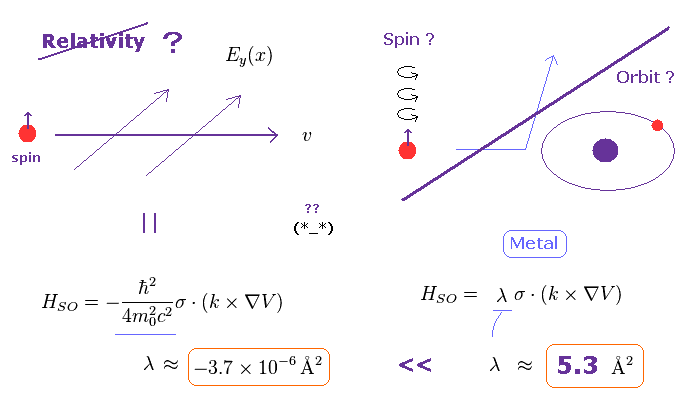
現在の理論によれば スピン軌道相互作用は 相対論効果によって生じるとされている。
(= ウィキ 参照のこと )。
しかし そうだとすると スピン・軌道相互作用の大きさが 実験値よりも はるかに 小さくなってしまうのである。
( このサイト、
このサイト (最後のほう)、
このサイト p.6 など参照のこと )。
この論文 ( p.2, 左 ) には 以下のように書かれてある。
-----------------------------------
"例えば GaAs では、結合定数 λ = 5.3 Å2 となる。
つまり n-GaAs における スピン軌道相互作用は 真空中の値 ( λ = -3.7 × 10-6 Å2 ) よりも 6桁ほども 強いことを意味している。また その符号も 反対である。
この スピン軌道相互作用の増強は 外因性のスピン流の形成という考えに必須である。
------------------------------------
結合定数 λ における この あまりにも大きな解離は このページに示したように、 スピン・軌道相互作用という概念自体が 完全に 架空 のものであることを示している。
(Fig.20) スピン磁気モーメントは 弱すぎて パウリの排他原理を説明できない。
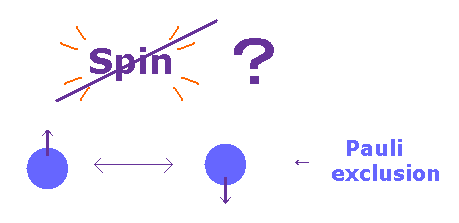
パウリの排他原理によれば、2つの電子は 軌道とスピンに関して 同一の状態になることができない。
通常の教科書は この現象は スピン・スピン相互作用によると 当たり前のように 説明している。
しかし パウリの排他原理の大きさは 10 eV ほどもあり、非常に弱いスピン磁気モーメント ( 〜 10-5 eV ) では、到底 説明することができない。
(Fig.21) パウリの排他原理の反発力は かなり強い (= リチウムで 約 11 eV ).
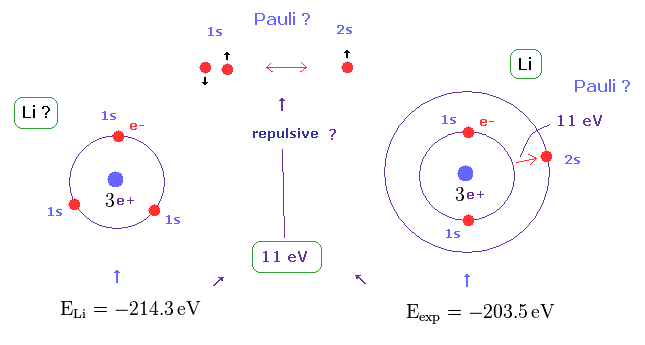
リチウムの 3番目の電子は 2s 軌道にあるが、もし リチウムの3つすべての電子が 2s よりも はるかに原子核に近い 1s 軌道に存在すると、基底状態のエネルギーが -214.3 eV 未満になり、これは 実験値 -203.5 eV よりも低くなってしまう。( Quantum chemistry 6th, Ira N. Levine, p 292 )
つまり、実験値に合うには 3つ目の電子が 原子核の 強いクーロン引力に打ち勝って 1s から 2s に押し出す反発力が必要になる。この大きさは 上記の差で 約 11 eV ぐらいになる。
(Fig.22) スピン・スピン相互作用は 弱すぎる。
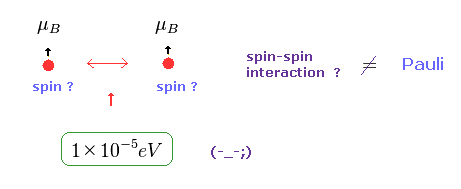
パウリの排他原理では 互いのスピンの向きの関係で その軌道に入れるかどうかが決まるため、あたかもスピン磁気モーメントの相互作用が この 11 eV の反発力の源のように錯覚しやすい。
しかし 計算してもらうとわかるが この 磁気双極子相互作用というのは 微細構造ぐらい ( 1 × 10-5 eV ) の大きさぐらいしかなく、 とてもじゃないが クーロン力に対抗できるものではない。
つまり このパウリの排他原理の強力な反発力を説明するには 別の何かの力を借りなければならない。
スピン磁気モーメントが弱すぎて役に立たないとすれば 残りは1つしかない。
このページに示したように ドブロイ波の干渉作用が パウリの反発力の原動力と考えると しっくりくる。
(Fig.23) 強磁性の起源 = スピン ?
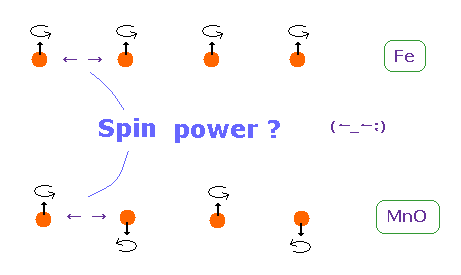
強磁性では、鉄などの 各スピンが 互いに平行に揃うことによって生じるとされている。
一方、 MnO などの 反強磁性では 各スピンが 互いに 反平行になるように相互作用するとしている。
ということは、(反)強磁性の 起源 は 多くの教科書が言うように "スピン" ということになるのだろうか?
実は、スピン磁気モーメント間の相互作用というのは 強磁性などを引き起こすには、
これもまた 余りにも弱すぎるのである。
(Fig.24) 強磁性の起源 = 交換相互作用 "J" ?
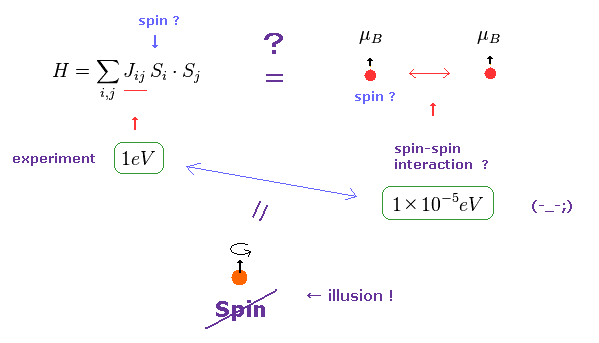
現在の量子論では (反)強磁性の力を ハイゼンベルク模型の 結合定数 (= J ) で 表そうとしている。
この交換相互作用を表す結合定数は 1 eV ぐらいの大きさがあり、スピン・スピン磁気相互作用 (= 10-5 eV ) に比べて はるかに大きい。
つまり スピン磁気モーメントによる 相互作用は こういった磁性体を説明するには
桁が 小さすぎなのである。 (
このサイト や
このサイト も参照のこと。)
スピン磁気相互作用は 温度表示で 0.3 K しかなく、これは 室温の熱雑音で 容易に 壊れてしまう。
( 例えば、鉄は 1043 K ほどでも強磁性体になることができ、この温度は 0.3 K よりもはるかに大きい。 )
(Fig.25) ドブロイ波の相互作用が 強磁性の起源である。
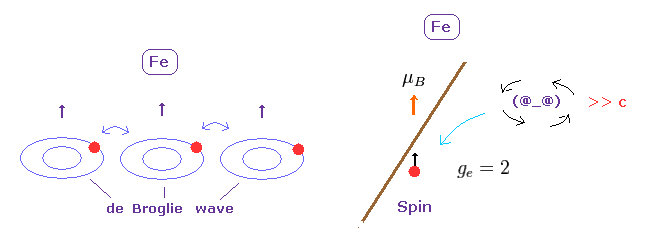
スピン・スピン磁気相互作用は 磁化を説明するには 非現実的なくらい 弱い。
ここでも 1つしか残っていない。
電子の軌道運動は ドブロイ波を伴う。 ( このページを参照のこと。 )
強いパウリの排他原理の反発力のように、これらの同調するドブロイ波が 強磁性を 室温で
安定 にさせていると考えるのが自然である。
ダビッソン・ガーマーの干渉実験に見られるように、ドブロイ波の干渉作用は クーロン力による散乱方向を変えるだけの力がある。
(Fig.26) スピンは 分子結合を説明するには 弱すぎる。
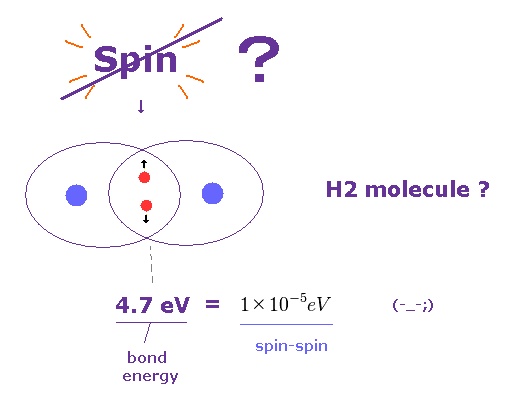
各分子結合は スピン アップとダウン の電子のペアを含んでいると言われている。
しかし 例えば 水素分子 (= H2 ) では、この分子間結合力は 4.7 eV にもなる。 このサイト参照のこと。
またもや スピン・スピン磁気相互作用 (= 10-5 eV ) は 弱すぎて これらの分子結合を説明することができない。
これらの間違った仮定を信じている限り、分子結合の 本当のメカニズムを 永遠に 解明することができない。
(Fig.27) "スピン" は ファンタジー?

この実験にあるように、 Fe の 高スピン、低スピン状態は "スピン"に関係しているという説明が多い。
しかし 鉄の 3d 電子は 非現実的なスピンとは 何の関係もないのである。
このサイトにあるように、 鉄の 3d軌道の 6つの電子が いくつかのサブレベルに分離している。
"t2g" 軌道は 基本的に 非結合であり、eg 軌道よりも 低いエネルギー準位にある。
この実験は これらの状態がどう変化するかを X 線を用いて調べたものである。
この図 を参照のこと。
(Fig.28) "スピン"磁気モーメントエネルギーは "弱すぎ"。

このサイト (Fig.15.1)にあるように、鉄における 高スピンと低スピン状態間のエネルギー差は 1 eV - 3 eV ほども離れており、これが 明らかに 非常に弱いスピン磁気相互作用でなく、 クーロンエネルギーによることを示している。
スピン磁気双極子作用は ボーア半径ほどの距離で 役 1 × 10-4 eV ほどしかない。 このサイト (p.6) や このサイト (p.7) 参照のこと。
Fe では、このスピン磁気エネルギーは さらに弱い (= 1 × 10-5 eV ほど ) ため、 1 eV のエネルギー差には 到底 及ばない。
この種の実験は 必ず 非常に曖昧な波動関数 ( 3d ) と 非現実的な スピン に頼っており、また このエネルギーの大きさが 実際の値と大きく食い違っている。
これらの曖昧な概念を捨てて より具体的な電子運動を定義しないかぎり、 分子結合の本当のメカニズムは 永遠に 分からないままである。
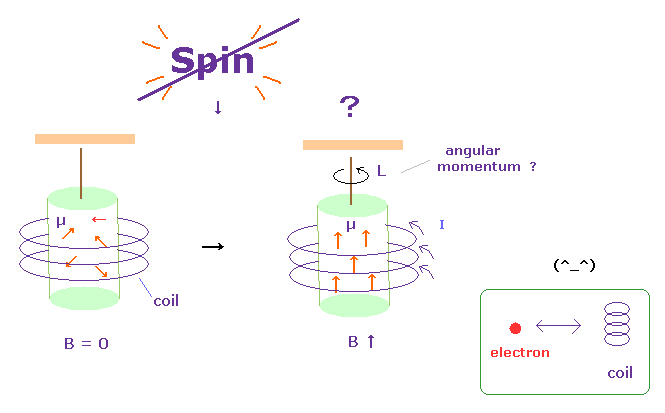
アインシュタイン - ド・ハース効果は "スピン" が "現実に回転していることを示したと言われている。
しかし スピンが 本当に回転だとすると、そのスピン速度は 上で 説明した通り、光速よりも はるかに速くなる必要がある。
これは奇妙である。
Fig.29 左図では、円柱内の 磁場 B は ゼロのため、磁気双極子モーメント (= μ ) は ランダムな方向を向いている。
Fig.29 右図では、磁場がかけられ、各 μ が 平行になり 円柱全体が 回転しだす。 このサイト p.4 や
このサイトを参照のこと。
彼らは この実験では 電子間の作用反作用を利用することにより、 スピンg因子 "2" が測定できたと主張している。
しかし このページにあるように、この実験では、 コイル内の電流が 電磁場という遠隔作用によって 原子の電子に影響を与えているだけの話である。
つまり 非現実的なスピンは この実験とは 何の関係もない。
(Fig.30) 波動関数と 非現実的なスピンが 主要な障害物。
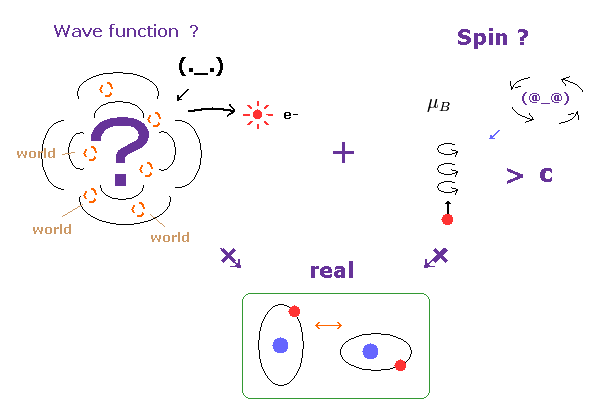
波動関数は 単に 粒子の曖昧な確率密度を与えるだけである。
つまり この曖昧な波動関数を用いて 粒子の具体的な運動を記述すること自体 到底不可能である。
この厳しい状況で、 非現実的なスピンのみが 具体的な ? もの として残ってしまった。
すでに述べたように、このスピン磁気モーメントは 重要な実験値を
まったく説明できない。
結果的に 現在の量子力学に基づく研究は 架空のものに依存しているため、
まったく 本質から遠ざかった方向へ進んでしまっている。
具体的な粒子の運動を認めない限り、生物学的なミクロの世界は 永遠に 謎のままである。
(Fig.31) 遷移スペクトル線の解釈は 非常におかしい。
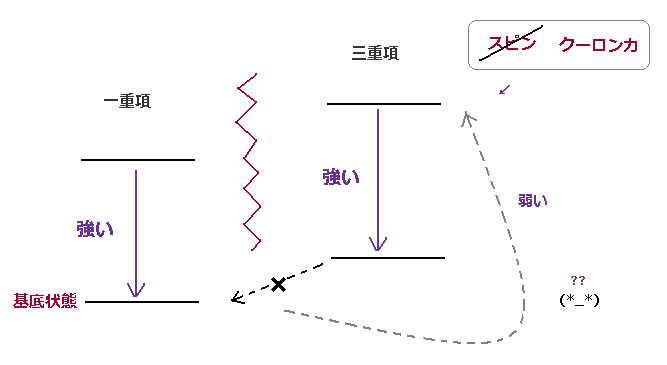
このサイト (p.5) や このサイト (p.3) に指摘されているように、 "一重項" と "三重項" のエネルギー準位差は 非常に弱いスピン磁気モーメントではなく、 クーロン力 によるものである。
非常に便利なことに、 選択規則というものがあって、この一重項と三重項の間の遷移が 禁止されているのである。 このサイト や このサイト (p.2) など参照のこと。
なぜなら もしこれらの準位がリアルなものだとしたら、遷移スペクトル線の数が 今よりも はるかに多くならないと 辻褄が合わないからである。
しかし 基本的な疑問として、 もしこの遷移が 禁止されているとすると、電子は 果たして どのように 一重項の基底状態から 三重項の励起状態に 上がる ことができるのか と思われる。矛盾以外何者でもない。
彼らが言うのは この遷移間の光は りん光 といって、非常に弱く観測しづらく、また 遷移時間が非常に長い としている。
このサイト や
このサイト 参照のこと。
しかし 非常にゆっくりとした 光の遷移供給 ( 基底状態 → 三重項 ) では、強力な (= 速い ) 三重項 - 三重項の遷移を説明することは できない。
Nist のデータ ( He, Mg ) では "term" の欄にあるように、一重項-一重項、 三重項-三重項 間の遷移のみしか見られないことになっている。
また 光子のスピン1の制約によって、特定の遷移 ( S-P、P-D 間 ) のみが許されるとしている。
この便利な選択規則というのは 様々な遷移における辻褄合わせのために 導入されたことは 一一目瞭然である。
実際に 副作用として Mg と Al+イオン のスペクトル線を比較すると、この両者は 同じ電子構造であるにも関わらず、 3p2 (= 三重項 ) の準位が 完全に 異なっている。
(Ap.1) 球と球殻における スピン速度。
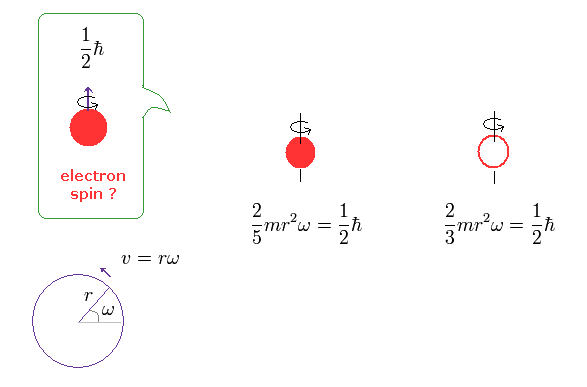
角運動量 L は 慣性モーメント × 角振動数 ω で表される。
Ap.1 の左図は 剛体球で、 Ap.1 右は 薄い球殻 である。 このサイト参照のこと。
最初に 剛体球の表面上の スピン速度 (= rω ) について計算する。
( 薄い球殻では 剛体球の速度の 3/5 倍にすればいい。 )
Ap.1 左にあるように、球面上の回転速度 (= rω ) は 光速を はるかに 越えてしまう。
(Ap.2)

ここで m は 電子質量、 ħ は h/2π ( h = プランク定数 ) である。
このスピン速度は 光速の 100 倍以上 (= 100 × c = 100 × 3.0 × 108 (m/s) ) にも達してしまう。
ここでは 電子の半径 (r) を 陽子半径 (= 0.88 × 10-15 m ) と同じくらいと仮定した。
しかし 実際の電子の大きさは 陽子よりも はるかに小さい。
Ap.2 を見て分かるように、 半径が小さくなるにつれて、その回転速度は 速くなる。
つまり 電子のスピン速度は 光速よりも はるかに速くなってしまう。 もちろん、こんなことはあり得ない。
(Ap.3) ↓ これは実験で確認されたのか ?
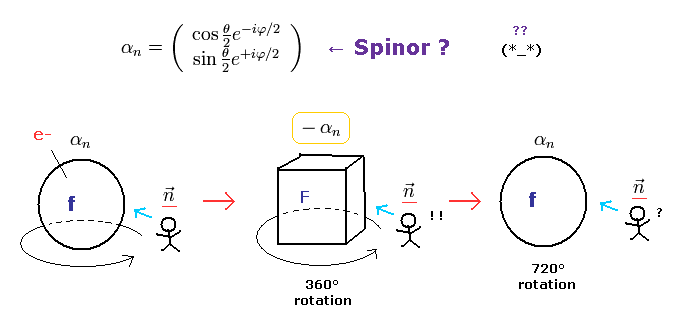
この奇妙なスピノルの性質は 実際の実験で確認されたと言われている ( [4], [5] )。
しかし 本当にそうだろうか?
これらの実験は フェルミ粒子を 中性子として用いている。
そして 中性子を 360o 回転させても 元に戻らなかったことになっている。
(Ap.4) 1つの中性子を回転させ もう1つはそのまま。 → 最後に 干渉させる。
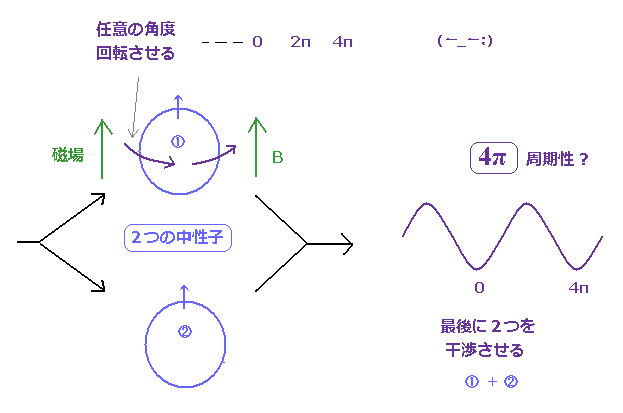
これらの実験では 同じ位相を持つ中性子を 2つの経路に分離させている。
そのうち1つを ラーモア歳差運動によって 磁場の下で 任意の角度 回転させる。
もう片方の中性子は そのままにしておく。
最後に これらの中性子を混合して 互いに干渉させる。
この実験では 中性子が 1回転で 元に戻れなかったとしている。 ( 2回転で戻った! )
(Ap.5) 磁気モーメント (= 中性子 ) に働くトルク。
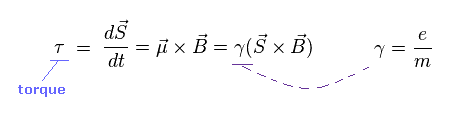
中性子は 中性電荷だが、弱い磁気モーメントを持つ。 ラーモア歳差運動によれば、外磁場 (= B ) の下で 磁気モーメント (= μ ) に対して 回転トルク が発生する。
"S" は 中性子の角運動量である ( この場合、 S = 1/2ħ )。
γ は 磁気回転比で、 μ と S との間の定数である。
(Ap.6) 電子の磁気モーメント = ボーア磁子。
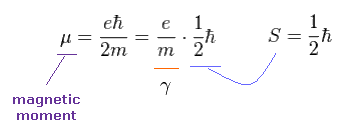
ここではまず 簡単に 電子の磁気モーメント (= ボーア磁子 ) を 使用して 計算してみる。
Ap.6 にあるように、スピン角運動量 S が 1/2ħ のとき、磁気回転比 γ は "e/m" になる。
ここでは 磁場 B は z 方向である。
外積の定義より、 Ap.5 は 次のように表せる。
(Ap.7) 磁場 B の下での ラーモア歳差運動。

Ap.7 から、歳差運動の角振動数 ω を得ることができる。
(Ap.8)
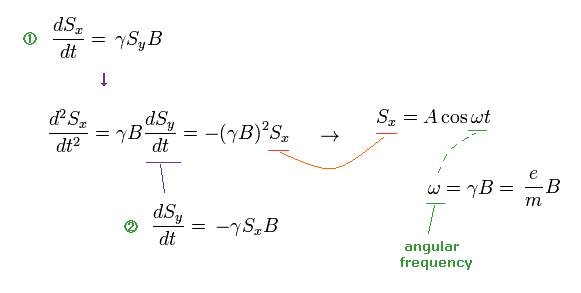
Ap.8 の ω の仮定に基づいて、彼らは 中性子の回転角度を 推定した。
つまり この前提となる仮定が異なると、回転角度も 異なることになる ( ← ここが重要。 )
もし スピン 1/2ħ の代わりに、ボーア軌道の通常の角運動量 (= ħ ) を用いると、磁気回転比は 次のように 半分になる。
(Ap.9)
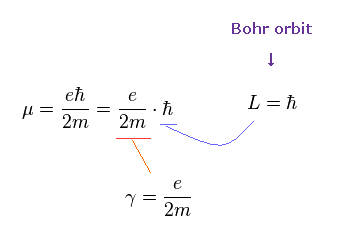
もし γ が 半分になると、角振動数 ω も 半分になる。
(Ap.10) スピンの代わりに ボーア軌道を仮定すると・・
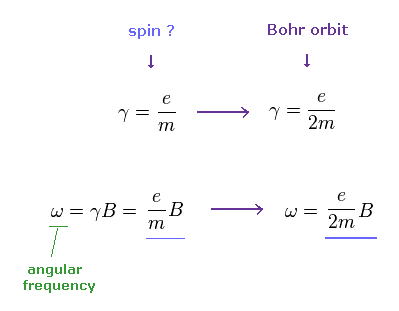
Ap.10 より、ボーア軌道 (= ħ ) を仮定すると、歳差運動回転角は スピンのケースの 半分 (= 1/2ħ ) になる。
つまり、この実験は 中性子が 1回転で 元に戻ったという 当たり前の結果を示しただけになる。
(Ap.11) ボーア軌道 vs. スピン。
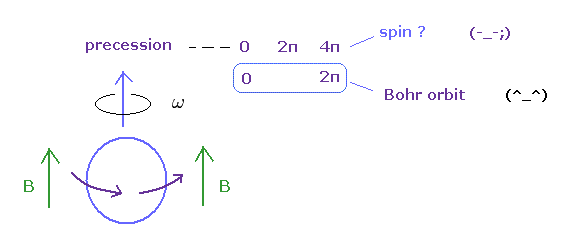
例えば、コマの歳差運動を考えてみると、角運動量が速くなるにつれて、その歳差運動速度は 遅くなる。
この現実の物が 360o 回転で元に戻ることを考えれば、ボーア軌道の角運動量が 正しく、 スピンが 幻想の産物であることが 容易に理解できる。
この "スピノル" の奇妙な性質は スピン角運動量 1/2 ħ から来たと言っていい。
もし 角運動量が ボーア模型のように ħ だと、波動関数は
(Ap.12)
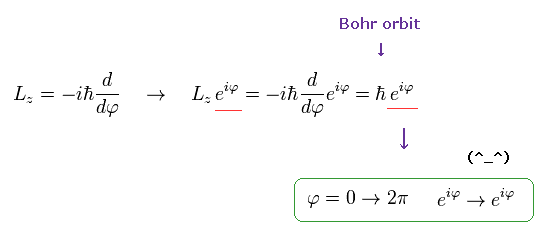
ここにあるように、この波動関数 ( eiφ) は 2π回転で元に戻る。
しかし もし角運動量が "スピノル"のように 1/2 ħ だと、波動関数は、
(Ap.13)
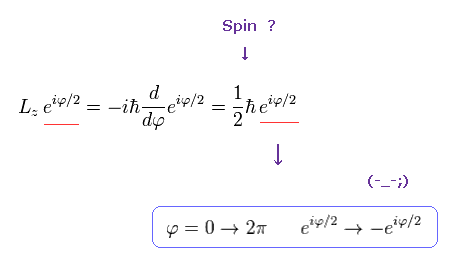
この波動関数 ( eiφ / 2 ) は 2π回転で 元に 戻らない。
つまり、本当の原子模型を考慮するときは、この 1/2 ħ という角運動量を忘れなければならない。
(Ap.14) 角運動量 = ħ → 1 × ドブロイ波長。
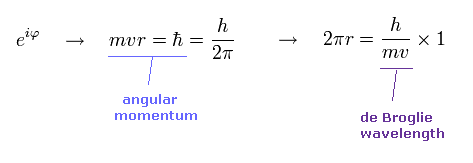
ボーア模型では、 最小の角運動量は ħ である。
Ap.14 にあるように、 角運動量が ħ のとき、その軌道長は ちょうど 1 × ドブロイ波長になる。
ドブロイの関係式は 全粒子で満たされる。
陽子や中性子では、スピン + ( 小 ) 回転が 複雑なg因子の原因と考えられる。
(Ap.15) 360o 回転で "スピノル" が 別の物に変化?

ここでは Ap.15 の奇妙な性質について説明する。
極座標を用いて 次の 単位ベクトルを定義する。
(Ap.16)

と パウリ行列 (= σ ) は、
(Ap.17)
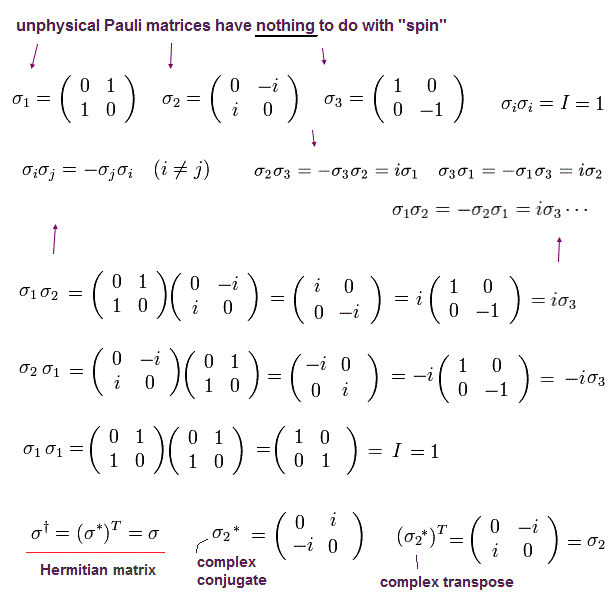
スピンが この単に行列の方向を向いているとき、スピン演算子 (= S ) は 次のように表せる。
(Ap.18)
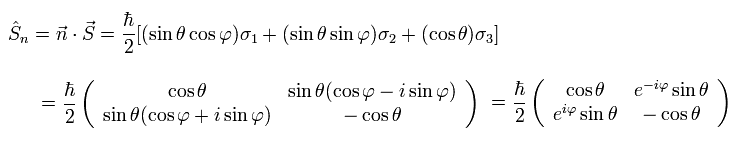
これは ベクトル n と S の内積である。
つまり n の方向を向いた "スピノル"を表す 固有関数は、
(Ap.19)

なぜなら、
(Ap.20)
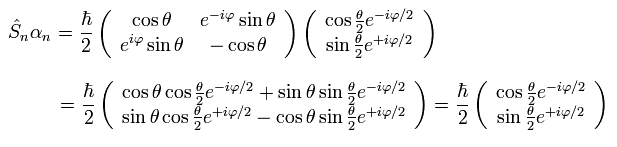
Ap.20 では、次を用いた。
(Ap.21)
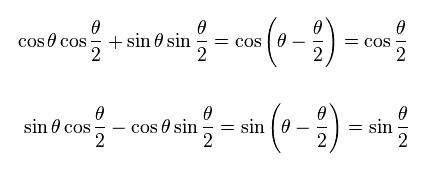
Ap.15 と Ap.19 のスピノルは 1回転で 元に 戻らない。
つまり スピノルそのものは 完全に 非現実的な概念ということになる。
異常ゼーマン効果 は ”電子スピン”が実際に存在することの証拠であるとされている。
しかし 1電子原子の水素原子は正常ゼーマン効果を示すことが知られている。
( また リチウム原子は パッシェン・バック効果で ナトリウムの D 線などよりもはるかに少ないスペクトル線しか観察されない。)
つまり 異常ゼーマン効果は”奇妙な”スピンよりもむしろ、内殻の電子によって生じると考えたほうが自然である。
弱い外磁場 (= z 方向 ) の下では、 ナトリウムの いくつかの線は 次のように ランデのg因子に従う。
(Ap.22)
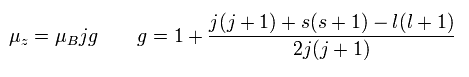
Ap.22 では、μz は、全磁気モーメント (μ) のz軸成分、μB はボーア磁子。
j (= ± 1/2, ± 3/2 ...) は、全角運動量のz成分、gはランデのg因子、s と l はそれぞれ、スピンと軌道角運動量のz成分である。
このランデのg因子 (g) はどうやって導かれたのであろうか?
(Ap.23) ↓ 異常ゼーマン効果?
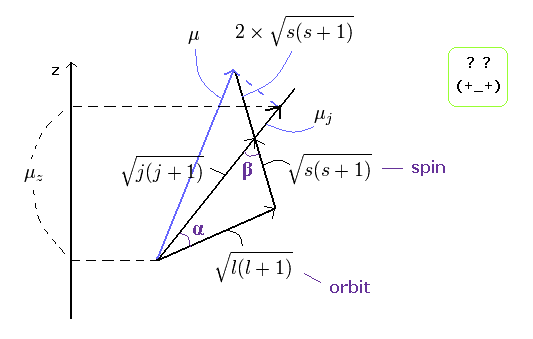
全 (j)、軌道 (l)、スピン (s) 角運動量は 上の "三角" の関係を満たす。
余弦定理より、
(Ap.24)
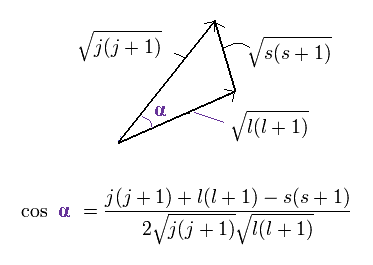
同様に、
(Ap.25)
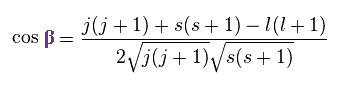
軌道 (l) と スピン (s) の 各磁気モーメントは、次のようになる。 ( スピンg因子 2 を用いて )、
(Ap.26)
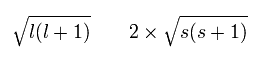
ここでは、 μj は 次の 全角運動量の方向を向いている。
(Ap.27)
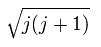
上記の軌道とスピンの磁気モーメントの μj 方向への 投影は、
(Ap.28)
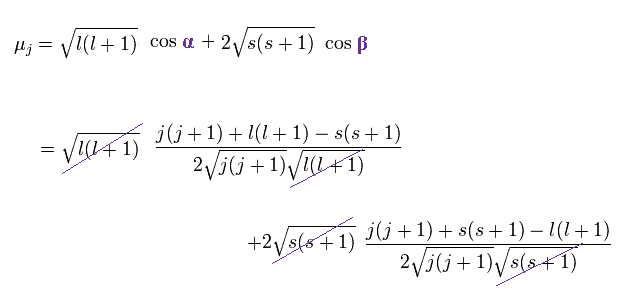
結果、
(Ap.29)
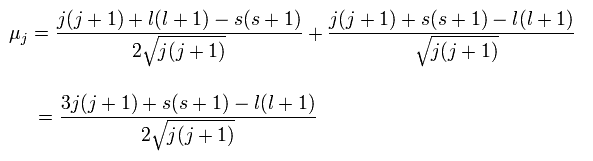
また この μj の z 軸方向への投影は、
(Ap.30)
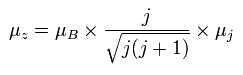
ここでは μB は ボーア磁子、 μz は 磁気モーメントの z 成分である。
Ap.29 を Ap.30 の μj に代入して、
(Ap.31)
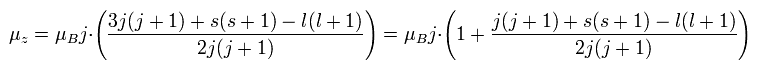
結果、Ap.22 のランデのg因子にたどり着けた。
これはつまり、弱い磁場の下では、 2つの 奇妙な歳差運動が 起きていることになる ( Ap.32 参照のこと )。
歳差運動 (1) ---- 全磁気モーメント μ が、全角運動量の方向 (すなわち μj の方向 ) の周りを歳差運動している。
歳差運動 (2) ---- この μj がさらにz軸の周りを歳差運動している。
(Ap.32) 異常ゼーマン効果における 2つの不自然な歳差運動。
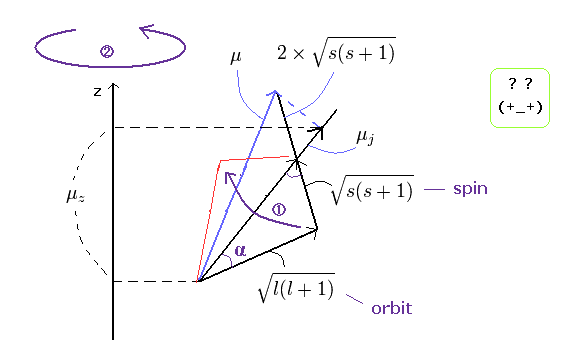
つまり、異常ゼーマン効果とは、非常にこみいったものなのである。
ここで、この1と2の歳差運動を注意深く見てみると、何か”奇妙な”ことに気づかないだろうか?
一般的に、物体は、磁場や重力といった何かの力の方向の周りを歳差運動するものである。
しかし、全角運動量 ( = μj の方向) は力の方向とは何の関係もない。
(図に示したように、 μj の方向は、外磁場であるz軸方向でもなく、また全磁気モーメント μ の方向でもない。)
また、この計算順序を見ればわかると思うが、歳差運動 (1) は、歳差運動 (2) よりもかなり速く回転していることが必要である。
つまり、歳差運動 (1) は非常に不自然なものなので、おそらくこれは起こらないであろう。
この歳差運動 (1) というのは、ナトリウムのスペクトラムのいくつか (例えば D線)を説明するために強引に作られたものなのだ。
また、ご存じのとおり、例えば、軌道 とスピン 角運動量のz成分、 l と s が、それぞれ 1 と 1/2 のとき、全角運動量のz成分 j は j = 1 + 1/2 = 3/2 になる。これは、この弱い磁場でもあてはまる。
しかし、この歳差運動 (1) によれば、スピン (もしくは、軌道) 角運動量のz成分は,時間とともに変動しており、例えば s は 1/2 以外の状態もあり得るとしている。
つまり、s = 1/2 + 0.05, l = 1 - 0.05, という場合もあり得るというのだ。
しかし、それらの合計した j は 常に 3/2 をとらなければならない。
( よって j = 1/2 + 0.05 + 1 - 0.05 = 3/2 ということになる。)
何か、矛盾してないだろうか? そもそも、j = 3/2 という条件は s (スピン) =1/2, l (軌道) =1 という前提条件に由来している。
しかし、ランデの理論は、この前提条件を後で無視してしまい、でも j = 3/2 だけは必ず順守しなければならないとしているのだ。
つまり、ランデのg因子 は 非常に不自然なものなのである。
電子スピン共鳴 (ESR) や 核磁気共鳴 (NMR) は スピンのラーモア歳差運動が関係していると言われている。
しかし、上で述べたように スピンそのものは現実の物で表現することはできない。
これは、スピンのラーモア歳差運動は単なる幻想だという意味であろうか?
Ap.5 と Ap.10 で示したように、磁場 (B) のもとでの 電子スピンの歳差運動の角振動数は次のようになる。
(Ap.33)
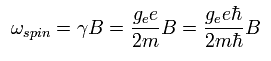
ここで ge は 電子スピンのg因子 で、ほぼ 2 である。 また B は 磁場である。
電子のボーア磁子は、
(Ap.34)
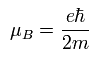
ESR や NMR の共鳴条件では、吸収(もしくは 放出) される電磁波が次のような スピンアップ ( S = +1/2 ) と スピンダウン ( S = -1/2 ) の状態間の エネルギー差 に等しいとしている。
(Ap.35) 吸収もしくは放出される電磁波のエネルギー。
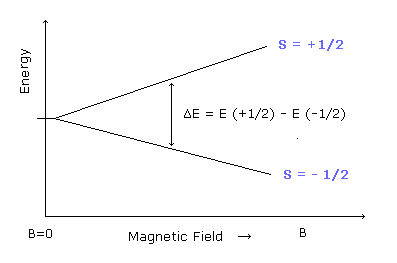
これらの2つの状態間のエネルギー差は次のように表される。
(Ap.36)
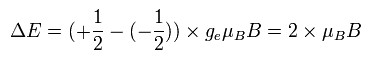
上で述べたように ボーア磁子は、ボーア模型と電子スピンに 共通の値である。
そのため、もし 奇妙なスピンの代わりに、ボーア模型を用いたとしたら、エネルギー差は次のようになる。(角運動量 ± 1)
(Ap.37)
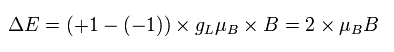
ここで gL は 軌道 g 因子で (ほぼ 1) であり、これは次の関係式を満たす。
(Ap.38)
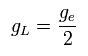
結果として、Ap.36 は Ap.37 に等しくなる。つまり、ボーア模型を用いたとしても EPR と NMR の現象を説明することが可能である。
これは、2 × 1/2 = 1 × 1 (= ボーア磁子 ) の等式が成り立っているからである。
量子力学の物理学者達は、スピンのラーモア歳差運動を使って、EPR, NMR の共鳴を 説明しようとしている。
これは正しいのだろうか?
Ap.36 ( Ap.37 ) のエネルギー差は Ap.33 のスピン角振動数を用いて表現できる。
(Ap.39)
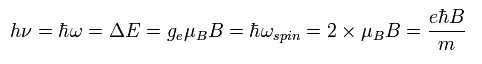
これが、物理学者達が スピンのラーモア歳差運動が 共鳴に関係していると主張している理由である。
しかし この解釈は”おかしな”ことを含んでいる。
上で述べたように、電子や中性子などのフェルミ粒子は 1回転で元に戻れない。(2回転でやっと戻る。)
つまり、2π でなく 4π の角度を 1周期の角度とすべきである。
すると、振動数 (角振動数でなく) は元の値の半分となってしまう。
これは、上記の解釈と矛盾していることになる。
ボーア模型では、電子は”スピン”のかわりに 回転運動している。
磁場 (B) のもとでは、ローレンツ力 は 次に示す角振動数の回転運動を生じさせる。
(AP.40)
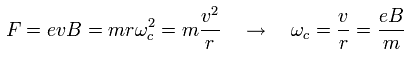
結果、共鳴エネルギーは次のようになる。
(Ap.41)
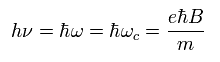
Ap.41 は AP.39 に等しい。
すなわち、”奇妙な”スピンの代わりに、普通の回転運動によって 共鳴が生じると考えたほうが しごく自然である。
ボーア磁子は ”理想的な”値である。
もし、1つの電子が一様に円軌道上に分割されて分布しているとしたら、電流密度は均等になり、ボーア磁子の値が正しいことになる。
しかし、1つの電子は 現実には 分割することはできない。つまり 軌道のg因子は 1 と少し異なることになる。
Eq.24 の ボーア磁子は ボーア・ゾンマーフェルト模型においては、いろんな エネルギー準位 ( n = 1, 2, 3...) の軌道に含まれる。
例えば、n = 3 の軌道には、角運動量が L = 1, 2, 3 の 3 パターンが存在するが、このうち L = 1 のとき、この軌道はボーア磁子の磁気モーメントを生じることになる。
なぜなら、磁気モーメント = g因子 (1) × L (1) × ボーア磁子 で表されるからである。
ちなみに n = 3 の準位では L = 1 の軌道は "楕円形" になる。
[1] G.E. Uhlenbeck and S.A. Goudsmit, Nature 117,264 (1926).
[2] 朝永振一郎、「スピンはめぐる」 (2008)
[3] J.C. Wesley and A. Rich, Phys. Rev. A4 1341-1363 (1971).
[4] H. Rauch et al., Phys. Lett. 54A, 425 (1975).
[5] S.A. Werner et al., Phys.Rev.Lett., 35 1053 (1975)

2014/5/12 updated This site is link free.