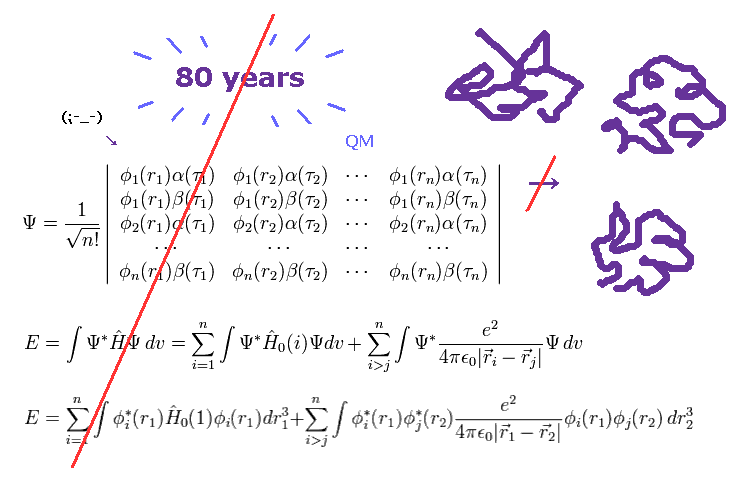
Top page (correct Bohr model including the two-electron atoms)
Strange "spin" is NOT a real thing
Manual of protein rotations and manipulations.
Protein-atoms collisions. (13/10/16)
(Fig.1) More than 80 years have passed. → quantum mechanics cannot do anything.
As I said, solving multi-electron wavefunction ( Schrodinger equation ) is too difficult to be applied to computing protein interactions.
To compute macro molecules using Schrodinger equation, we have to choose "artificially" some finite basis set.
Of course, small basis set cannot get correct energy state, and various different errors happen in each different basis set.
Bond energies such as hydrogen bonds and van der Waals force, which determine actual protein interaction, are less than one-tenth of covalent bond.
For example, total ionization energies of single oxygen ( 1-6th ) is 433.11 eV, which is much bigger than covalent bond (= about 3.0 eV ) and hydrogen bond (= about 0.1 eV ).
So total errors of the whole protein due to different choice of basis set is much bigger than these small bond energies.
(Fig.2) Rotations are blocked in both directions.
The whole protein structure can be determined by dihedral (= torsion ) angles.
At each rotational sites, amino acids can be freely rotated to some degree (= rotation isomers. )
In these webpages, we show the collisions of two distant amino acids block these rotations and determine the whole protein structure.
So proteins act like rotating solid body.
Here we use the following sample JAVA program to investigate and manipulate protein structures.
About the operation manual, see also this page.
Sample JAVA program ( PDB protein - rotation ).
First, we deal with following myoglobin.
Oxymyoglobin text ( 1MBO.txt ).
And this program can change each amino acid side chain ( for example, ALA → PHE ).
So we use the following text file as templates for 19 kinds of amino acids
19 amino acid templates ( tout.txt ).
(Fig.3) Change location folder.

Save this text at the location of "C:\sdff" folder as the filename of "1MBO.txt".
( Or you can save this protein text directly from PDB webpage. )
In the same way, save "tout.txt" in a folder, too.
( When you save in a different folder, change Fig.3 part inside program. )
After it, save the above sample JAVA program as "amic.java", and compile it.
You can run the program, as it is, neglecting notes such as "Recompile with -Xlint: unchecked for details ".
(Fig.4) Rotate all angles → Command prompt screen.
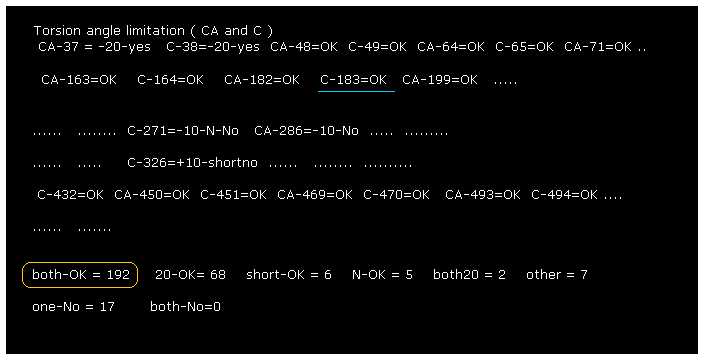
After running the program, if you input "0" (= Rotate all angles, yes ), the result of Fig.4 is displayed.
"C-183" means ( dihedral angle ) rotation at ( program ) atomic number "183" (= C, carbon ).
"both-OK" means the both-directional (= ±10 degree ) rotations are blocked, which means most stable.
( See also this page. )
This result shows our methods are one of crucial factors to determine actual protein structure.
We explain the meaning of Fig.4, taking "C-183" as an example.
(Fig.5) Selecting carbon-183.
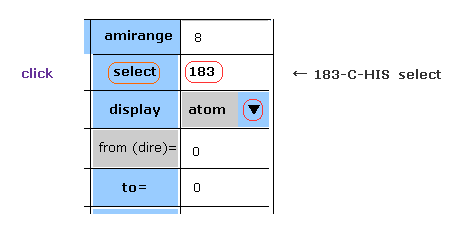
Choose "atom" in the scroll bar, input "183" (= program atomic number ) into textbox next to "select", and click "select" button.
If so, carbon atom of 183 becomes at the center on the screen.
(Fig.6) Narrowing y and z width.
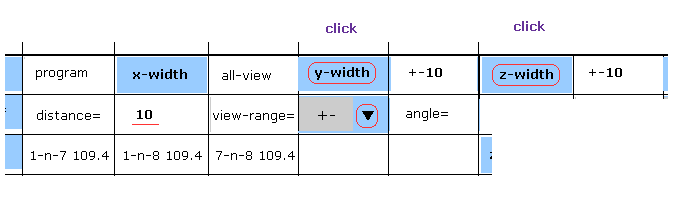
On the screen, all atoms of myoglobin are displayed, so it is difficult to grasp their relations.
So we narrow regions displayed on the screen.
Choose "+-" in the scroll bar, input "10" into the textbox next to "distance=".
And then click "y-width" and "z-width" buttons.
(Fig.7) Protein picture.

The designated atom is displayed as yellow square (= carbon-183 ).
For example, on x-z plane, only region within ±5 Å in the y direction is shown.
You can move or rotate the whole protein by clicking each triangle or circles on the edge.
(Fig.8) Dihedral ( torsion ) angle.

Dihedral ( torsion ) angle is a very important concept, because you can construct protein 3D structure only from the informations about all dihedral angles.
Dihedral angle means the angle between plane A (= 181-182-183 ) and plane B ( 182-183-198 ) in Fig.8.
When you input "183" into the textbox next to "from (dire)=" ( after choosing "atom" in scroll-bar ) , and click "dihedral" button, you can get dihedral angle of this ( between 182 and 183 ).
Here designate program number when "atom" condition, and PDB atomic number when "PDBat" condition.
(Fig.9) Choosing residue + "C".
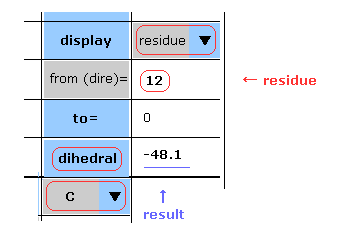
You can get dihedral hangles after choosing ( N, CA, C, CB, CG, ... ) and "residue" in each scroll bar.
In this case, choose "C", input PDB residue number (= HIS-12 ) into textbox, and click "dihedral" button.
( Basically, peptide bond is double-bond like, so in "N" case, this angle is about -180 degree. )
You need to be careful that hydrogens and oxygens are NOT involed in this dihedral angle at all.
(Fig.10) Dihedral angle and choice of atoms.
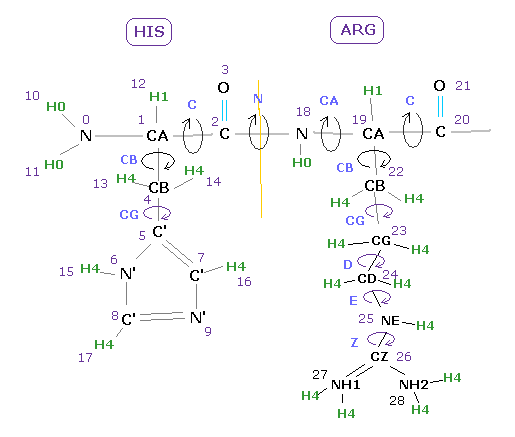
For example, if you want know the angle between 18-19 (= before CA ) in Fig.10, input atomic number of "19" into textbox, and click "dihedral" button.
Basically the angles just before CA and C carbons are refered as Ramachandran plot, which is very important for alpha helix and beta sheet structure.
If you input "4" (=CB ), you will know the angle between plane 0-1-4 and plane 1-4-5 in Fig.10 case.
If you input "26" (=CZ ), you will know the angle between plane 24-25-26 and plane 25-26-27.
( Of course, when you choose "residue" and "Z" in each scroll bar, and input residue number, you can get "CZ" dihedral angle. )
(Fig.11) Dihedral angle and atomic positions

As shown in Fig.11, when the atoms of 29 and 46 are arranged at "cis" positions, dihedral angles becomes "0" degree.
On the other hand, when they are at "trans" positions, the dihedral angle becomes -180 (or 180 ) degree.
From the viewpoint of Fig.11 (= arrow 30 → 31 ), vector 31-46 turns counterclockwise some angle ( for example 30 degree ), the dihedral angle becomes negative ( -30 degree ).
On the other hand, when it turns clockwise, its angle becomes positive.
(Fig.12) Distances between atoms on either side of C-183.
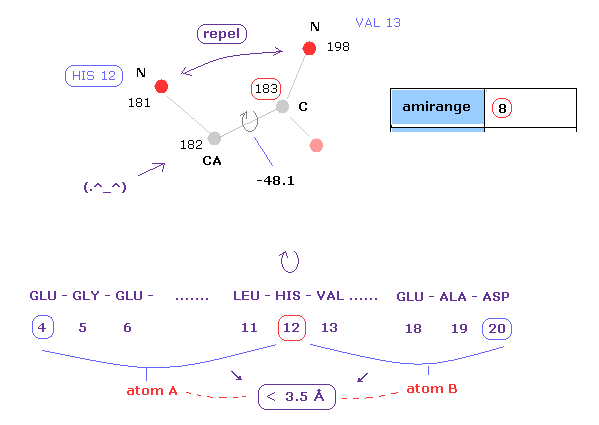
The important point is what determine each dihedral angle.
We pay attention to repulsive relations between atoms ( A and B ) on either side of designated dihedral angle.
When you click dihedral angle, after inputting "8" into the textbox next to "amirange", this program computes all distances ( excluding hydrogen ) between residue "4" (= 12 - 8 ) and residue "20" (= 12+8).
Here, atom A is inside residues from 4 to 12, another atom B is inside residue from 12 to 20.
Carbon atoms 182 (=CA ) and 183 (= C ) don't influence this dihedral angle at all.
( For example, the distance between 182 and 198 doesn't change by rotating this dihedral angle. )
In these cases, atoms 182 and 183 are excluded from this calculation.
(Fig.13) Distances less than 3.5 Å between two atoms on either side of 182-183.

This program display only interatomic distances less than 3.5 Å excluding hydrogen on command prompt screen.
As shown in this page, hydrogen atom has very week repulsive effects, so we neglect its effects here.
In Fig.13, for example, the distance between oxygen atom (= program number 130 ) and nitrogen (= 198 ) is 3.364 Å.
The shortest distance, which influences this dihedral angle is 2.765 Å, which is between nitrogens 181 and 198 of Fig.12.
The important point is that almost all distances are more than 2.8-2.9 Å due to steric hindrance.
( This is very important factor in determining protein structure. )
(Fig.14) Rotation of all amino acids after C-183 by 10 degree.
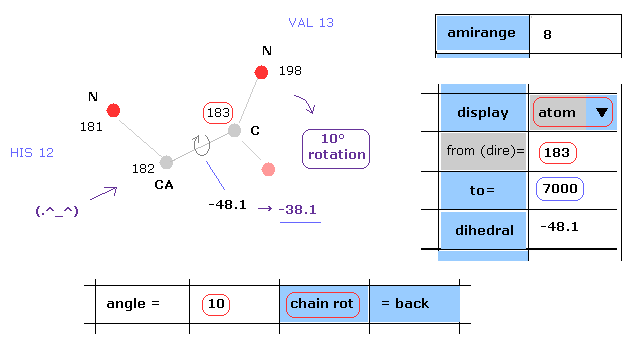
Next we rotate all amino acid chains after carbon-183 by 10 degree.
Input "183" and "7000" into textboxes next to "from(dire)=" and "to=".
( The last atom of myoglobin is 2843, so this "7000" can be changed into arbitrary number above 2843. )
And input "10" into the textbox next to "angle=", and click "chain rot" button.
This myoglobin includes 2843 atoms, so in this case, all atoms after carbon-183 are rotated around the axis of 182-183 atoms by 10 degree.
( So dihedral angle changes from -48.1 to -38.1 degree. )
(Fig.15) Rotation of all amino acids after C-183 by 10 degree - residue.
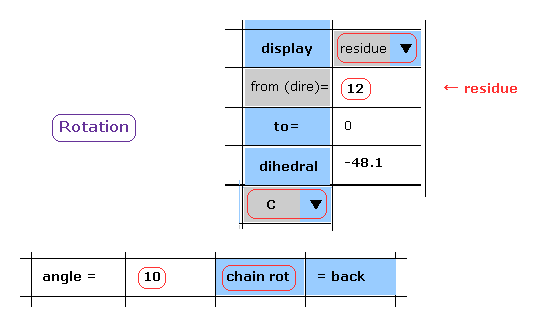
When you chooce "residue" and "C" in each scroll bar, you can rotate like Fig.14.
After input "10" (= rotation angle ) and "12" (= residue number at rotation site ) into each textbox, and click "chain rot" button.
In this case, irrespective of the value next to "to" button, all amino acids after C-183 are rotated by 10 degree.
(Fig.16) Interatomic distance change after rotation.

On the command prompt screen, interatomic distances, which become shorter than before rotation, are displayed.
As shown in Fig.16, the distance between nitrogens 181 and 198 becomes too short ( 2.765 Å → 2.690 Å ).
This site exerts strong repulsive effect, and blocks this rotaion by steric hindrance.
Shortest length before rotation is 2.764 Å, as shown in Fig.13.
So this shortest length becomes much shorter by this rotation.
(Fig.16') Shortest interatomic distance becomes much shorter → this rotation is blocked.

Also on the protein screen we find the interatomic distance between nitrogens 181 and 198 becomes shorter.
As a result, the shortest interatomic length becomes shorter after this +10 rotation.
It means this rotation is blocked by steric hindrance.
(Fig.17) Rotation back → rotation by -10 degree.
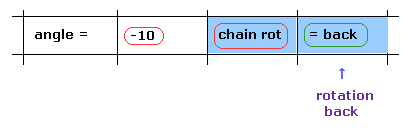
Next we investigate rotation in the opposite direction.
Click "=back" button to the original configuration.
Then input "-10" to the textbox and click "chain rot" button.
In this case, all amino acids after carbon-183 are rotated by -10 degree.
( As shown in Fig.11, positive angle is clockwise, negative angle is counterclockwise. )
(Fig.18) Rotation by -10 degree.

As shown in Fig.18, also -10-degree rotation, some interatomic distance becomes too short.
The atomic distance between oxygen 149 and nitrogen 214 becomes 2.698 Å.
In this case, alpha helix of these regions becomes too tight by this rotation.
(Fig.18') Shortest interatomic distance becomes much shorter → this rotation is blocked, too.
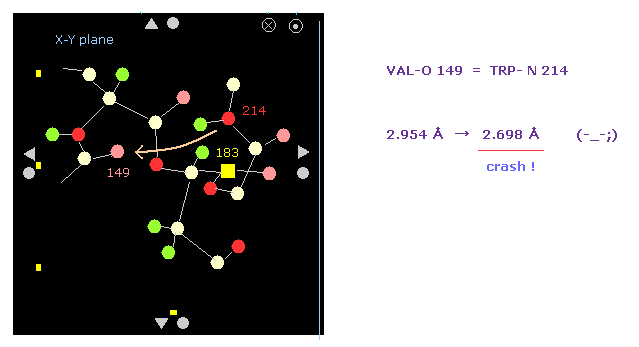
Also on the protein screen we find the interatomic distance between O-149 and N-214 becomes shorter.
As a result, the shortest interatomic length becomes shorter also after this -10 rotation.
It means this rotation is blocked by steric hindrance, too.
So the dihedral angle of of -48.1 degree is the most stable state (= avoiding all obstacles ).
This means one or two conspicuous obstacles are key players to determine each dihedral angle.
(Fig.19) Most stable dihedral angle.
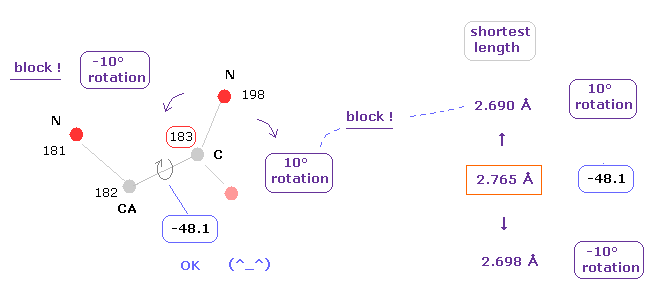
The key point is the shortest interatomic distance.
Because even if there are only a few unreasonably short interatomic length, this rotation can be blocked.
So the present protein structure is the result of avoiding any single obstacle.
This is a true reason to determine protein struture.
(Fig.20) Almost all dihedral angles are fixed.

After running the program, if you input "0" (= Rotate all angles, yes ), the result of Fig.20 is displayed.
"CA-37" means rotations at program atomic number "37" (= CA ).
"both-OK" means the both-directional (= ±10 degree ) rotations are blocked like Fig.19, which means most stable.
"20-OK (yes)" means rotation in one-direction is blocked by +10 degree, and another direction is blocked by -20 degree.
So also in this case, both-directional rotations are almost blocked and stable.
"one-No" means one-directional rotation is blocked, but another-directional rotation is not blocked.
These sites are near surface of the protein, which rotation is probably blocked by other proteins or something.
The total number of both-blocked C, CA sites in myoglobin is 192, which is much bigger than 17 (= one is not blocked ).
This result shows even one or two obstacles (= shortest interatomic length ) are very important key factor to determine each dihedral angle.
(Fig.21) Rotations are blocked in both directions.

The whole protein structure can be determined by dihedral (= torsion ) angles.
At each rotational sites, amino acids can be freely rotated to some degree (= rotation isomers. )
As shown in this page, we show the collisions of two distant amono acids block these rotations and determine the whole protein structure.
So proteins act like rotating solid body.
(Fig.22) Rotation at C sites.

In C sites, the repulsive force between two nitrogens near C is very important.
+10 rotation makes this distance much shorter, so it is blocked.
-10 rotation makes this distance longer, but instead other atoms come too close to each other and blocked.
The calculation of this program considers only the shortest interatomic length.
In some cases, the original N-N length remains shortest after -10 rotation.
In these cases, if rotation is blocked except only for this N-N length, this case is displayed as -10-N-No.
And in some sites, we rarely see unnaturally short atomic length ( about 2.650 Å ) even in the original form.
Even when some rotations are not blocked, if they are blocked by excluding only this unnatural short length, words such as "+10-shortno" are displayed.
Try rotating these sites and confirm them ( program atomic number is displayed. )
(Fig.23) Changing amino acids regions.

In the above section, we compute only ±8 amino acids regions, as shown in Fig.12.
But there are some amino acid parts which distances are very close to each other, though their residue numbers are apart from each other.
Change the value of "int searchrange=20" in the above program, and run it.
This variable means computing amino acid range.
When this value is 20, this program compute all interatomic distances within ±20 amino acids on either side.
( Or use the program below. )
Sample program ( ami2.java. computing range ±20 ).
(Fig.24) Rotations are almost all blocked (= both-OK ).
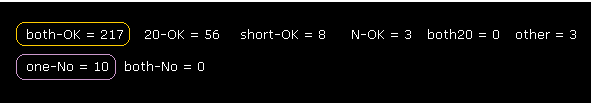
As shown in Fig.24, when we expand computing regions, we easily find that rotation of each dihedral angle is clearly blocked.
"both-OK" means rotations in both directions are blocked.
( In both ±10-degree rotations, the shortest interatomic length becomes much shorter = both rotation blocked. )
Total number of both rotation blocking sites is 217, which is much bigger than non-blocking sites (= only 10 ).
(Fig.25) Two distant amino acids crash.

Even when residue numbers are apart from each other, original interatomic distances may be short.
In these cases, by rotating some sites which are apart from them, two atoms may crash into each other, like Fig.25.
As a result, "192" of Fig.20 (= ±8 range ) is increased to "217" in Fig.24.
These results indicate protein's structure is like some solid body.
When only a part of these solid bodies crash into each other, this conformation change is inhibited.
Even a few very short interatomic distances play important roles to determine protein structure.
(Fig.26) Changing proteins.

Next we investigate calmodulin protein.
Save the above text file ( or directly from PDB website ) into a folder.
Change some parts inside the JAVA program like Fig.26, and recompile it.
( Transfer /* ---- */ from 1CLL to 1MBO. )
(Fig.27) Calmodulin rotating limitation results.

As shown in Fig.27, almost all chain rotations are blocked in both (= ±10 degree ) directions.
If you add 54 (= one direction is 10, another direction is 20 degree, blocked ) to 180, the total number of ( rotation ) blocked sites is "234".
This value of "234" is much bigger than non-blocked sites (= total number is "24" ).
This means calmodulin protein structure is determined by a few conspicuous obstacles within ±8 aminoacids from each one.
( This structure is similar to myoglobin, which contains many alpha helixes. )
(Fig.28) Changing amino acid "searchrange".

Next we change amino acid search-range from ±8 to ±20 and recompile it, like Fig.23.
( Make the variable "int searchrange = 20". )
In this case, we find the shortest interatomic distance within ±20 aminoacids from each rotation site.
(Fig.29) Calmodulin results ( ±20 range ).

As shown in Fig.29, when we increase search range from ±8 to ±20, we find rotations are more blocked.
This means in some parts, the collisions between distant amino acids determine their dihedral angles.
This is also an important result.
So the original stable conformation is the result of avoiding any conspicuous obstacles including near to distant atoms.
This result indicates proteins acts like some solid bodies.
As you see in Fig.20,24,27 and 29, in myoglobin and calmodulin, amino acids within ±8 range from each one are a key factor to determine almost all conformation.
Because these proteins include many stable alpha helixes.
PDB 2J96.txt ( protein dimer )
Next we investigate one of photosynthesis proteins (= PDB 2J96 ).
Save the above text file ( or directly from PDB website ) into a folder.
Change some parts inside the JAVA program like Fig.26, and recompile it.
(Fig.30) 2J96 rotation limitation results.

As shown in Fig.30, almost all chain rotations are blocked in both (= ±10 degree ) directions, like myoglobin and calmodulin cases.
2J96 is dimer. In this case, this program compute only subunit A.
And this computing don't consider collisions between subunit A and B, and protein and HETATM.
Of course, if we consider all these collisions, we find more rotation sites are blocked.
(Fig.31) Changing amino acid "searchrange" into "20".

Next we change amino acid serch-range from ±8 to ±20 and recompile it, like Fig.23.
Comparing Fig.30 and Fig.31, you find some sites are blocked by distant amino acids.
But almost all rotation sites are determined by amino acids included within ±8 from each one.
PDB 2PAH.txt ( hydroxylase dimer )
Next we investigate one of hydroxylase proteins (= PDB 2PAH ).
Save the above text file ( or directly from PDB website ) into a folder.
Change some parts inside the JAVA program like Fig.26, and recompile it.
(Fig.32) 2PAH rotation limitation results.

As shown in Fig.32, "290" rotation sites are blocked in both (= ±10 degree ) directions.
But in 2PAH hydroxylase, as much as 121 sites are not blocked.
So these kinds of enzymes are more flexible than myoglobin and calmodulin.
(Fig.33) Changing amino acid "searchrange" into "20".

Next we change amino acid search-range from ±8 to ±20 and recompile it, like Fig.23.
Comparing Fig.32 and Fig.33, you find much more rotation sites are blocked in Fig.33.
( "290" of Fig.32 is increased to "403" of Fig.33. ).
This result shows in 2PAH protein, more distant amino acids are key players to determine each dihedral angle.
Try the following proteins changing searchrange.
1ROP.txt ( transcription regulator )
1CTS.txt ( citrate synthase )
1TGH.txt ( transcription / DNA )
(Fig.34) What determine "hydrophobic (-philic) property ?

Basically, hydrophobic amino acids such as leucine and phenylalanine exist inside proteins.
And hydrophilic amino acids such as glutamic acids and asparagine are on the surface of the proteins, and confronting the water molecules.
One of the main reason is hydrogen bonds, they say.
But for example, why " C-H ---- O " cannot be hydrogen bondes ?
( Though " N-H ---- O " or " O-H ---- O " are common form of hydrogen bonds. )
Unfortunately, the present quantum mechanics cannot explain the true mechanism of this important property.
(Fig.35) All valence electrons of carbon cannot move (= bound state ).

Usually, when some positive charge approaching, some of valence electrons try to move a little toward this positive charge, and cancel this repulsive force.
But in case of carbon, all four valence electrons are already tightly bound to other nuclei, and cannot move.
( Except for the cases that positive charge is so big to break the covalent bonds. )
If one of C valence electrons moves toward oxygen, it means other positive nuclei moves in the opposite direction.
But the covalent bond is so tight that it's difficult for this phenomenon to happen.
(Fig.36) Free valence electrons of oxygen move toward other positive nuclei.

On the other hand, oxygen has six valence electrons and four electrons of them are free (= not bound ).
These free electrons are always finding other positive nuclei and try to move toward them.
So this movement cancels the repulsive force between nuclei out.
(Fig.37) Attracting power of "up" and "down" O electrons.

Basically attracting power of up and down valence electrons of oxygen is very strong.
As shown in Fig,37, when the force between electron and oxygen nucleus is "F", attracting force perpendicular to it is F sinθ.
The derivative of it with respect to θ is cosθ.
As shown in Fig.37, this derivative (= force increasing rate ) is biggest, when this θ is near zero.
When repulsive force of other nuclei become too strong, this θ becomes close to 90 degree.
In this case, force increasing rate becomes small comparing repulsive force between up and down electrons.
(Fig.38) Free "up" and "down" N electrons move toward other nuclei.

Also in nitrogen (= N ) atom, "up" and "down" electrons are free, and finding other positve charges.
So O-O and O-N length can be as short as 2.5 Å, while O-C length cannot.
( Excluding atoms near C linked by tight covalent bond. )
As I said in this page, when oxygen comes closer to hydrogen than this length, the repulsive force between O and H becomes stronger, and block it.
(Fig.39) Atoms around iron in myoglobin.

Using this PDB file ( 1MBO ) (= oxymyoglobin ), we find atoms around iron (= FE ) are always nitrogen or oxygen.
In Fig.39, select FE atom "1276" at "PDBat", click "center" button (= at the distance 7 Å ), and then make y-width ± 4.0 Å.
Nickel tetracarbonyl is one of organometallic compounds.
Different from usual compounds, this includes carbon - metal bonds.
( Of course, due to triple bonds, these compounds are unstable. )
(Fig.40) Nickel tetracarbonyl.
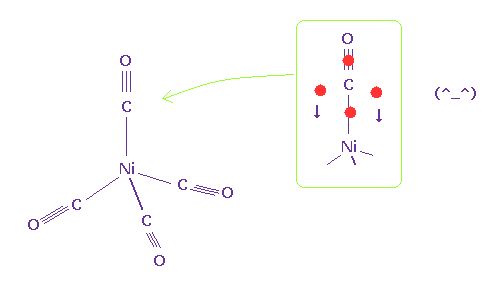
The important point is that this carbon atom does NOT form four single bond.
If four single bonds are formed like Fig.35, this carbon atom doesn't have the power to resist the strong positive force of nickel.
As shown in Fig.40, it is natural that excessive two valence electrons of carbon move to deal with repulsive force of nickel.
As shown in this page, triple bond doesn't mean all three electrons are packed into one single bond.
Because repulsive force among four valence electrons of carbon becomes too stronger.
(Fig.41) Carbon comes towards other C-H, avoiding oxygen.

Using this program, repulsive force between C-C is weaker than C-O.
So carbon atom (= C ) tries to avoid oxygen (= O ) of water, and come toward other C-H residue.
Fig.35 (= C valence electrons ) and Fig.41 are a true mechanism of hydrophobic property.
C-C length between subunit A and B proteins are about 4.0 Å.
So due to small repulsive force between C and C, they try not to come close to each other than this length.
In this C-C length, there is almost no space for H2O molecule to enter between C-C ( considering hydrogen atoms, too ).
This means hydrophobic parts of two proteins stick to each other by negative selection at the contact surface.
(Fig.42) N --- H - N (= nitrogen ) hydrogen bonds
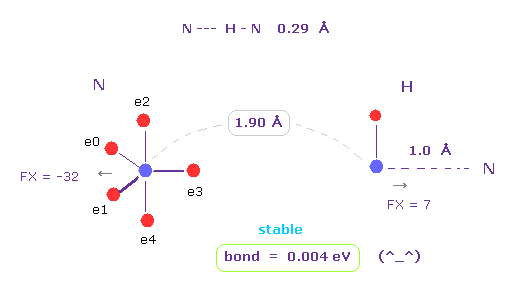
As shown in this page, hydrogen atom has very weak repulsive force.
And it includes only one negative electron and one positive nucleus.
So in some interatomic length, its bond energy tends to be positive and stable.
This property is specific only to hydrogen atom.
(Fig.43) When they choose steric hindrance or covalent bonds.
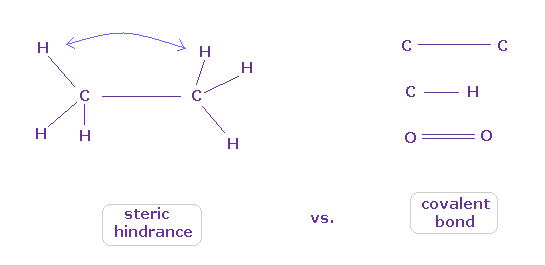
You often see the explanations such as " six hydrogen atoms of ethane tend to avoid each other." or "protein structures are very limited due to their steric hindrance".
So this means each atom "always" avoids other atoms ?
On the other hand, various atoms except for noble gases can form stable covalent bonds.
Though each atom "avoids" each other, why they can form stable and tight covalent bonds ??
In fact, these differences depend on their bond length.
(Fig.44) C-C = 1.5400 Å is an equilibrium length.
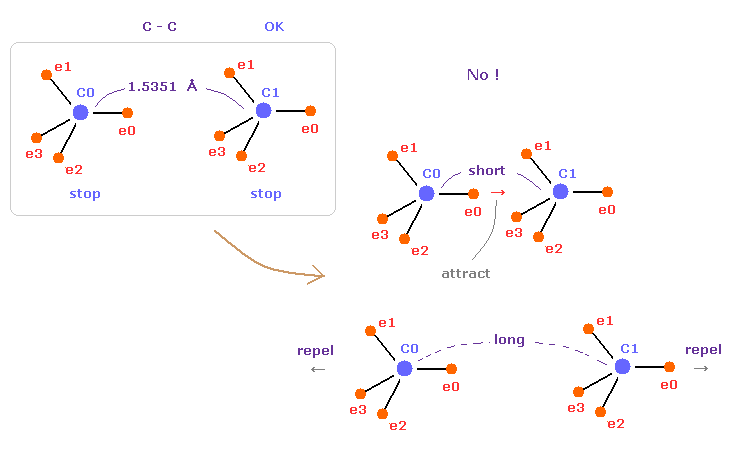
In this page, we show C-C bond length (= 1.5351 Å ) is indispensable for the stability of both C nuclei.
If C-C bond length is shorter than 1.5351 Å, attractive force between e0 and C1 becomes too stronger, and it's unstable (= binding energy becomes bigger. ).
And if C-C bond length is longer than this, repulsive force between two C nuclei becomes dominant, and it's unstable (= binding energy becomes negative ).
This latter case corresponds to, what we call, steric hindrance.
(Fig.45) "Long" or "short" bond length determines their property.
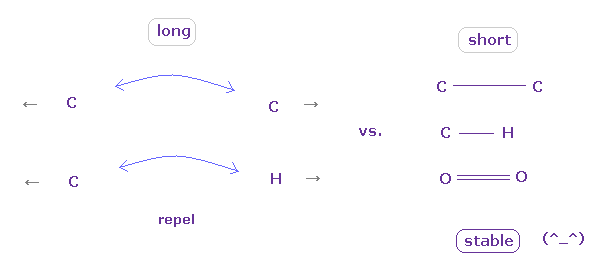
To form stable covalent bonds, two atoms need to come close to each other than some threshold length.
When it is longer than the threshold length, repulsive forces among electrons or nuclei become dominant and causes steric hindrance.
In usual proteins, almost all distances between two atoms are longer than covalent bond length, so they tend to cause steric hindrance.
(Fig.46) Rotations are blocked in both directions.

As I explain in this page, even when there are a few conspicuously short interatomic distances, this rotation is almost blocked.
Of course, this effect is caused by steric hindrance as shown in Fig.43-Fig.45.
As a result, while each carbon atom is trying to avoid oxygen ( of H2O ), two main factors of hydrogen bonds and rotation blocking determine protein structure.
(Fig.46) Amino acid construction.

This program can construct new amino acid chain.
Change the designated sites inside the program like Fig.26.
Sample JAVA program ( ami3.java protein construction ).
In Fig.46, change the variable like "int constr = 1".
"String sequence[]" mean amino acid chains we construct.
In Fig.46, 22 × leucines are constructed.
Change the variable "resn" to total number (= "22" ) of amino acids.
"CAang" and "Cang" mean the initial dihedral angles of all CA and C sites.
When CA and C dihedral angles are -60 and -50 degree, respectively, this protein becomes typical alpha helix.
(Fig.47) Hydrogen bonds in alpha helix (= total 22 amino acids ).
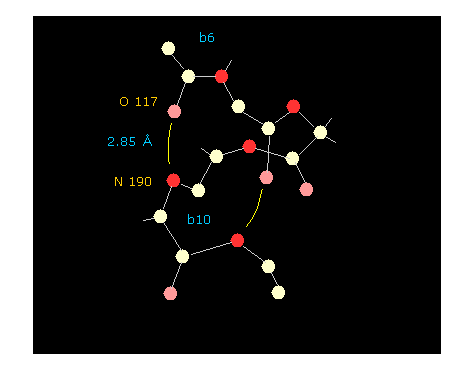
If you click "hydrogen" and "chain" buttons, you can display only main chain without hydrogens.
When you click some oxygen and nitrogen consequtively, interatomic distance between them is shown in the above textboxes.
As shown in Fig.47, oxygen of residue "6" and nitrogen of residue "10" form hydrogen bond, which length is as short as 2.85 Å.
If you change the whole dihedral angle ( using "Change-d" button, see this page ), you easily find how this hydrogen bond changes depending on dihedral angle. Try it.
(Fig.48) Chainging alanine into phenylalanine.
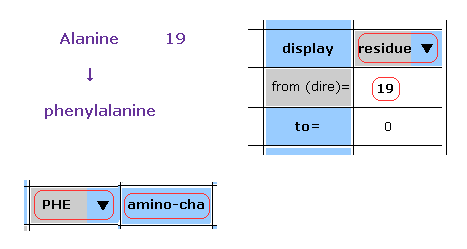
In this program, we can change the kind of each amino acid.
For example, residue 19 is alanine.
Choose "residue" in the scroll bar, input "19" into the textbox next to "from (dire)=".
And choose "PHE" in the scroll-bar ( seventh line ), and click "amino-cha" button.
(Fig.49) Alanine → Phenylalanine.
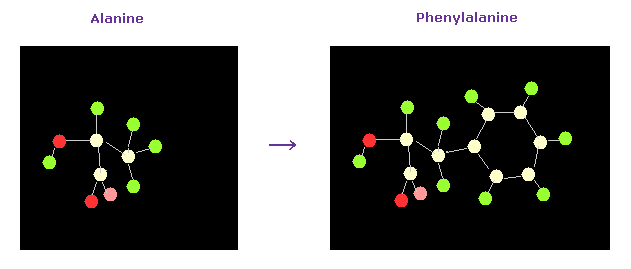
As a result, the designated amino acid is changed.

2013/8/29 updated. Feel free to link to this site.