Top page (correct Bohr model including the two-electron atoms)
Strange "spin" is NOT a real thing
Why they intentionally make physics difficult ?
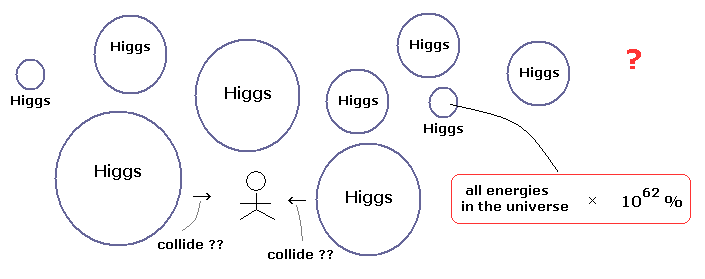
(Fig.1) "Infinite" heavy Higgs particles are really "flying" and giving mass to everything ??

We often hear the big news such as "Higgs particle has been found in the accelerator".
But now, we need to calmly think about this particle's reality and usefulness again.
As you know, "Science" is just equal to "asking what and why?", when there are something unknown in front of us.
And "Science" will be automatically useful for us someday, if it is "real".
As shown in this page, though they insist infinite Higgs particles are flying around us, they can find only one Higgs in more than trillions of collisions in the accelerator.
( Almost all of them are infinite noises ! )
Furthermore, they cannot observe Higgs directly, and just estimate its existence from final products such as lights.
(Fig.2) Fractional charges such as -1/3, +2/3 are real ?

We often see the comments such as quarks with -1/3 or +2/3 fractional charges have been actually found.
As you know, these explanations are exaggerations, and completely wrong.
Because fractional charges themselves have not been found, and they insist quarks and gluons can NEVER be isolated.
Indirect measurements of quarks in the accelerator are only a few things, almost all of them are infinite noises (= meaningless ), which is the same pattern as Higgs.
Actually, ONLY 20 top quarks, which is as heavy as gold atom, have been found ( not directly ) inside infinite noises until now, they insist.
Though these indirect measurements are all unclear and vague, why we must accept these imaginary particles as reality ?
(Fig.3) "Time gap" causes illusory particles.
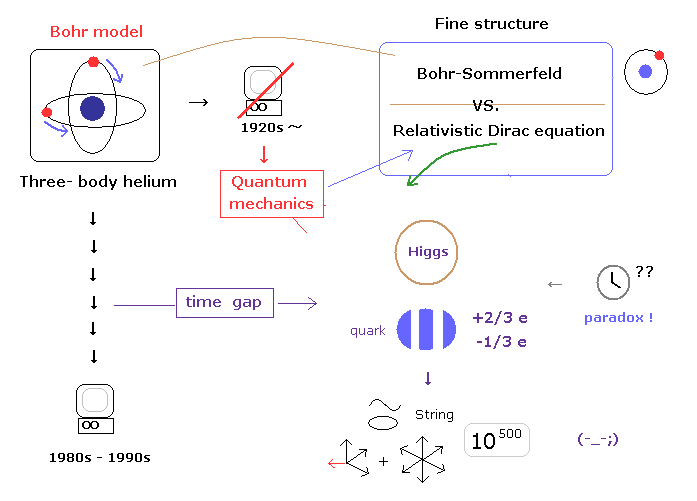
As shown in this page, these distorted situations were caused by "time gap" ( 1920s - 1990s ) related to complicated three-body helium and computers.
These are the same as the reason why unreal entanglement, quantum computer, black hole, and string theory need to be admitted.
Unfortunately, if you accept these fractional charges and Higgs as reality, there is only 10-dimentional string theory ( or 11-dimensional M theory ), which is left in front of you.
First, as shown in this page, if you neglect actual proof that special relativity is wrong, it is natural that various strange illusions like these happen.
(Fig.3') Results of "long" history = victory of "unreal" string theory.
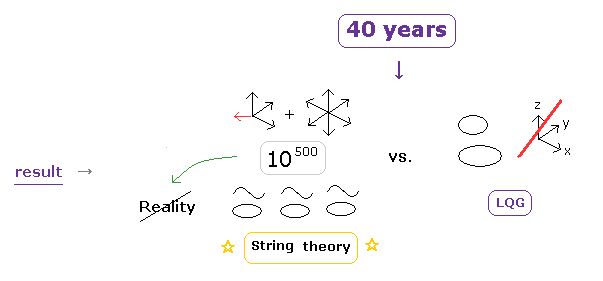
As shown in this page, other gravity theories such as loop quantum gravity (LQG) failed to unify quantum mechanics and relativity, so unreal string theory is the only final theory, and dominant in the present physical world, as you see.
If LQG can succeed as unifying theory, it would have already been successful long ago.
But it couldn't.
So plenty of time (= more than 40 years ) has passed to exclude other gravity theories such as LQG.
LQG changes 3-dimensional space into one-dimensional loop.
Personally, I think this drastic change of concepts about 3D → 1D space is a different kind of another dimension.
(Fig.4) No many worlds, No pilot wave → "Shut up !" forever = NOT science.
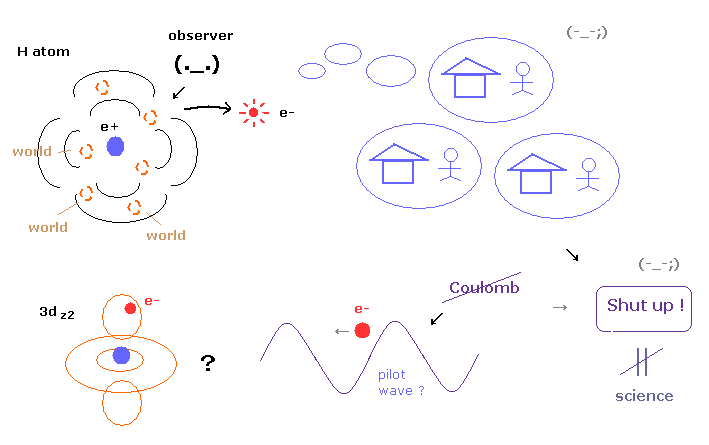
As shown in this page, many-world theory (= leading theory now ) is very unrealistic, and pilot wave theory does not use Coulomb force, and cannot explain the reasonable mechanism between pilot wave and particles.
All interpretations are very unnatural and have fatal defects, so almost all physicists do just "Shut up and calculate !", which means they give up asking what.
Actually arguments about interpretation of quantum mechanical wavefunction collapse is endless.
Even if we continue discussing this theme forever, there would be NO progress at all.
But "science" is to ask what or why, when there are something unknown in front of you.
So as you feel, giving up asking (= "Shut up and calculate !" ) is NOT science.
(Fig.5) When and why the present quantum mechanics becomes so strange ?
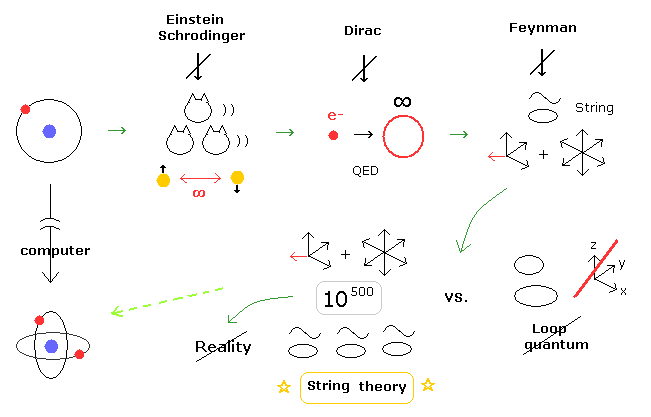
As you feel, many-worlds interpretation (= Schrodinger's cats ), faster-than-light entanglement, infinity of QED, fractional charge (= quarks ), 10-dimensional string theory are all unreasonable and unreal.
As shown in top page, all these serious problems are caused by very complicated three-body helium and lack of computers in 1920s.
Of course, going back to early physics of Bohr model would have very enormous influences on present physics.
( I understand they don't want to return as far as to this early physics due to these drastic influences and changes. )
But Bohr model is a very consistent and convincing reason why the unreasonable and unrealistic quantum mechanical worlds continue, left as it is, even now.
(Fig.6) These illuosory concepts are completely useless "forever".
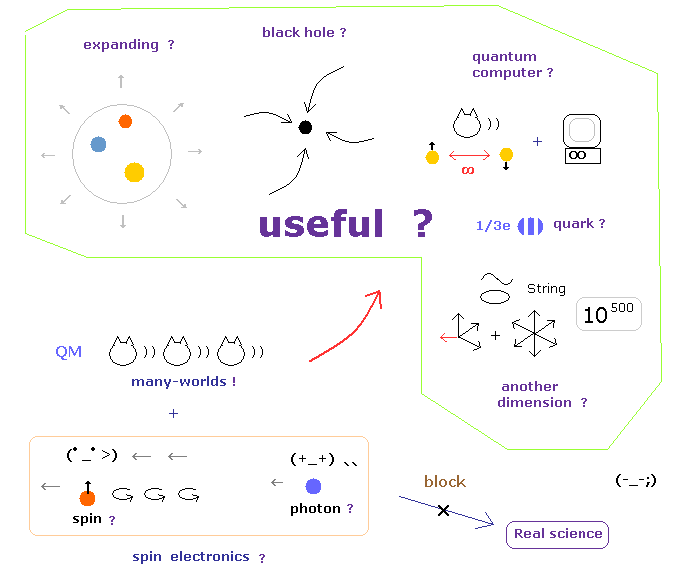
For example, when you hear the sensational news about Higgs finding, you need to ask yourselves whether these particles will be really useful for our daily livings.
When we ask about the difference between infinite Higgs paticles and aether, they just repeat Higgs particles are different from Higgs field and aether, and say just " Shut up !"
And if we try to utilize the phenomena inside infinite noises in the accelerator, unrealistic virtual particles, which violates relativity, obstructs it.
And the present researches and journals about spooky links and entanglement clearly consider unrealistic worlds as victory of physics, and are aiming at just unreality.
As you notice, aiming at unrealistic worlds means these would NEVER be useful for our daily livings, because they are unreal.
(Fig.7) Screen just after running ( C-C ).
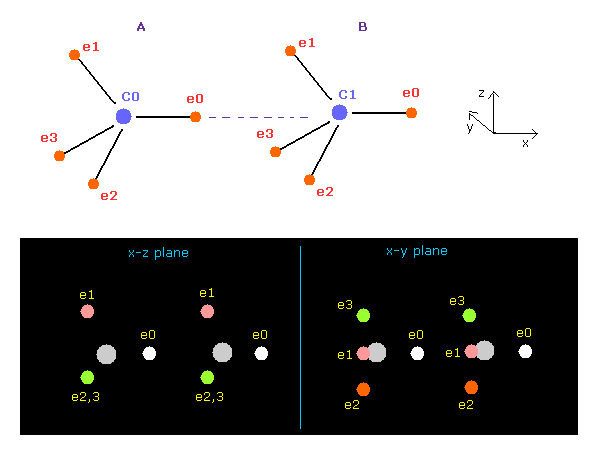
In this page, we proved when C-C bond length is the experimental value (= 1.5352 Å ), both carbon nuclei become stable using classical orbits and programs below.
Sample JAVA program, or
Sample program (text).
Save this text editor as "twoato.java", and compile it, neglect note, "-Xlint : unchecked ---".
Here new unit of 1 MM = 10-14 meter is used.
(Fig.8) C-C bond length is experimental value = 1.5351 Å
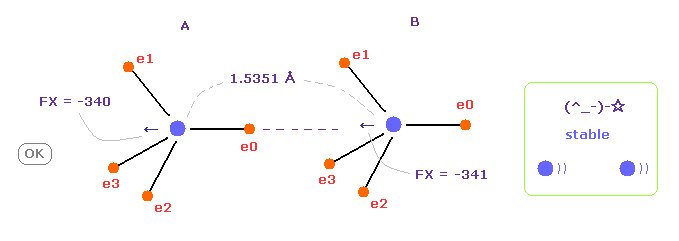
When C-C bond length is experimental value, forces acting on A and B carbon nuclei are almost same.
( FX = -340 and -341 ).
This means C-C bond length is in equilibrium and stable.
Carbon's electrons are orbiting, and repeat ( flip ) A and B states, and the difference between -340 and -341 is almost zero, so, C-C bond length does NOT change, and stable in this state.
And this result shows Coulomb and de Broglie relations are effective also in actual C-C bond.
| C-C (MM) | A nuc FX | B nuc FX | Difference |
|---|---|---|---|
| 12000 | -856 | -1703 | -847 |
| 13000 | -633 | -1013 | -380 |
| 14000 | -479 | -627 | -148 |
| 15000 | -370 | -399 | -29 |
| 15351 | -340 | -341 | -1 ← |
| 16000 | -292 | -258 | +34 |
| 17000 | -234 | -168 | +66 |
| 18000 | -191 | -109 | +82 |
| 19000 | -158 | -69 | +89 |
Table 1 shows, when C-C bond length becomes shorter than the experimental value (= 15351 MM ), attractive force of "e0" electron is too strong.
On the other hand, when C-C length becomes longer, repulsive force between both nuclei becomes dominant.
(Fig.9) Force = 1000.
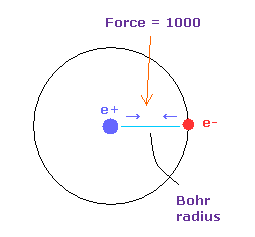
Force unit is shown in Fig.9.
The force between electron and nucleus in H atom ground state is supposed to be "1000".
So when the distance between electron and +e nucleus is Bohr radius, its force becomes 1000.
For example the force of 1468 is 1.468 times that in H atom ground state.
According to Virial theorem, the potential energies of free two C atoms becomes -148.025 × 4 = -592.1 eV (= free ).
( Here 148.025 eV is total energies requiring ionization of all 1-4 carbon's valence electrons. )
So the binding energy of Fig.7 becomes ( 596.7 (= tV ) - 592.1 ) × 0.5 = 2.3 eV, which is close to the experimental value of 3.5 eV (= 346 kl/mol )
You can get exact 3.5 eV binding energy, if you shrink some of carbon's electron orbit a little, considering attractive force of nuclei around them.
Because this difference of 1.4 eV is very small in comparison with 1-4 total ionization energies (= 148.025 eV ).
( Of course, due to tetrahedral arrangenment of surronding nuclei, carbon's four electrons are almost balanced. )
After running program above, choose "C" (= carbon ) as "A atom".
And choose various atoms as "B atom", and investigate their influences on carbon electron "ele 0".
(Fig.10) Comparison of forces acting on C electron.
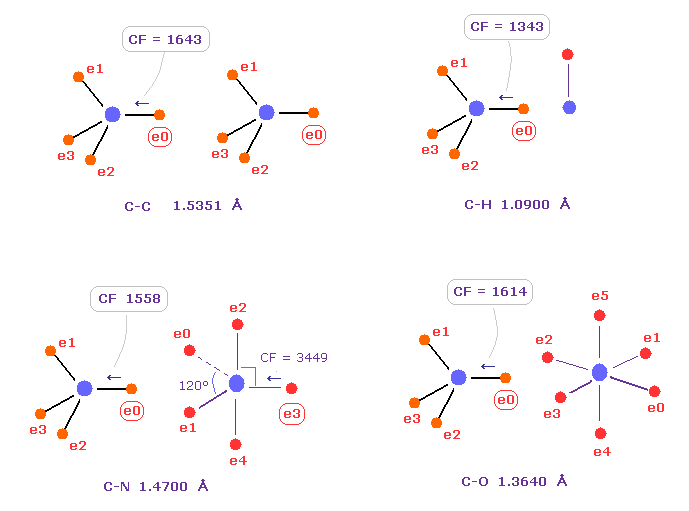
Fig.10 shows forces acting on carbon electron "e0" in C-C, C-H, C-N and C-O single bonds.
Considering carbon can keep tetrahedral structure in various bonds, it is natural forces acting on C electron are almost equal to each other.
Actually, these forces (= CF ) are 1643, 1343, 1558, 1614 in different C-C, C-H, C-N, C-O bonds, respectively.
( These bond lengths are average experimental values. C-O single bond is from acetic acid. )
| molecular bond | bond length | Force on e0 |
|---|---|---|
| C - H | 1.0900 Å | CF = 1343 |
| C - C | 1.5351 Å | CF = 1643 |
| C - N | 1.4700 Å | CF = 1558 |
| C - O | 1.3640 Å | CF = 1614 |
| C - F | 1.3500 Å | CF = 1605 |
| C - Si | 1.8500 Å | CF = 1602 |
| C - P | 1.8400 Å | CF = 1584 |
| C - S | 1.8200 Å | CF = 1708 |
| C - Cl | 1.7700 Å | CF = 1626 |
Table 2 shows forces (= CF ) acting on carbon electron "ele 0" in various bonds.
Surprisingly, in different bonds, these forces (= CF ) become almost same !
This means common mechanism is working, and carbon's tetrahedral structure is kept in various bonds.
Valence electron "e0" of Fig.10 comes closest to other nucluei, so this electron is most affected by other nuclei.
This means this valence electron's stability is one of crucial factors in determination of bond length.
(Fig.11) Unrealistic quantum chemistry NEVER considers nuclear and electron stability.

In quantum mechanics (= chemistry ), each electron is very vague and spreading into infinity.
In classical orbits of Fig.7, we can easily get bindng energy, avoiding electrons between C-C nuclei.
But of course, in quantum chemistry, we cannot use this very easy way.
They "always" have to use very complicated mathematical determinant to express electrons avoiding each other, because two electrons cannot be in the same state in determimants.
They stretch the original Pauli exclusion principle too much to express these repulsive electrons.
(Fig.12) Choosing proper basis set for each atom is most important for quantum chemistry.
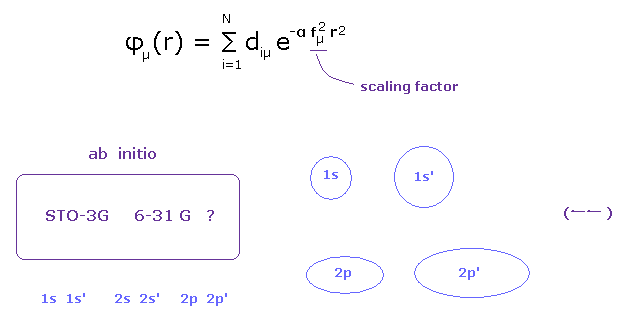
And due to these unrealistic concept of wavefunction, they cannot consider very important concepts such as stability of nuclei and valence electrons.
All they can do is to see "energy".
But binding energy is much smaller than ionization energies of atoms.
( For example, in C-C bond, 3.5 eV = bond energy, 296.05 eV = 2 × 1-4 ionization energy of carbon. )
So we can easily manipulate these very small bond energy by artificial choice of basis sets.
Stability of nuclei and valence electrons themselves are much more important and crucial factors in determinations of bond length and angles, as shown in this page.
(Fig.12') Integer times de Broglie wavelength is kept in quantum chemistry.
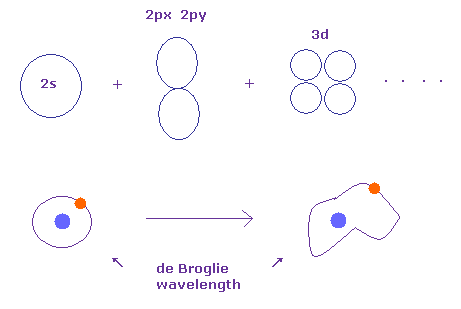
As you know, Schrodinger's wavefunctions can give completely same energy levels as Bohr model.
This means Schrodinger's wavefunctions basically depends on the same integers times de Broglie wavelength. See also this page. )
When we change the charge Z part of Schrodinger's exponential wavefunction, orbital shapes can be changed freely, keeping integers times de Broglie wavelength.
As shown in this page, when charge part of wavefunction is equal to actual charge at that location, potential energy becomes the lowest, due to Virial theorem.
As you see in Fig.12', if we can freely change orbital shapes ( keeping de Broglie wavelength ), their potential energies can be manipulated freely under some limitation (= integer times de Broglie wavelength ).
Qauntum mechanics cannot consider real electon's motion, so all we have to do is to see energy.
As a result, we can arificially manipulate potential energy, changing orbital shapes.
(Fig.13) H2 molecule.
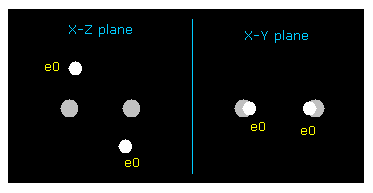
As shown in this page, we have succeeded in expressing hydrogen molecule using Bohr's orbit.
Actually when we aim at the stability of both A and B nuclei ( FX = 0 ), and average de Broglie wave is "1.0000" ( ave = 1.0000 ), we can explain the true meaning of H2 bond length, running this program.
| internuc (MM) | A-X (MM) | A-Z (MM) | B-X (MM) | B-Z (MM) | Force | aver waves | total V (eV) | bond energy |
|---|---|---|---|---|---|---|---|---|
| 6000 | 1870 | 4972 | -1870 | -4972 | 0 | 1.0000 | -60.664 | 3.120 |
| 6500 | 1145 | 4827 | -1145 | -4827 | 0 | 1.0000 | -62.204 | 3.890 |
| 7000 | 830 | 4755 | -830 | -4755 | 0 | 1.0000 | -62.893 | 4.234 |
| 7200 | 745 | 4739 | -745 | -4739 | 0 | 1.0000 | -63.014 | 4.295 |
| 7414 | 669 | 4729 | -669 | -4729 | 0 | 1.0000 | -63.056 | 4.316 |
| 7600 | 610 | 4724 | -610 | -4724 | 0 | 1.0000 | -63.047 | 4.311 |
| 7800 | 560 | 4721 | -560 | -4721 | 0 | 1.0000 | -63.010 | 4.293 |
| 8000 | 518 | 4720 | -518 | -4720 | 0 | 1.0000 | -62.952 | 4.264 |
| 9000 | 360 | 4741 | -360 | -4741 | 0 | 1.0000 | -62.365 | 3.971 |
As shown in Table.3, when the bond length of H2 molecule is the experimental value of 0.7414 Å (= 7414 MM ), total V is the lowest, and binding energy becomes biggest (= 4.316 eV ), which is good.
This result clearly shows H2 bond length is 0.7414 Å from the viewpoint of classical orbits.
Hydrogen ionization energy (= 13.606 eV ) is not so big in comparison with H2 bond energy.
So considering this bond energy is important.
We can explain not only H2 bond energy, but also stability of nuclear and electrons using classical orbits !
In quantum chemistry, we need to use functions which include r12 (= distance between two electrons ), and manipulate these interelectron distances.
Because, there are limits only in determinants to express repulsive electrons.
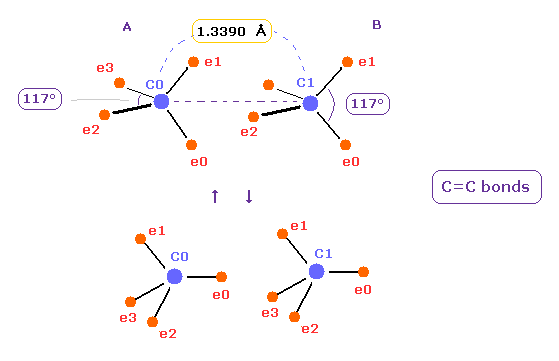
(Fig.14) C=C double bonds ?
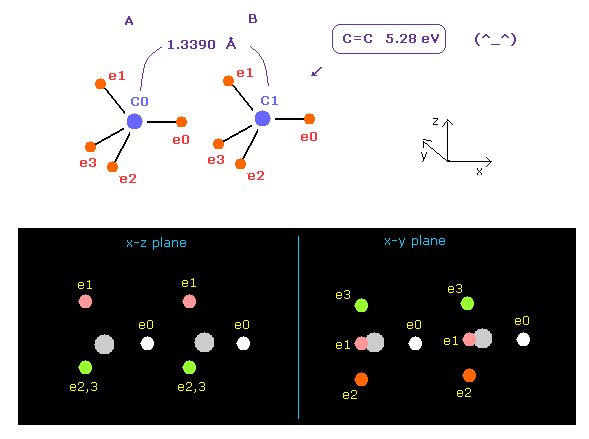
After running program above, input "13390", and click "internuc" button.
The experimental value of C=C double bonds are 1.3390 Å (= length ), and 602 kJ/mol (= 6.24 eV ).
In Fig.14 case, total potential energy becomes -602.652 eV, so bond energy becomes ( 602.652 - 592.1 (= free C,C ) ) / 2 = 5.27 eV, which is almost same as the experimental value.
( This small difference is gone by shrinking some of carbon's electron orbit a little. )
But in Fig.14 case, force acting one each carbon nucleus is FX=-566, and FX=-836, which means they attract each other too much.
(Fig.15) Bond length and bond angle of ethylene.
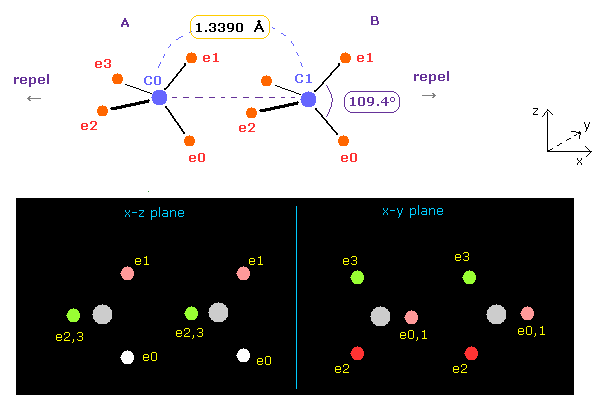
Rotates both A and B atoms by -54.7 degree in x-z plane.
( Input -54.7 into textbox and click "x-z ang" button. See also this page. )
In this state, ele 0,1 become parallel to z axis, and ele 2,3 become parallel to y axis.
In this case, both C nuclei repel each other by the force FX = 359.
(Fig.16) Bond length and bond angle of ethylene.
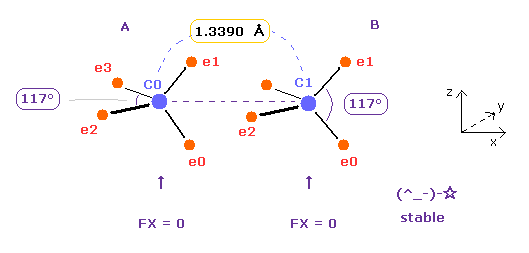
In Fig.15, angle between carbon valence electrons are kept to be the original 109.4 degree.
So we change e2-n2-e3 angle of carbon A, and e0-n-e1 angle of carbon B atom to 117 degree (= experimental value of H-C-H angle ).
See Table 4, input "3324" and "5487" into the appropriate textboxes and press enter key.
If so, repulsive force between two carbon nuclei becomes just zero, and stable.
| eNo. | +X (MM) | +Y (MM) | +Z (MM) | nuc (MM) | CF | Waves |
|---|---|---|---|---|---|---|
| A ele 0 | 3706 | 0 | -5235 | 6414 | 2162 | 1.976 |
| - ele 1 | 3700 | 0 | 5239 | 6413 | 2162 | 1.976 |
| - ele 2 | -3324 | -5487 | 0 | 6415 | 2272 | 2.023 |
| - ele 3 | -3324 | 5487 | 0 | 6415 | 2272 | 2.023 |
| B ele 0 | 3324 | 0 | -5487 | 6415 | 2272 | 2.023 |
| - ele 1 | 3324 | 0 | 5487 | 6415 | 2272 | 2.023 |
| - ele 2 | -3703 | -5237 | 0 | 6413 | 2162 | 1.976 |
| - ele 3 | -3703 | 5237 | 0 | 6413 | 2162 | 1.976 |
| internuc (MM) | A nuc FX | B nuc FX | total V (eV) | A e2-n-e3 | B e0-n-e1 |
|---|---|---|---|---|---|
| C=C 13390 | 0 | 0 | -594.36 | 117 deg | 117 deg |
As shown in Table 4, when the angle of e2-nuc-3 in A atom and e0-nuc-e1 in B atom are just 117 degree (= experimental value ), Force (= FX ) acting on each nucleus becomes just zero.
This means two nuclei of C=C bond becomes stable.
The repulsive force in C=C bond is stronger than C-C, so bond angles of outer valence electrons need to to be wider.
The problem is in Fig.16 state, bond energy becomes only 1.7 eV.
(Fig.17) Oscillation between different states in C=C bonds.
Considering proper bond energy of Fig.14 and stable nuclei of Fig.16, two carbons in C=C are thought to be oscillating between different states of Fig.17.
Complex motions of Fig.17 are true states of C=C double bonds. ( So it's not so simple. )
In upper case of Fig.17, carbon electrons tend to be attracted to two hydrogens outside.
In the lower, they are attracted to another carbon nucleus.
Of course, even in Fig.16 case, due to the decrease in kinetic energy or attraction of four electrons between C=C, bond energy are thought to be kept.
(Fig.18) C = C ( pi ) bond is real ?
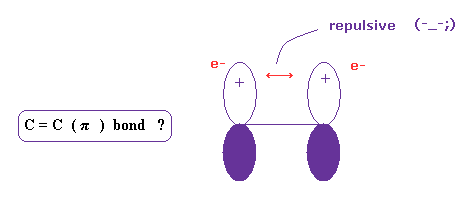
Four hydrogen atoms of ethylene are on the same plane.
Quantum chemistry insist this is due to pi bond, in which two 2p orbitals form a pair.
But this explanation is strange, because it is natural that two negative electrons are repelling each other.
And basically, as I explain above, it cannot reach experimental bond energy, when each electrons point in the same direction.
What on earth is this mysterious and unreasonable force violating basic Coulomb force ?
(Fig.19) Pair of "shortened" and "extended" orbits are stable.
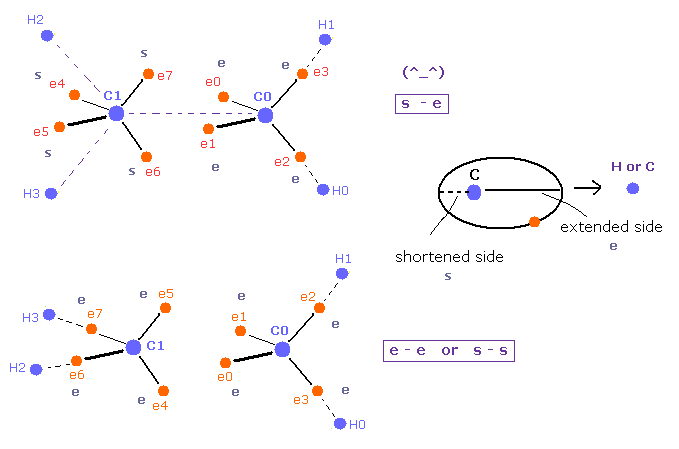
Carbon valence electrons are orbiting around C nucleus.
Basically these electrons are slightly extended to H or C nuclei.
In the upper of Fig.19, shortened (= s ) and extended (= e ) electron's orbits are facing each other between C=C nuclei.
( So one side is extended, and another side is avoiding. )
But in the lower of Fig.19, both sides are extended ( "e" and "e" ), or both are shortened ( "s" and "s" ).
So bond states are a little more unstable than the upper figure due to their mismatch, I think.
This explanation is more natural than strange pi bond, because, this obeys basic Coulomb force.
(Fig.20) C ≡ C triple bonds.
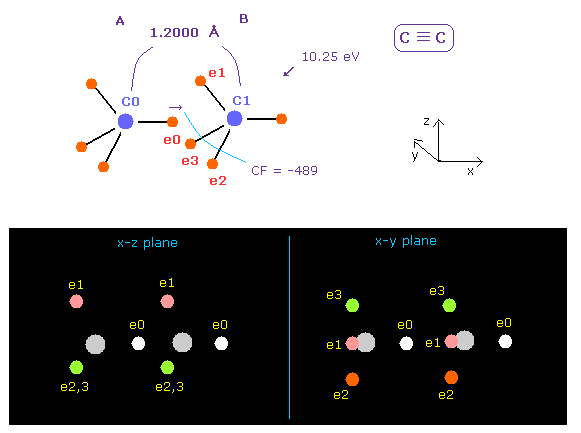
C≡C bond length of acetylene is 1.2000 Å.
After running program above, input "12000", and click "internuc" button.
If so, total potential energy (= tV ) becomes -612.634 eV, so the bond energy is ( 612.634 - 592.1 ) / 2 = 10.25 eV, which is a little bigger than the experimental value of 8.65 eV.
Actually C≡C bond length of 1.2000 Å is a little shorter than 2 × carbon electron orbital radius (= 2 × 0.6415 Å = 1.2830 Å ).
So the force CF acting on "e0" electron becomes negative (= -489 ), which means e0 electron of A atom is attracted to B atom.
Of course, this is weird.
We need to consider the fact three valence electrons of carbon B ( e1 - e3 ) are attracted to C0 nucleus and repelling "e0"
(Fig.21) C ≡ C triple bonds.

Considering repulsive interaction, when we rotate e0 electron by the angle of 10 degree on x-z plane, we can get almost same bond energy (= 8.5 eV ) as the experimental value (= 8.65 eV ).
In this case, total potential energy is -609.187 eV, so bond energy is ( 609.187 - 592.1 ) / 2 = 8.5 eV.
(Fig.22) C ≡ C triple bonds, tetrahedron is broken.
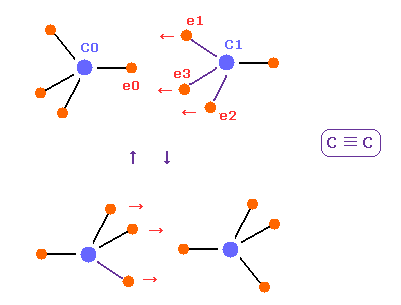
In acetylene ( HC≡CH ), there are only two hydrogen atoms.
So three valence electrons of each carbon are all coming close to another carbon nucleus.
So tetrahedral structure is more broken, ovecoming internal repulsive forces among four electrons.
Due to these three electrons ( e1-e3 ) of another carbon, e0 electrons of C0 is repelled, and can return to its original orbit.
Of course, because of this broken tetrahedral symmetrical structure, C≡C bonds are easily changed to double or single bonds.
Considering force CF and stability of electron "e0" in Fig.20 and Fig.21, this bond length of 1.2000 Å is the lower limit.
(Fig.23) C-H bond energy = 4.0 eV.
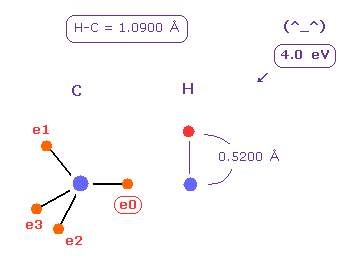
Average C-H bond length is 1.0900 Å.
After running program above, input "10900", and click "internuc" button.
Then choose C and H atoms as A and B atoms, respectively.
Input "5200" (= about Bohr radius ) into "+Z (MM)" textbox of B atom, and press enter key.
In this state, total potential energy (= tV ) becomes -331.169 eV.
And total potential energy of free carbon and hydrogen atoms is ( -148.025 (= 1-4 ionization ) - 13.606 ) × 2 = -323.262 eV using Virial theorem.
So the bond energy is ( 331.169 - 323.262 ) / 2 = 3.95 eV, which is almost same as the experimental value of 4.25 eV.
(Fig.24) C-H bond length is stable.
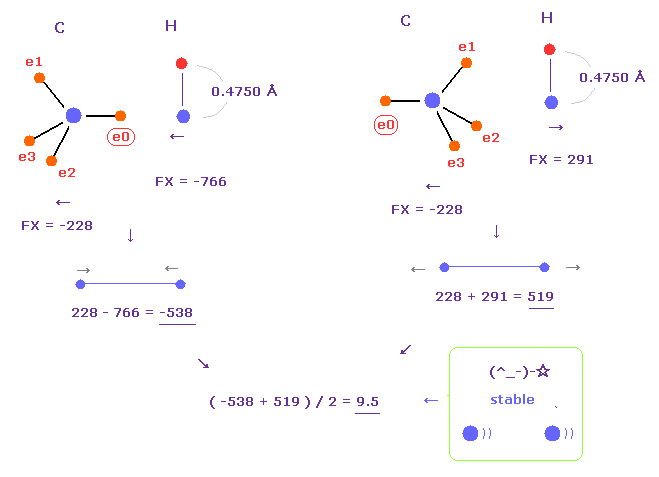
In Fig.23, e0 electron is close to hydrogen, so hydrogen electron is repelled and Bohr radius gives good bond energy.
But actually, hydrogen orbital shrinks a little due to attractive force of carbon.
If we choose "4750" as hydrogen electron's +Z (MM), average de Broglie waves becomes almost 1.0.
In this case, average forces (= FX ) between carbon and hydrogen nuclei becomes almost zero (= 9.5 ).
Because carbon nucleus is repelled, and hydrogen nucleus is attracted to e0 electron, which cancels out the repulsive force.
As a result, like C-C bond length, C-H bond length is stable when it's 1.0900 Å.
Sample JAVA program (= ethane. )
Sample JAVA program (= ethylene. )
These are sample JAVA program to visualize ethane and ethylene molecules.
Save these text as "etham.java" or "ethylen.java", and compile them.
Manipulating methods are completely same as this page.
In this program, we just show original atoms as they are, and don't take average electron's motion ( of Fig.24 ).
So I plan to change this program in the future to express these average electron motions.
(Fig.25) Replusive force in N-H bond.
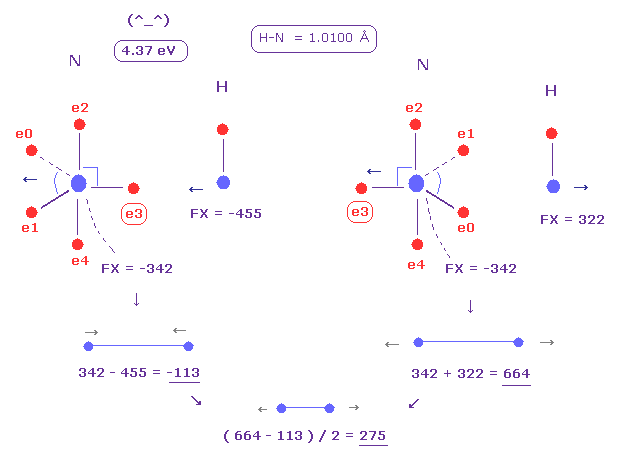
Average N-H bond length is 1.0100 Å.
After running program above, input "10100", and click "internuc" button.
Then choose N and H atoms as A and B atoms, respectively.
In this state, total potential energy (= tV ) becomes -569.68 eV.
And total potential energy of free nitrogen and hydrogen atoms is ( -266.95 (= 1-5 ionization ) - 13.606 ) × 2 = -561.11 eV using Virial theorem.
So the bond energy is ( 569.68 - 561.11 ) / 2 = 4.285 eV, which is almost same as the experimental value of 4.00 eV.
( So in this case, nitogen's electron is a little repelled by hydrogen's electron. )
And the average repulsive force between N-H bond becomes 275, as shown in Fig.25.
(Fig.26) Replusive force in C-N bond.
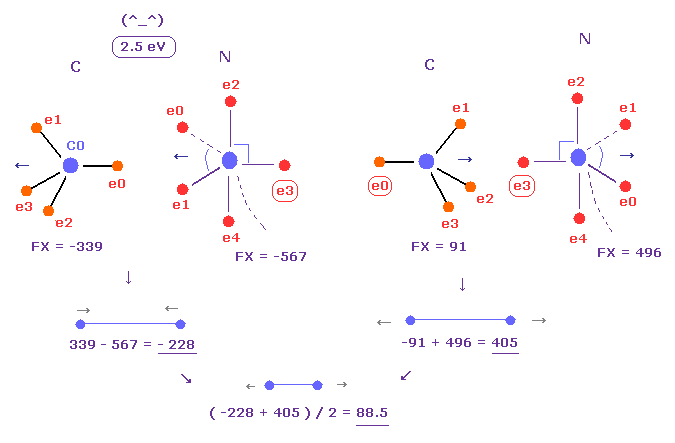
Average C-N bond length is 1.4700 Å.
After running program above, input "14700", and click "internuc" button.
Then choose C and N atoms as A and B atoms, respectively.
In this state, total potential energy (= tV ) becomes -834.84 eV.
And total potential energy of free nitrogen and carbon atoms is ( -266.95 (= 1-5 ionization ) - 148.025 (= 1-4 ionization) ) × 2 = -829.9 eV using Virial theorem.
So the bond energy is ( 834.84 - 829.9 ) / 2 = 2.5 eV, which is almost same as the experimental value of 3.1 eV.
( So in this case, electron's orbits shrink a little by attractive nuclei. )
And the average repulsive force between C-N bond becomes 88, as shown in Fig.26.
(Fig.27) Force balance in peptide pond.
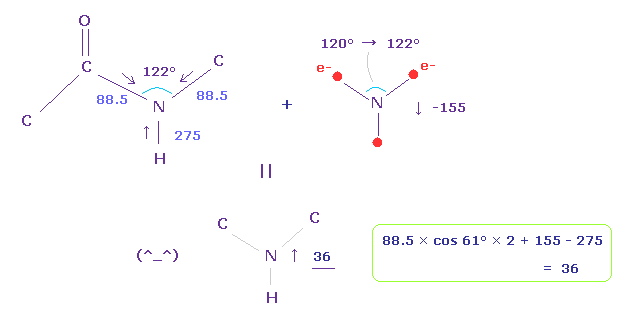
So basically, the repulsive force of N-H bond (= 275 ) is stronger than that of N-C bond (= 88.5 ).
Peptide bond is known to be on the same plane, and its C-N-C angle is about 122 degree.
We consider force balance using Fig.25 and Fig.26, and widen the angle of N valence electrons from 120 → 122 degree.
In this case, force acting on N nucleus becomes 36, which is almost zero, and stable.
Basically, due to the stronger "pushing" force in N-H bond, ammonia (NH3) is distorted and cannot be on the same plane.
(Fig.28) Pubchem 3D SDF structure of H2SO4.

In this section, we utilize Pubchem 3D molecular structure data of NIH, which is a good source of small molecules.
See Pubchem site, and searching for a word of "sulfuric acid".
After displaying sulfuric acid site, click "3D: SDF: Display" at the upper right.
The data of Fig.28 is displayed on the screen, so copy and paste the text surrounded by blue line into some text editor.
And save this text file in some folder.
(Fig.29) 3D coordinates and neighboring atomic data of H2SO4.

Basically, upper part of Fig.29 shows x, y, z coordinate ( Å ) of each atom.
And lower part of Fig.29 shows informations about neighboring atomic number.
For example, neighboring atoms of atom 1 (= S ) are 2 (= O ), 3 (= O ), 4 (= O, double ), 5 (= O, double ).
Sample JAVA program ( utilizing pubchem data. )
(Fig.30) Change location folder name inside the program.

When you save this text editor at some different folder,
change location address at which you save this text inside the upper program.
( Change blue line of Fig.30. )
(Fig.31) Molecular structure of H2SO4.
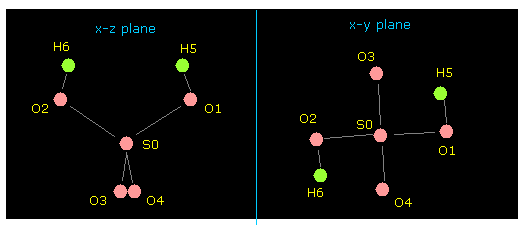
After running this program, picture of Fig.31 is displayed on the screen.
Manipulating methods are the same as this page.
(Fig.32) Stability of H2SO4.
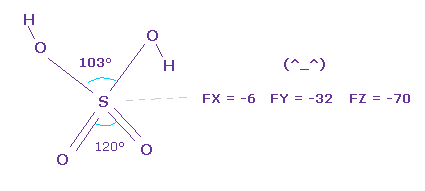
As you see force component acting on central sulfur of H2SO4, they are almost zero.
So the sulfur nucleus is stable.
Pubchem data is a little different from CRC structure data, but they are almost same.
In the program above, a point electron of each atom turns in the direction of lower-number atom at initialization.
So try changing these electrons' distribution in each atom to express various bonds.
(Fig.33) Bond energy of S=O.
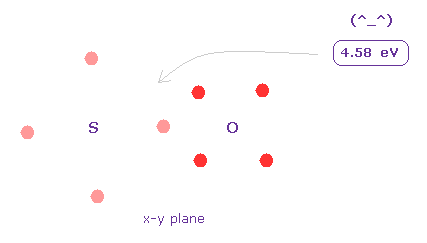
Average S=O double bond length is 1.4300 Å.
After running program above, input "14300", and click "internuc" button.
Then choose S and O atoms as A and B atoms, respectively.
In this state, total potential energy (= tV ) becomes -1428.064 eV.
And total potential energy of free sulfur and oxygen atoms is ( -276.36 (= 1-6 ionization ) - 433.1 (= 1-6 ionization) ) × 2 = -1418.9 eV using Virial theorem.
So the bond energy is ( 1428.064 - 1418.9 ) / 2 = 4.58 eV, which is almost same as the experimental value of 5.41 eV.
( So in this case, electron's orbits shrink a little by attractive nuclei. )
Next we investigate nitric acid (= HNO3 ), using pubchem data.
Like Fig.29, we get the follwing structure data from the pubchem.
Save this text at the folder of "C:\sdff" as the filename of "nitric-acid.text".
(Fig.34) Changing address inside program.

So we change the program above like Fig.34.
Here we use this program.
Save this program as "sdfd2.java", and compile it.
(Fig.35) Force balance of N nucleus.
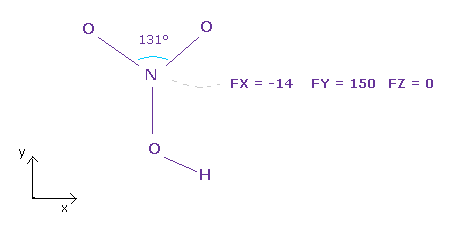
After running the program above, input "3" (= nitorgen ) into textbox, and click "top nucl" ( or "nucleus" ) button.
All atoms of the nitric acid is on almost same plane ( = x-y plane ).
As you see in Fig.35, total forces acting on N nucleus is almost balanced.
Force FY (= 150 ) is slightly bigger than other force components.
If you widen two valence electrons of nitrogen a little ( because 131 degree is wider than 120 degree ), this force FY can be cancelled out.
At initialization, oxygen electron points to that of nitrogen.
So rotate electrons of each oxygen by 45 degree to avoid repulsive force between them.
If so, N nucleus becomes more stable. Try it.

2013/5/19 updated. Feel free to link to this site.