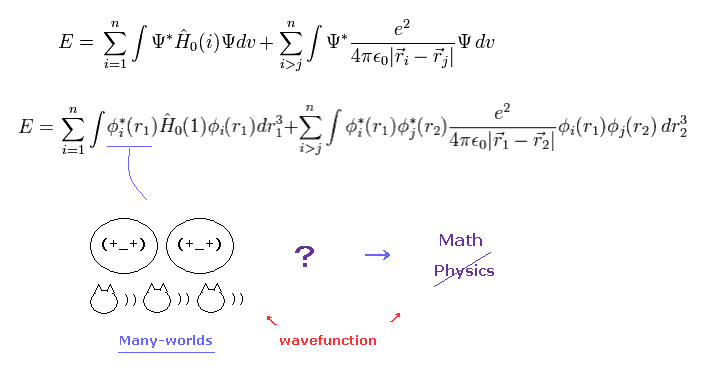
Top page (correct Bohr model including the two-electron atoms)
Manipulation and rotation of dihedral angles.
(Fig.1) More than 80 years have passed. → wavefunctions remain a "mystery" = useless. Why ?
Nobel prize in chemistry was sent to computational chemists.
Computational chemistry is very important to investigate actual molecular behavior, so this decision is very reasonable.
But in fact, "computational chemistry" is so unpopular that chemists ( and of course, biologists ) don't use this methods for actual research even in this 21th century.
Because, the present computational chemistry is not so useful in applied fields because they keep wavefunction (+ Pauli exclusion principle ) unknown.
The most serious problem is that they NEVER try to ask what these mysterious wavefunctions really are, though investigating them is indispensable for making computing methods much easier and useful.
They just repeat "Shut up and calculate !" about wavefunctions themselves.
Because the instant you try to ask what they are, you notice that they are unrealistic many worlds.
(Fig.2) More than 80 years have passed. → "Force" of Pauli exclusion principle remains a "mystery".

Spin is unrealistic, because the spinning speed leads to more than 100 times light speed ( > 100 × c ).
And spin magnetic moment is too weak to cause Pauli exclusion principle, as shown in this page.
Then what is the origin of the force in Pauli exclusion principle ?
Spin magnetic moment is too weak, so there is only one thing left to cause this strong power.
De Broglie wave ( interference ) is the origin of Pauli exclusion principle and ferromagnetism. ( See helium and this page. )
Unrealistic spin cannot cause real de Broglie wave, so all they can depend on is mathematical anticommutating operator.
As a result, they forbid us from asking what these anticommutation really are, and we only use very incovenient antisymmetric determinants (= Fig.2 ).
(Fig.3) DFT in condensed matter physics is only "rough" approximation.
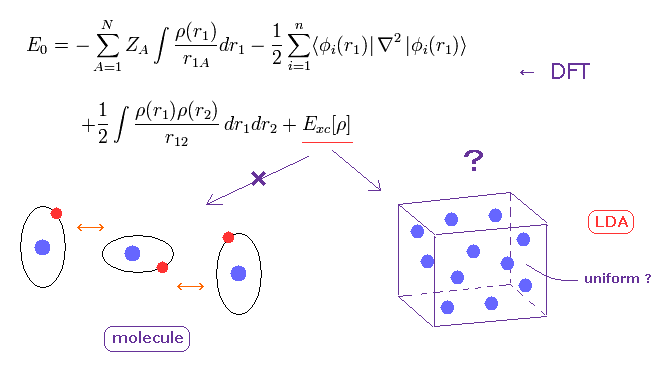
Density functional theory (DFT) is often used in condensed matter physics.
The important point is that DFT cannot determine very important part of exchange-correlation energy (= Exc ).
They often use local density approximation (LDA), which uses very rough approximation of uniform electron gas.
Of course, actual materials are NOT uniform, so they sometimes try to add some gradient of charge density (= GGA ).
We need to choose artificially some parameters to agree with experimental results in GGA.
So DFT itself is NOT ab-initio.
Furthermore, DFT is completely useless when we consider weak intermolecular forces in proteins.
(Fig.4) Molecular mechanics does NOT treat electrons.
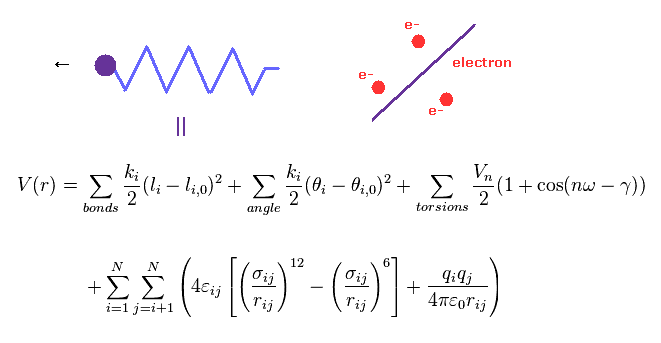
Molecular mechanics (MM) and dynamics (MD) use classical mechanics to model molecular system.
Due to very complicated quantum wavefunctions, molecular mechanics are usually used instead of quantum chemistry in large molecules.
In MM method, bond interactions such as length and angle are treated as classical "spring".
The most important problem is MM does NOT have concepts of " electrons ".
So these classical potentials must be estimated empirically (= NOT ab-initio ).
But, for example, there are 20 kinds of amino acids, so 5 connected amino acids have as many as 20 × 20 × 20 × 20 × 20 = 3200000 kinds !
So it is impossible to determine every combination without knowing true nature of molecular bonds.
(Fig.5) Why carbon atom (= hydrophobic ) dislikes water ?

It is known residues including only carbon and hydrogen atoms are hydrophobic.
Unfortunately, classical methods such as MM and MD cannot explain these mechanism correctly, because they have NO concept of actual electron's distribution ( and de Broglie waves ).
On the other hand, usual quantum chemistry cannot deal with these complicated molecules in which weak interactions are especially important .
As shown in this page, all four electrons of carbon are often bound to other atoms.
So these carbon cannot withstand repulsive force of oxygen, because carbons cannot adjust their free valence electrons against oxygen.
On the other hand, nitrogen and oxygen atoms have excessive electrons to deal with repulsive force.
(Fig.6) Electrons in benzene are periodically moving ( NOT superposition ! )
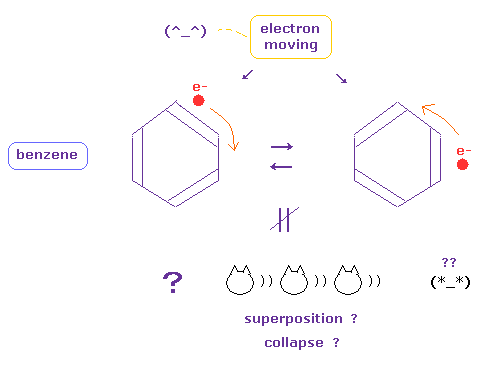
Quantum mechanics (chemistry) insist electrons of benzene ring are unrealistic superposition state.
The instant we admit this strange superposition and randam collapse, we must give up investigating more dynamic electron's motion.
Particles such as electron and ions are actually moving and oscillating, which causes various dynamical biological responses inside body.
If we admit these electrons of bensene are actually moving, we can use and combine various kinds of realistic particle's motions, collisions and interactions to construct nano-machines.
( Many worlds and faster-than-light collapse cannot be used at all as useful nano-machine, because they are unreal. )
(Fig.7) Depending on binary numbers in conventional computer has already reached its limits.

In usual computers, the program languages (= commands ) are changed into binary number (= "0" or "1" ).
And they work based on these very simple numbers by repeating reading them in order.
This speed is fast for some computing, but when you try to compute a large number of atoms, it takes extremely much time.
As you know, actual living things consist of a large number of atoms, but their biological functions are working stably and correctly. ( Their basic speed is fast, too. )
Of course, these organisms don't use binary numbers at all.
This means basic molecular interactions among dynamic electrons and ions have much higher potentials to give high-efficient nano machines than conventional computers.
To realize it, we have to consider actual molecular dynamic motions and interactions, giving up very unrealistic ( useless ) concepts such as wavefunction "collapse", many-world like superpositions, and uncertainty principle.
(Fig.7') Condensed-matter → chemistry → "complicated" molecular biology = Benefit order.
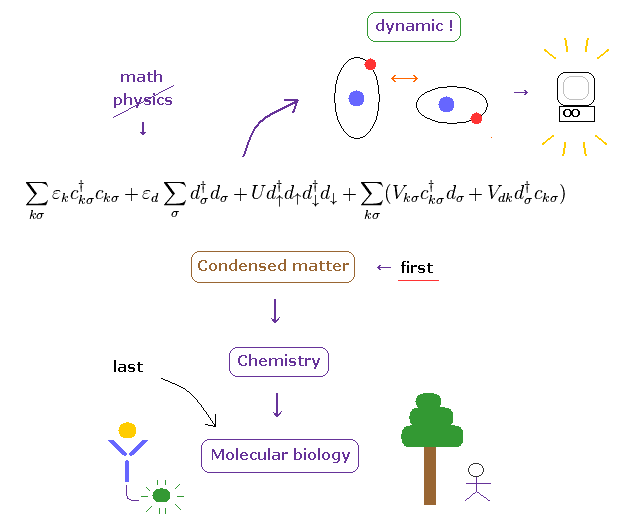
As you know, living things on the earth have very sophisticated, complicated and accurate nano- biological functions, which complexity is much greater than simpler condensed-matter and crystals.
So if you try to take advantage of realistic dynamical molecular interaction, instead of fantasied and useless superposition (= many-worlds ), you need to correct simpler condensed-matter physics first.
To accomplish it, you need to clarify the mysterious force of Pauli exclusion principle, giving up abstract math symbols.
( The instant the force of Pauli exclusion can be clarified, unreal spin would disappear. )
Lastly, very complicated molecular biology benefits from this drastic change, and serious disease such as ALS, dementia, and autoimmune disease could be treated.
Till then, it is very difficult that the present molecular biology is useful for our actual lives.
(Fig.8) How dihedral angles are changed by substrate in adenylate kinases ?
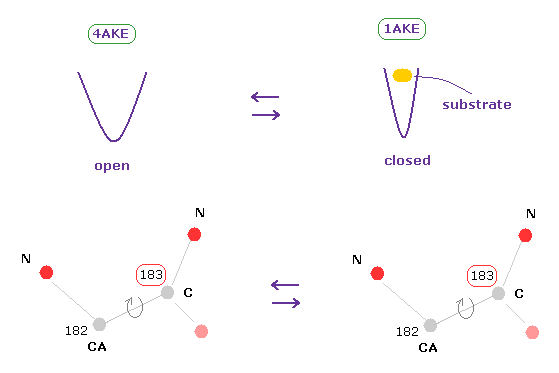
Adenylate kinase (AK) is a phosphotransferase enzyme that catalyzes the interconversion of adenine nucleotides. (ADP, ATP, and AMP)
AK is known to have two conformations of open and closed ( PDB 4AKE, 1AKE, respectively ).
Substrates such as ATP are bound to closed type AK.
Sample JAVA program to compare dihedral angles.
The whole protein conformation is determined by each dihedral (torsion) angle.
So we investigate how each dihedral angle changes by this conformational transitions using sample program above.
(Fig.8') Dihedral angles mean most stable positions. ( residue "56" CA carbon ↓ )

Due to the existance of substrate, the dihedral angles of the first (= 4AKE ) and second (= 1AKE ) proteins prove to be a little different in most sites, as is computed by the program above.
In spite of this difference, the common point is that their angles are the most stable positions in both proteins, as I explain here.
When you rotate by ±10 degree from the original angles, some atoms crash into each other, and block their rotations.
This fact clearly proves that the existence of extremely short interatomic length determines each dihedral angle in both proteins, like in this page.
(Fig.9) Save three files and designate saving folder.
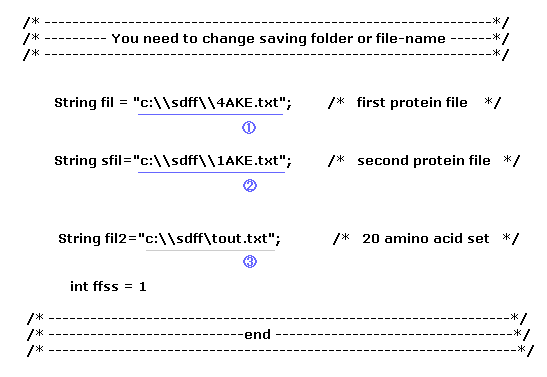
Before running this program, you need to save three kinds of text files to some folder of your computer.
The first file (= 1 ) is the first AK protein (= 4AKE.txt, open ), and the second file is the second AK (= 1AKE.txt, closed ).
Furthermore, save 20 amino acid template file (= tout.txt ), which is used for chaging one amino acid, as shown in this page.
AK protein ( open, 4AKE.txt )
Ak protein ( closed with substrate, 1AKE.txt )
20 amino templates ( tout.txt )
Fig.9 ( first line ) means you save the file at the location of "C:\sdff" folder as the filename of "4AKE.txt".
When you change these file name, or save them in a different folder, change Fig.9 part ( blue or gray line ) inside program above.
( Of course, you can save these PDB files directly from PDB website, too. )
(Fig.10) After running program.

After saving three data files of Fig.9, run the sample program above.
This class file name is "crash", so save this program "crash.java" and compile it.
You can run the program, as it is, neglecting notes such as "Recompile with -Xlint: unchecked for details ".
First, we compare all dihedral angles (= C, CA parts ) of these two conformational changed AK proteins.
Input "1" (= no ), and press enter key about the first question (= Rotate all angles ), and input "0" (= yes ), and press enter key about the second question (= Compare angles ).
Total atom ( second, first ) means total atomic number ( including hydrogen ) of each first, or second AK proteins.
( Each AK has two subunits A and B. )
(Fig.11) Dihedral angles at various parts.
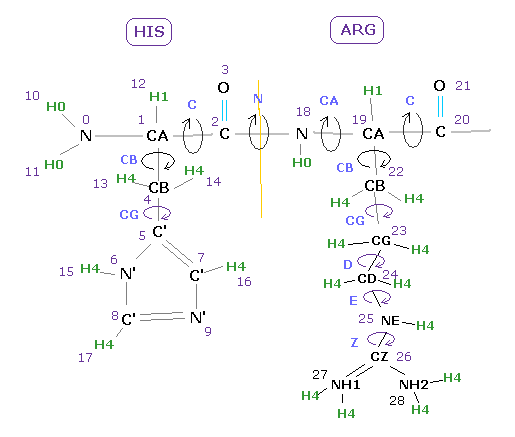
In some amino acids, there are various rotation sites, as shown in Fig.11.
The most important are dihedral angles of "CA" and "C" sites, which belong to main chain.
( "N" site angle is fixed as almost 180 degree, due to its double bond like property ).
In this program, we compute each CA or C corresponding dihedral angle of the first and second AK proteins, and subtract first protein angle from second one ( result = 2nd angle - 1st angle ).
For example, "5C=13.5" means the difference between "C" angles ( at residue "5" ) of second and first AK proteins is 13.5 degree.
( So the dihedral angles at this site are almost same in second and first AK proteins. = difference is only 13.5 degree. )
(Fig.12) Comparing each dihedral angles. (= Second protein minus first protein. )

Amino acid of residue number "56" is "GLY" in both AK proteins.
Dihedral angles of "CA" site in this GLY are 67.9 and 90.8 degrees, in first (=4AKE ) and second (= 1AKE ) proteins.
As a result, the difference becomes 90.8 - 67.9 = 22.9 degree.
When these differences between the first and second corresponding sites are less than 10 degree, this atomic site is not shown.
( For example, residue "9" is not shown in Fig.12, which means the dihedral angles of residue "9" are almost same in the first and second AK proteins. )
We investigate what these differences mean, by seeing these sites directly.
(Fig.13) Narrowing y and z width.
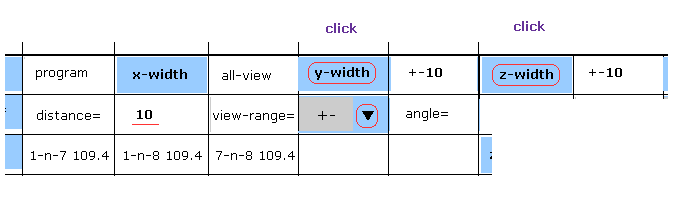
On the screen, all atoms of AK proteins are displayed, so it is difficult to grasp their relations.
As I explanied in this page, if we narrow regions in each directions, it becomes easier to see.
Choose "+-" in the scroll bar, input "10" into the textbox next to "distance=".
And then click "y-width" and "z-width" buttons.
Furthermore, if you click "hydrogen" button to erase hydrogen atom, the screen becomes more easier to see.
(Fig.14) Protein picture example.

Fig.14 is an example of some protein.
The designated atom is displayed as yellow square (= carbon-183 in Fig.14 ).
For example, on x-z plane, only region within ±5 Å in the y direction is shown.
You can move or rotate the whole protein by clicking each triangle or circles on the edge.
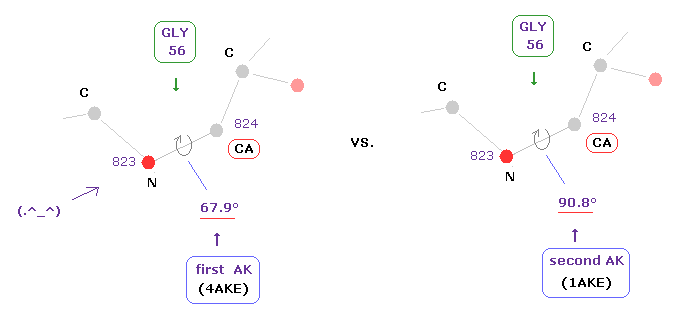
(Fig.15) First AK protein -- residue 56, CA site.
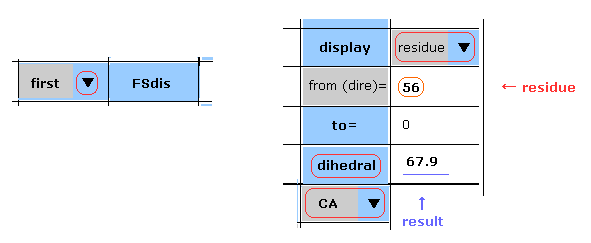
Manual are almost same as this page.
In Fig.15 case, you display the "CA" dihedral angle of residue "56" amino acid in the first AK protein.
Choose "first", "residue" and "CA" in each scroll bar, input "56" as residue number into textbox ( next to "from (dire)=" ), and then click "dihedral" button.
The dihedral angle of this site proves to be 67.9 degree.
(Fig.16) 1st AK protein -- distance between A and B atoms ( < 3.5 Å )
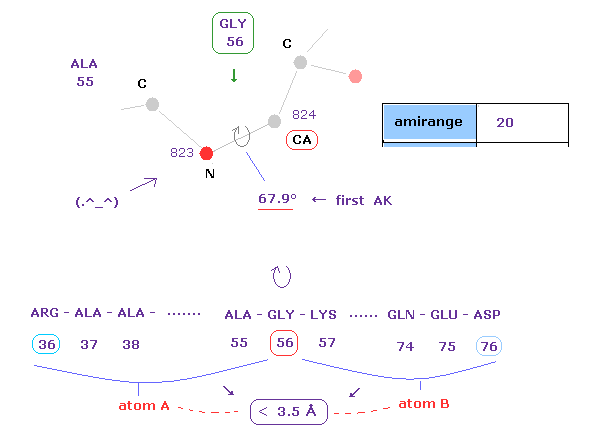
Like this page, this program gives interatomic distance less than 3.5 Å between A and B atoms.
( Caution: these A, B don't mean "subunit" only here. )
Atom A belongs from residue 36 (= 56-20 ) to residue 56 (= before CA ).
Atom B belongs from residue 56 (= after CA ) to residue 76 (= 56+20 ).
If you change the value of "amirange", you can change this residue range.
After rotating this 56-CA site, some atoms between A and B may crash into each other.
The important point is that each dihedral angle is determined by avoiding every single crash.
(Fig.17) 1st AK protein -- distance between A and B atoms ( < 3.5 Å )

In command prompt screen, these A-B interatomic distances ( < 3.5 Å ) are shown.
For example, the distance between oxygen of ILE (= atomic number 767 ) and nitrogen (= 830 ) of LYS is 2.733 Å.
You find this 2.733 Å is the shortest distance between A and B atoms in these values.
( All other distances are more than 3.0 Å )
"824" means the program atomic number (= not PDB number ) of CA atom in residue "56".
This program atomic number also includes hydrogen atom, which is bigger than PDB atomic number.
(Fig.18) 2nd AK protein -- residue 56, CA site.

Next we choose "second" in the scroll bar, and click dihedral button.
Dihedral angle of CA corresponding site in the second AK protein is 90.8 degree.
As a result, the difference is 90.8 - 67.9 (= Fig.15) is 22.9 degree.
This result is shown in command prompt screen ( 56CA = 22.9 ), as shown in Fig.12.
(Fig.19) 2nd AK protein -- residue 56, CA site.
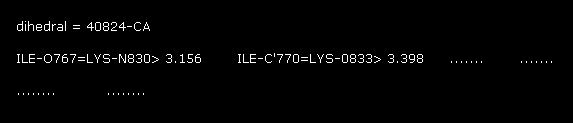
Like Fig.16, interatomic distances less than 3.5 Å between A and B atoms (= within ±20 aminoacids ) are shown in command prompt screen.
"40824" means program atomic number "824" in the second protein.
As shown in Fig.19, distance "3.156 Å" is the shortest in these values.
(Fig.20) What does this angle difference mean ?
Of course, some substrate is bound only to the second AK protein (= 1AKE ).
So it is quite natural that there are some differences in their dihedral angles.
By the way, are there other meanings in these differences ?
To investigate this reason, we rotate these angles by ±10 degree as shown in this page.
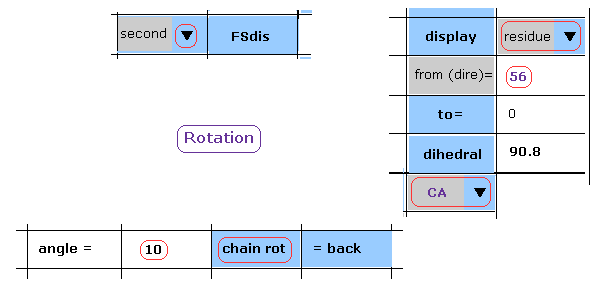
(Fig.21) Rotate dihedral angle (= first ) by 10 degree.
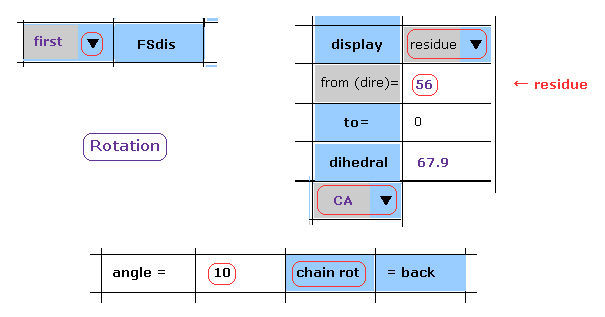
As shown in this page, we rotate dihedral angle.
Choose "first", "residue", and "CA" in the scrollbars.
Input "56" (= residue number ) and "10" (= rotation angle ) into the designated textboxes.
And then click "chain rot" button.
In this case, all atoms after CA carbon inside A subunit of the 1st AK protein are rotated by 10 degree around N-CA axis of Fig.20.
(Fig.22) Shortened interatomic distances after rotation.

After clicking "chain rot" button, shortened interatomic distances ( < 3.5 Å ) are shown in command prompt screen.
As shown in Fig.22, the interatomic distance between CB carbon of ALA (= 568 ) and C' carbon of LEU (= 1000 ) becomes much shorter to 1.789 Å from the original length of 3.921 Å.
This means these atoms almost crash into each other by this rotation.
Compare this 1.789 Å with the shortest length of 2.733 Å of the original (= Fig.17 ).
So this rotation is completely blocked.
(Fig.23) Shortened distance between CB-568 and C'-1000 atoms.

If you want to confirm this distance directly, input "1000" into textbox ( next to select button ), and click select button. ( after choosing "first" and "atom" in the scroll bars )
In this case, carbon atom of program atomic number "1000" is chosen as "selected" atom.
And then input "568" into the textbox ( next to "to=" ) and click "to=" button.
Text of atom 568 is shown in the textboxes above.
"1.7894" is shown in the column of "dis(A)" at the site of 568-CB-ALA.
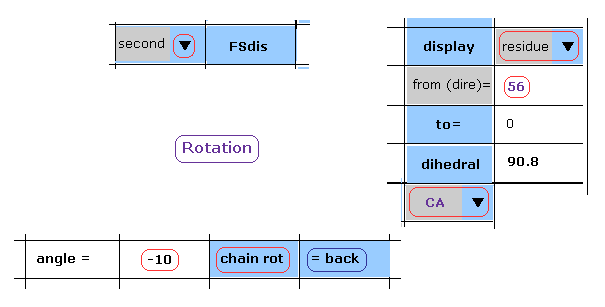
(Fig.24) -10 degree rotation is blocked, too.
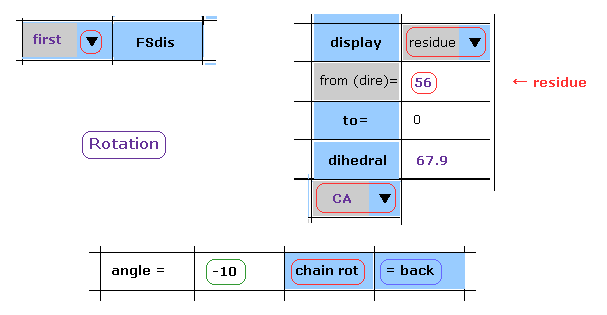
Next, click "back" button to the original angle.
Then, input "-10", and click "chain rot" button.
(Fig.25) Rotaion back → -10 degree rotation.

As shown in Fig.25, some interatomic distances become too short (= 2.005 Å, or 2.058 Å ).
This short length is shorter than the original shortest length (= 2.733 Å ) of Fig.17.
This means this -10 degree rotation is also blocked at this site.
(Fig.26) Rotations are blocked in both directions.
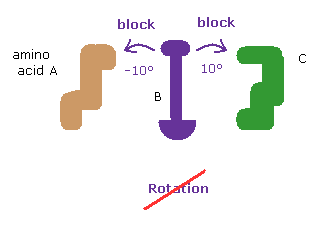
This result shows that the shortest interatomic length is the most important factor to determine each dihedral angle in most cases.
The quantum chemistry and MM methods try to calculate the total potential energy of all atoms to determine conformation.
But this calculation takes extremely much time and it is too complicated to be applied to actual proteins.
And even if potential energy is higher at some configuration, there are cases when the forces are just balanced and cancel each other.
In this case, this configuration can be considered to be stable.
As shown in this page, the collisions of two distant amono acids block these whole rotations and determine the protein structure.
So proteins act like rotating solid body.
(Fig.27) Rotation by 10 degree in the 2nd AK (= 1AKE ).
After rotation back, we choose "second" in the scroll bar, input "10" into the textbox, and click "chain rot" button.
(Fig.28) Rotation by 10 degree at residue 56-CA (= 1AKE ).

As shown in Fig.28, by dihedral angle rotation of all atoms after 56-CA (= atomic number 824 ), some interatomic distances become too short comparing the original shorest length of 3.156 Å in Fig.19.
For example, the distance between nitrogen of GLY (= 675 ) and carbon of LEU (= 935 ) becomes too short (= 2.068 Å )
This means these atoms crash into each other.
(Fig.29) Rotation by -10 degree in the 2nd AK (= 1AKE ).
After returning to the original configuration by clicking "=back" button, input "-10" into the textbox.
And then click "chain rot" button.
(Fig.30) Rotation by -10 degree in the 2nd AK (= 1AKE ).

Also in -10 degree rotation, the shortest interatomic length is 2.721 Å, which is shorter that of the original configuration (= 3.156 Å of Fig.19 ).
From the results of Fig.19 (= original ), Fig.28 (= 10 degree rotation ) and Fig.30 (= -10 degree rotation ), the dihedral angle of 90.8 is the most stable at 56-CA site in the 2nd AK protein.
(Fig.31) Dihedral angles mean most stable positions.

Due to the existence of substrate, the dihedral angles of the first (= 4AKE ) and second (= 1AKE ) proteins are a little different.
In spite of this difference, the common point is that their angles are the most stable positions.
As shown in Fig.22, 25, 28 and 30, when you rotate by ±10 degree from the original angles, some atoms crash into each other in both proteins. And the shortest interatomic distance becomes shorter.
This fact clearly proves that the existence of extremely short interatomic length determines each dihedral angle.
(Fig.32) Adding collision between A and B subunits

Adenylate kinase (=4AKE ) consists of two subunits.
In this this page or above sections, we consider collisions between atoms only inside A subunit.
But actually A and B subunits adjoin each other, and their shortest intersubunit distance is usually about 3.0 Å.
So when we rotate protein chain inside A subunit, these rotated chain in A may crash into B subunit.
In the program above, we can also consider collisions among subunits and HETATM (= other than amino acids ).
(Fig.33) PDB and data file names and saving folder inside program.

Here we use the program below to compute dihedral angles of rotation and crash.
( Pro-2 )
Sample JAVA program ( crash2.java )
(Protein of PDB data file).
AK protein ( open, 4AKE.txt )
20 amino templates ( tout.txt )
As I explain in Fig.9, after saving these data files in some your computer's folder, run the program above.
In this section, we use only the first protein, so the second protein file name is unneccesary ( sfil="", and ffss = 0 ).
The saving folder name in Fig.33 is "C:\sdff". If you save these files in differently named folder, change these parts.
(Fig.34) ±10 degree rotations are blocked in all C, CA sites ?

As I said in Fig.11, ( C, CA ) rotation sites in main chain determine the whole protein structure.
After running the program above, input "0" and press enter key for the first question ( Rotate all angles ? ).
And then input "0" and press enter key, which means only collisions inside A subunit are considered, like in this page.
Fig.34 results show as much as 249 rotation sites are blocked in both ±10 degree rotation (= both-OK ).
On the other hand, only 53 sites are not blocked in one direction. ( these sites are usually near surface. )
This fact clearly proves that the whole protein structure is determined by avoiding every single obstacle in most sites.
(Fig.35) Meaning of resutls.

These meanings are completely the same as this page.
First we find the shortest interatomic length in the original configuration.
If the shortest length becomes shorter by rotation, it means that rotation is blocked = we express it as "OK".
So "both-OK" means ±10 degree rotations are both blocked, "20-OK" means in one direction, 10 degree rotation is blocked, and 20 degree rotation is blocked in another directin.
In cases which are neither "both-OK" nor "20-OK", if we exclude some special short interatomic length ( less than 2.7 Å ), both ±10 degree rotations may be blocked (= "short-OK" ).
In C-site rotation, if ±10 degree rotations are blocked by excluding one N-N length closest to that C site, it means "N-OK".
In cases which are neither of them, if one 20 degree rotation is not block, it is represented as "one-NO"
(Fig.36) Meaning of resutls.
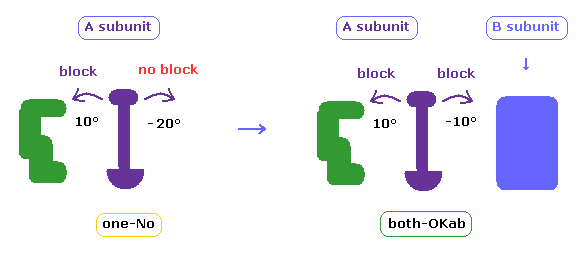
In above section and this page, we consider collisions only inside A subunit.
But 4AKE protein has two subunits (= A, B ) close to each other.
So in some cases, the rotated chain may crash into B subunit atoms (= B subunit acts as an obstacle. ).
In the above program, we can compute these collisions, too.
In cases other than "both-OK", if the rotated chain crashes into B subunit by 10 degree rotation, it is counted as "both-OKab".
( A-B crash means that the shortest interatomic length becomes shorter including A-B ditance by 10 degree rotation, and furthermore its A-B length becomes less than 2.7 Å )
(Fig.37) Considering A-B subunit collision.
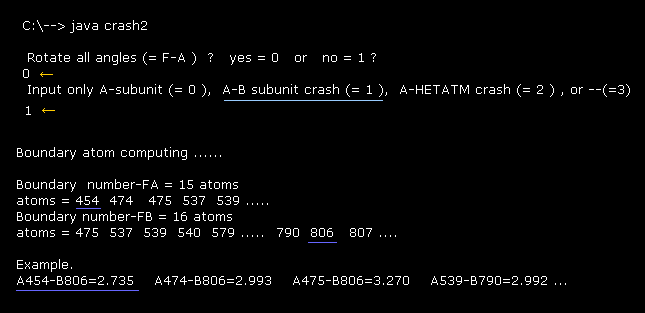
Running above program, input "0" for the first question (= Rotate all angles ? ).
And then input "1" for the second question (= A-B subunit crash ).
"Boundary number" means program atomic numbers, which atoms exist close to the boundary ( < 3.5 Å ) between A and B subunits.
For example, the distance between A subunit atom (= 454 ) and B subunit atom (= 806 ) is 2.735 Å ( < 3.5 Å ), which distance is the shortest between A and B atoms due to repulsive force.
( So extremely short interatomic length is blocked in the original configuration ! )
If we know these atoms in advance, the computing time becomes much shorter, when considering collisions by each rotation.
(Fig.38) Considering A-B subunit collision. → almost all rotations are blocked.

As shown in Fig.38, you can find that almost all ±10 degree rotations are blocked ( both-OK + both-OKab + 20-OK = 358 sites ) in comparison to non-blocked site ( one-No = 35 ).
So collisions among atoms are the most important factor to determine each dihedral angle.
Instead of wasting much time in computing all energy levels in usual quantum methods, we need to concentrate on avoiding every single obstacle due to classical mechanics.
(Fig.39) Considering A-B subunit collision. → almost all rotations are blocked.
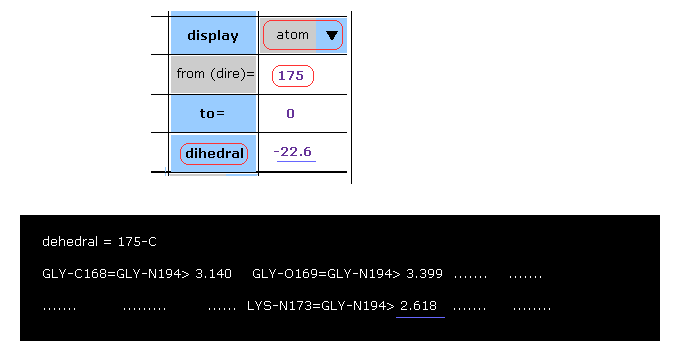
Here we try to confirm these rotations are really blocked, taking C-175 site as an example.
After choosing "atom" in the scroll bar, input program atomic number of "175", click "dihedral" button.
The dihedral angle of 175-C-LYS proves to be -22.6 degree.
In command prompt screen, interatomic distances less than 3.5 Å are shown.
( Between atoms before and after rotation sites within ±20 residues as shown in Fig.32. )
In these distances, you find that 2.618 Å is the shortest.
So if some interactomic distance, which is shorter than this 2.618 Å, appears by some rotation, this means this rotation is blocked, and the original configuration is more stable in balance.
(Fig.40) 10 degree rotation at 175-C site → blocked.
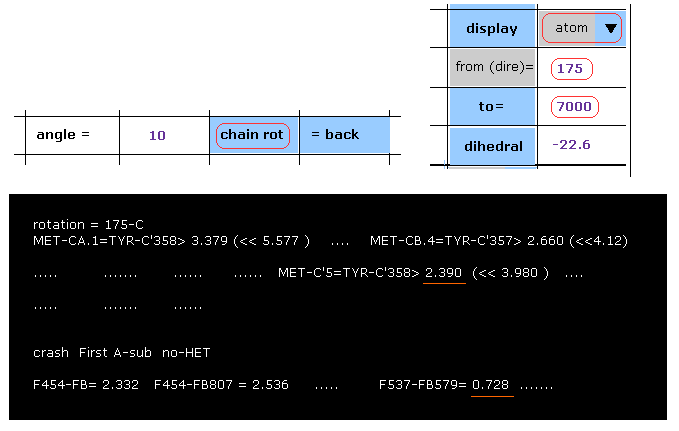
When you want to rotate all atoms after 175-carbon, input "175" and "7000" (= arbitrary value greater than final atomic number "3355" ) into the designated textboxes, and then click "chain rot" button.
As shown in Fig.40, the distance between carbon-5 of MET and carobon-358 of TYR becomes shorter (= 2.390 Å ) than above 2.618 Å by this 10 degree rotation.
This means 10 degree rotation at this site is blocked (= "OK" ).
In the section of "crash First A-sub", interatomic distances less than 2.8 Å between A and B subunits are shown.
For example, the distance between subunit A atom-537 and subunit B atom 579 becomes extremely shorter (= 0.728 Å ), which means "crash".
The shortest A-B distance in the original configuration is 2.735 Å, as shown in Fig.37.
(Fig.41) -10 degree rotation at 175-C site → blocked.
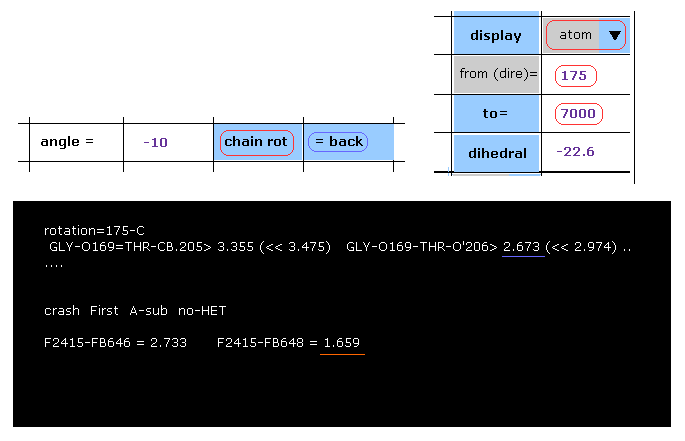
Then click "=back" button to return to the original configuration, and then input "-10", click "chain rot" button.
As shown in Fig.41, the shortest interatomic distance is 2.673 Å, which is still longer than that of the original configuration (= 2.618 Å ).
But when you see "crash" section below, you find that the distance between subunit A atom 2415 and subunit B atom 648 becomes extremely shorter (= 1.659 Å ), which is less than 2.618 Å.
This program express this site as "-10-OKAB", which is counted as "both-OKab".
Of course, as you see, this rotation is clearly blocked.
(Fig.42) Collisions with substrate (= HETATM ).
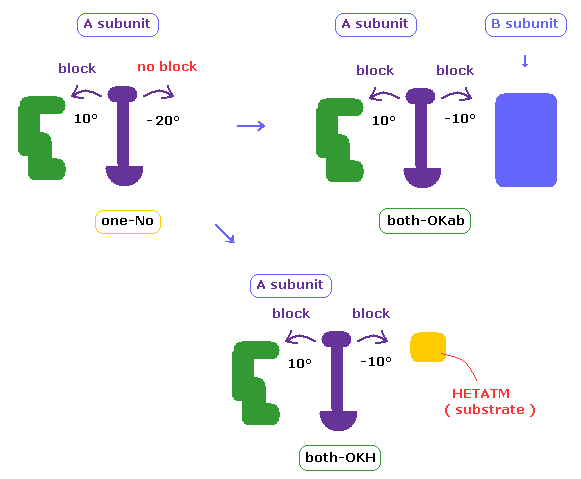
1AKE is the closed typer of AK protein, which has substrate as HETATM atoms.
( 4AKE also has HETATM atoms, but they are all H2O, which is not considered in this program ).
Using the sample program below, we investigate collisions are blocked by the existence of substrate.
( Pro-3 )
Sample JAVA program ( crash3.java )
(Protein of PDB data file).
AK protein ( closed, 1AKE.txt )
20 amino templates ( tout.txt )
(Fig.43) PDB and data file name and saving folder.

Instead of "crash3.java", you can use "crash2.java" of Pro-2, after changing PDB file name ( 4AKE → 1AKE ).
(Fig.44) Almost all rotations are blocked also in 1AKE protein

First we consider only collisions inside A subunit ( not A-B, not A-HETATM ).
After running the program above, input "0", and "0" like Fig.34.
The results show the number of ±10 degree rotation blocked sites (= 260 ) is much larger than one-No blocked site (= 62 ).
As shown in Fig.12, almost all corresponding dihedral angles are changed between 4AKE (= open ) and 1AKE (= closed ) proteins due to the existance of substrate. ( Their angle diffrences are about 10 - 20 degree. )
But comparing Fig.34 and Fig.44, you find ±10 degree rotations are blocked in almost same numbers of sites in them.
This fact proves that protein configuration is changed and determined by avoiding every single obstacle, even after binding some substrate.
(Fig.45) A-B subunits collisions are considered.

After running the program, if you input "0" and then "1" (= A-B subunit crash ), Collisions between A and B subunits are also considered like Fig.38.
As shown in Fig.45, the number of total rotation-blocked sites (= both-OK + both-OKab + 20-OK = 354 ) are much larger than one-No sites (= 40 ).
So as I said, avoiding extremely short interatomic length is the most important factor in protein configulation.
(Fig.46) A and HETATM (= substrate ) collisions are considered.

1AKE protein has substrate (= HETATM ).
If you input "0" and then "2" (= A-HETATM crash ), collisions between A subunit and substrate are also considered.
This substrate is very close to A subunit, so as much as 48 atoms in A subunit are within 3.5 Å from substrate.
Almost all distances between A subunit and the substrate are 2.7 - 3.5 Å.
Only two parts (= 2.002 Å, 2.229 Å ) are too short, because in this site, the substrate is covalently bound to A subunit.
As shown in Fig.46, you find almost all ±10 degree rotations are blocked ( both-OK + both-OKH + 20-OK = 380 ) in comparison to "one-No" sites (= 23 ).
So small molecules or metallic ions which are in contact with proteins are very powerful factor to determine protein configuration.
Next we investigate about 2PAH.txt -- hydroxylase protein.
Save this PDB data files, and change the file name of "1" part into "2PAH.txt" in Fig.43 inside crash3.java .
(Fig.47) Rotations in 2PAH.
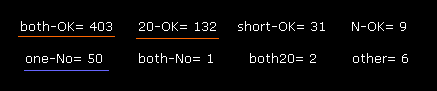
Fig.47 is the result of dihedral angle rotation and collisions only inside A subunit.
( After running the program, input "0" and "0". )
You understand that almost all sites (= 403 + 132 = 535 ) are blocked in ±10 degree rotations.
(Fig.48) Rotations in 2PAH (including A-B crash ).
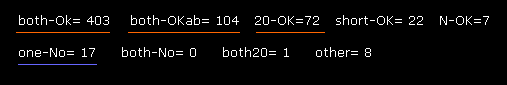
If you input "0" and then "1" (= A-B subunit crash ) after running the program, you will be convinced that almost all sites are blocked in ±10 degree rotations.
Blocked sites ( both-OK + both-OKab + 20-OK = 577 ) vs. one-No sites (= 17 ).
2J96.txt 2ISY.txt
2J0X.txt 2IU4.txt
1CTS.txt 1ROP.txt
Try various other PDB files.
Almost all manipulations are the same as this page.
If you click "ang colo" button once, atoms inside A subunit turns red, and B subunit becomes green ( in both 1st and 2sd proteins. )
And if you click it one more, 1st protein becomes red, and 2nd protein becomes green.
( And if click one more, return to the original color. )
(M-1) Change "select" atom.

If you change "select" atom, choose "first" or "seond" in the scrollbar, input program atomic number ( ex. 1000 ), and then click "select" button.
In M-1 case, we choose atom-1000 in the second protein.
If you want to choose atoms inside B, C, or D subunits, add "10000", "20000", or "30000" to the atomic number.
( For example, "11000" means atom-1000 inside B subunit. )
Also in case of "to=" and "dislay" buttons, after choosing "first" or "second", do the same manipulations as this page.
(M-2) Which moves ?
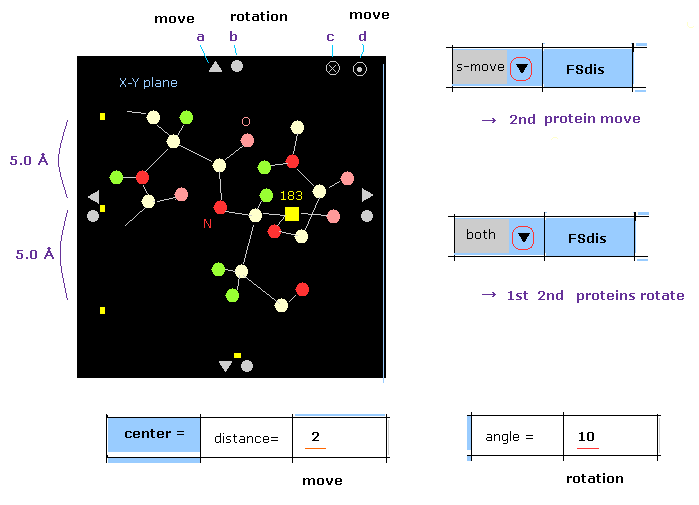
Basically, if you click some triangle mark (= a ), both 1st and 2nd proteins move in that direction.
When you click this mark, after choosing "f-move" or "s-move" in the scroll-bar, only 1st or 2nd protein moves.
( If the inputted value ( next to "distance=" ) is greater than 20, the moving distance becomes "2 Å". )
In case of rotation, basically only 1st or 2nd protein rotate, when you click some circle mark (= b ) for saving time.
When you click that mark after choosing "both", 1st and 2nd proteins are both rotated by the designated angle.
(M-3) changing boundary atoms.
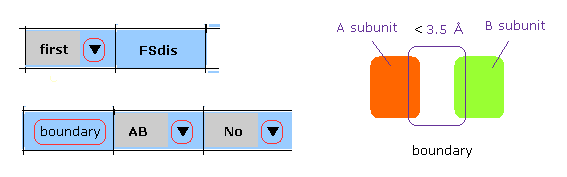
In M-3, after choosing "first", "AB" and "No" in each scroll bar, we click "boundary" button.
In this case, atoms which are close to A-B subunit boundary ( < 3.5 Å ) inside the first protein are shown in command prompt screen.
And after that, when you use "chain rot" button, these collisions are considered.
(M-4) A subunit-HETATM boundary.
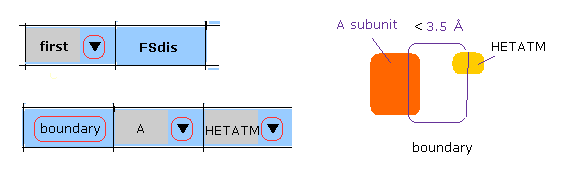
When you click "boundary" button, after choosing "A" and "HETATM", "A" subunit atoms inside the first protein, which is close to HEATM ( < 3.5 Å, excluding H2O ), are shown in command prompt screen.
And after that, when you use "chain rot" botton, A-HETATM crash is considered.
(M-5) 1st and 2nd protein boundary.
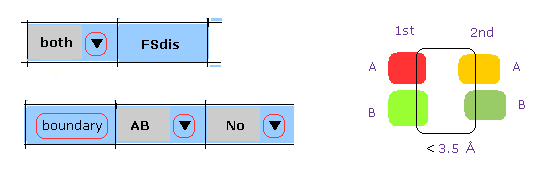
When you click "boundary" button, after choosing "both", "AB", and "No", 1st and 2nd protein atoms, which are close (< 3.5 Å ) to the boundary between 1st and 2nd proteins, are shown in command prompt screen.
Basically "No" means "HETATM crash" is excluded.
If you choose "AB" and "AB" instead of "AB" and "No", this program consider all boundary (AB and AB), (AB and HETATM ), so it takes more time to compute.
If you click "FStext" button, textbox and particle screen are changed between the first and the second proteins.
Of course, if there is only one protein (= only first protein ), this button is meaningless.
If you click "FSdis" button, the second protein disappears.
And if you click it one more, the first protein disappears, and the second appears.
And if you click it one more, both proteins appear (= original state ).
Of course, if there is only one protein (= only first protein ), this button is meaningless.

2013/10/16 updated. Feel free to link to this site.