トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは実在しない
我々の新しいボーア模型によって、ヘリウム原子の基底状態エネルギーの計算で、量子力学的な変分法よりも正確な結果をだすのに成功した。(トップページ参照のこと)。
この成功した新ボーア模型では、ヘリウム原子 (He) の2つの電子は、ちょうど1ド・ブロイ波長の互いに垂直な軌道上を運動している。
また、この新しい原子模型は、パウリの排他原理の現象も正確に説明できる。なぜなら、この新しいボーアの2電子原子には、3つめの電子が入りこむスペースがないからだ。
驚くべきことに、この新しいボーアのヘリウム構造は、他の原子(イオン)である、リチウム原子 (Li) や 炭素原子 (C) にもあてはめることができた。
(例えば、ボーアのリチウムページも参照のこと。)
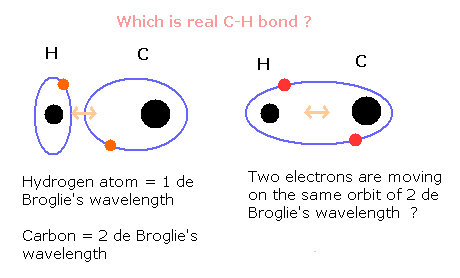
メタン (methane) は、化学式 (CH4) の化合物である。
それは、”正四面体”の構造のため、無色、無臭、無極性である。(結合角は、109.5°である。)
一般の量子化学によると、メタンの C-H 結合においては、2s と 2p 軌道の代わりに sp3 混成軌道が形成されなければならないとしている。
しかし、量子力学には、この化学結合に関して、より具体的かつ詳細な構造を説明する力はない。
なぜなら、量子力学(化学)は、”本当の”物理的イメージを表現することができないからだ。
(それは、単に”数学的な”模型を示すだけである。(このページも参照のこと。))
ボーア模型は、シュレディンガー方程式と同じように、水素原子を正確に表現することができる。
(また、ボーア・ゾンマーフェルト模型はディラック方程式と同様に水素原子の相対論的効果を正確に表すことができた。このページも参照のこと。)
さらに、炭素原子においても、ボーア模型による方法で近似的な軌道を計算することができた。
炭素模型においては、炭素原子の4つの価電子は、核の周囲に正四面体状に配置されている。
(このページも参照のこと。)
そこで、ここでは、この新しいボーア模型を使って、メタン分子 (CH4) の”本当の”電子の運動を追求することにする。
メタン分子では、1つのC-H 結合を切断するのに、435 kJ/mol が必要である。
しかし、4つすべての C-H 結合を切断するには、1663 kl/mol ( = 17.235 eV ) が必要である。
つまり、平均の結合エネルギーは、 1663/4 = 416 kJ/mol となり、これは、435 kJ/mol とは等しくはない。
結果として、メタン (4つの炭素の価電子+4つの水素原子) の基底状態のエネルギーは、-148.024 -54.416 -17.235 = 219.675 eV となる。
中性の炭素は6つの電子をもち、(2 × 1S 電子 + 4× 価電子) 2つの 1S 電子は核にとても近づいている。
つまり、近似的に4つの電子が +4e の中心核 (+6e-2e = +4e) の周囲を運動していると仮定できる。
重要な点は、水素原子と炭素原子の電子の間の関係である。
もともと、水素原子は、1ド・ブロイ波長の1軌道を有している。
一方で、炭素原子の外殻電子は、2ド・ブロイ波長の軌道を運動している。
(この事実は、炭素イオン (C3+) のエネルギー計算によって確かめられている。ボーアの炭素も参照のこと。)
それでは C-H 結合が形成されたとき、これら2つの軌道がどのように変化するのだろうか?
水素原子は、1ド・ブロイ波長の軌道を維持できるのだろうか?
それとも、水素と炭素の外殻電子2つで、1つの2ド・ブロイ波長の混成軌道を形成するのだろうか?
Fig. 1. メタン (CH4) の C-H 結合の真の姿は ?

この質問に答えるために、次のサンプル JAVA プログラムを使って、微小時間ごとに粒子間のクーロン力を計算し、メタンの電子の運動を調べることにする。
サンプル JAVA プログラム (CH4)
メタンは分子であり、水素原子と炭素原子がゆるやかにつながっている。
そして、それらの原子は、ある程度は独立に振動している。
さらに、炭素原子は7体問題 (6電子+1核)である。
つまり実際には、これらの電子は、(歳差運動もふくめて)かなり複雑に運動している。
このプログラムを使って、我々は、メタンの”近似的な”電子軌道を知ることを目標とする。
まず最初に、水素原子の電子軌道 (1ド・ブロイ波長) と、炭素原子の電子軌道 (2ド・ブロイ波長)が、Fig. 2のように分離していると仮定する。
Fig. 2. 推定されるメタン (CH4) の”本当の”構造。
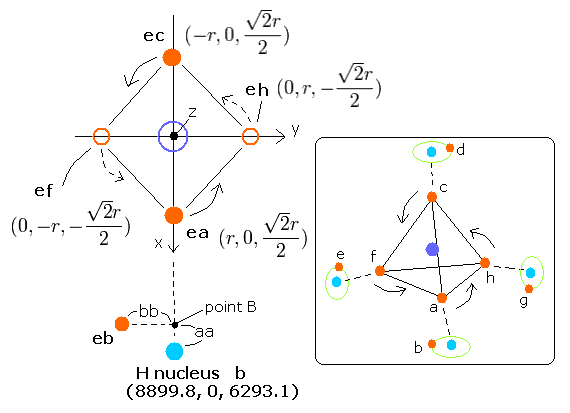
このプログラムでは、炭素原子核(これは +4e = +6e-2e と仮定している)が原点に位置し、4つの水素原子核は”正四面体”状に配置されている。
C-H 結合の平均結合距離は、1.09 × 10-10 meter (=10900 MM) である。
計算のため、次の新しい単位を使っている。
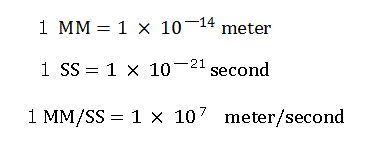
ここでは、水素原子核を次の座標に固定している。 (in MM);
Hydrogen b nucleus --- (hbx, hby, hbz) = (8899.8, 0, 6293.1)
Hydrogen d nucleus --- (hdx, hdy, hdz) = (-8899.8, 0, 6293.1)
Hydrogen e nucleus --- (hex, hey, hez) = (0, -8899.8, -6293.1)
Hydrogen g nucleus --- (hgx, hgy, hgz) = (0, 8899.8, -6293.1)
このサンプルプログラムでは、実行すると、まず、電子a (ea) の最初のx座標 r (MM) を入力するように画面に表示される。
電子b(水素原子の)に関しては、最初の座標 aa と bb (in MM) を入力する。
aa は 水素原子核 b と point B (=電子 b の座標を 炭素原子核と水素原子核 b を結ぶ線に投影した交点) の間の距離。
(aa が負の値のとき、この point B と 原点は 水素原子核 b を挟んで互いに逆に位置する。)
bb は、この point B と 電子 b の間の距離。(この bb が正の値のとき、電子 b のy座標は、負になる。)
この入力値から、炭素原子の4つの外殻軌道の電子 (ea, ec, ef,eh) と、4つの水素原子の電子 (eb, ed, ee, eg) が正四面体状に配置される。
電子a が 自身の1.0, 1.9, 2.0 ド・ブロイ波長分の軌道を進み、かつ、電子 b が 1ド・ブロイ波長分の軌道を進んだとき、このプログラムは次の値を画面に表示する。
各電子の位置座標、
最初と最後の地点における炭素(もしくは水素)原子核と 電子a(もしくは電子b) の距離、
また、電子a の軌道上の点の中で、最も核との距離が長く(もしくは短く)なるときの、その距離。
おそらく、最初の速度ベクトルの方向は、歳差運動のため、ゆっくりと変化していると思われる。
しかし、それを考慮するととても大変なため、ここでは最初の速度ベクトルを次のように固定する。
電子 a の速度ベクトルの各成分の比 = ( 0, 8, -1 )
電子 b の速度ベクトルの各成分の比 = ( 0, 0, vb )
電子 a の最初の x 座標 (r) が 5500 MM (= 0.5500 × 10-10 meter) で、かつ aa と bb の初期の値が、それぞれ -700 と 3750 のとき、すべての電子 が、ea 軌道に含まれるド・ブロイ波長の数が 1.9 ˜ 2.0 になったとき、おおよそ最初の状態に戻ってくることができる。(少し歳差運動を伴って。)
電子 a と、核の間の初期の距離は 6736 MM で、その最後の距離は 6535 MM である。
電子 a の最初のy座標は 0 MM で、その最後のy座標は 422 MM ˜ 2328 MM である。
核と電子軌道上の点との間の距離で、最も長くなる時は、7169 MM (= おおよそ最初の距離)で、 最も短くなるときは 4805 MM である。
電子 b (eb) に関しては、wa が 2.0 になったとき、eb の軌道に含まれるド・ブロイ波長の数は、ほぼ 1 になる。
電子 b と水素原子核 b との間の最初の距離は、3814 MM で、最後の距離は 3588 MM となる。
電子 b の最初のy座標は -3750 MM, 最後のy座標は、 -2286 MM ˜ -1269 MM になる。
もし、電子 a と電子 b が、2ド・ブロイ波長のほぼ同じ軌道 を運動していると仮定して、プログラムを実行すると、電子 b は、炭素原子核に到達することはできない。なぜなら炭素原子核には、電子 b を炭素原子核の周囲の軌道を運動させるほどの引力はないからだ。
この結果は、Fig. 1 において、水素原子が炭素の軌道とは別の、1ド・ブロイ波長の軌道を維持することを示している。
H2O のビリアル定理も参照のこと。
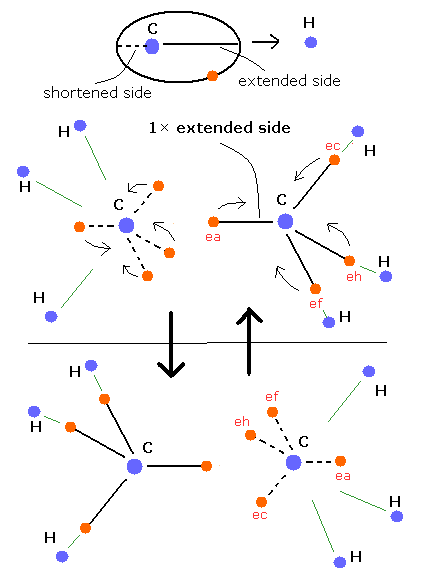
上のメタンのセクションに見られるように、他の原子の正の原子核があるとき、炭素の電子軌道は、この他の原子の側ではクーロン引力のため Fig. 3 のように引き伸ばされる (extended)。
(他の原子のある反対側では、炭素の電子軌道は短くなる傾向がある。)
Fig. 3. 推定されるエタン (CH3-CH3) 模型
エタン (CH3-CH3) の C-C 結合長は、約 1.54 × 10-10 meter (=15400 MM) である。
上のメタンの数値 (炭素原子核と電子 a の間の最も長い距離) は、7169 MM であり、これは、C-C 結合の約半分である。( 15400/2 = 7700 MM )
つまり、H と C は別のものだが、この計算値はおおよそ妥当な値といえる。
通常の化学によると、単結合がエタンの2つの炭素原子間に形成されるといわれている。
ところで、この単結合とは一体全体何なんだろうか??
この新しいボーア模型の視点からすると、C-C 単結合とは、Fig. 3 に示されるように2つの炭素原子核間に1つの引き伸ばされた炭素電子軌道の存在で説明することができる。
炭素の電子は、周期的に核の周囲を運動している。つまり、”引き伸ばされた (extended)”側と”短くなった (shortened)”側の軌道を行き来している。
エタンは、6つの正の水素原子核が存在している。そのため引き伸ばされた電子軌道は、同時にはたった一つしか2つの炭素原子核間に存在することができない (Fig 3.)。
(一方で、電子間のクーロン反発力のため、2つの炭素原子核間では、一つの側の軌道が引き伸ばされているときもう片方の軌道は短くなっている。)
引き伸ばされた軌道上の電子は、短い軌道上のものより、他の炭素原子核に近い。
そのため、2つの炭素原子核間に、より多くの”引き伸ばされた”電子軌道が存在するほど、炭素原子核間の結合力は強くなる。
エタン (CH3-CH3) では、”ねじれ型配座 (staggered conformation)”が、”重なり型 (eclipsed conformation)”よりも少し安定している。
しかし、どうしてこのねじれ型がより安定しているのかはまだ論争中である。
これのは2つの仮説がある。
もし、ねじれ型になると、2つの炭素に属する水素原子間の距離が遠くなる。
そのため、一つめの説としては、C-H 結合の電子対の距離が遠くなるため、反発力が弱くなりより安定するというものだ。
(しかし、一方で、水素原子核と電子対の距離も離れてしまい、クーロン引力の減弱により不安定にはならないのか? とも言える。)
もう一つの説としては、1つの炭素上の C-H結合性軌道と隣の炭素上の C-H反結合性軌道間の相互作用でねじれ型が安定するというものである。
どちらの場合も、違う炭素原子に属する水素原子間の距離は、C-C 結合長に比べてかなり長い。
そこで、ここでは新しいボーアのエタン模型を使用して、この理由を探究してみることにする。
Fig. 4. エタンにおける、"ねじれ型 (Staggered)" と "重なり型 (Eclipsed)" 配座.
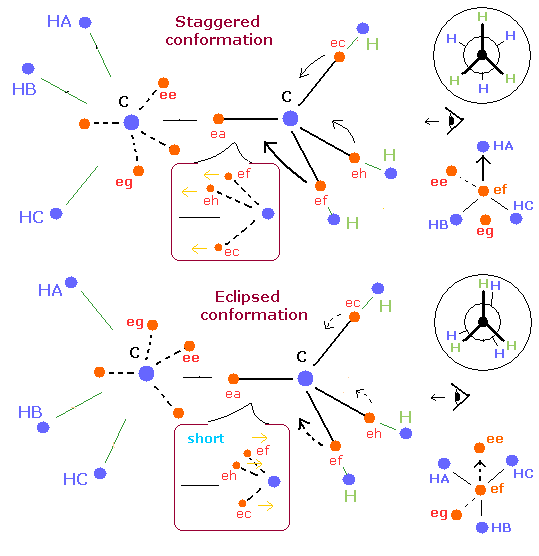
Fig. 4 は 新しいボーア模型と Newman 投影式を使って、エタンの”ねじれ型”と”重なり型”を示している。
ここでは、一つの電子 (ef) に注目する。
”ねじれ型”では、一方の炭素の各水素原子核は、他方の炭素の各電子の進行方向の地点に配置されている。
( ef → HA, eh → HB, ec → HC )。
つまり、”ねじれ型”では、電子 ef は、水素原子核 (HA) の方向に向かっている。
(また、電子 eh は、水素 HB の方向へ向かっている。)
一方、”重なり型”では、電子 (ef) は、水素の方向へ向かっていない。
むしろ、水素原子核 (HB) から遠ざかっている。
つまり、”重なり型”では、C-C 原子核間の各電子軌道は、”ねじれ型”よりも短くなる。 (水素原子核の引力に逆らって動くため。)
結果として、C-C 原子核間のこれらの短くなった軌道は、エタンの結合状態をより不安定にしてしまう。
(異なる炭素の水素原子間の距離はかなり離れているため、比較的に上記の C-C 間の状態違いによる影響は、大きいと考えられる。)
6つの水素原子を持つエタンの場合は、Fig. 3 にしめすように、2つの炭素原子核間にはたった1つの引き伸ばされた側しか同時には存在できない。
エチレン (CH2=CH2) の場合はどうだろうか?
エチレンには、4つの水素原子があり、それらは同一平面上 (x-z 平面) に配置されている。
この新しいボーア模型を使うと、Fig. 5 に示すようにエチレンを正確に表現することができる。
Fig. 5. 推定されるエチレン (CH2=CH2) 模型。
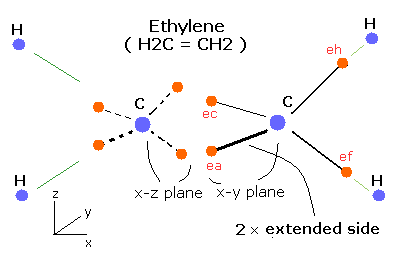
Fig. 5 に示すように、C=C 結合間では、2つの引き伸ばされた軌道 (extended side) が同時に存在することができ、これは、エタンのC-C 結合よりも結合エネルギーが大きくなる原因となる。
また、2つの炭素原子間の間の4つの電子は、互いに反発しあっている。
(Fig. 5 に示すように、それらのうちの2つは、x-z 平面、他の2つの電子は、x-y 平面に位置する。)
同様に、Fig. 6.のようにこのボーア模型を使って、アセチレン (HC ≡ CH) を表現することができる。
Fig. 6. 推定されるアセチレン (CH ≡ CH) 模型。
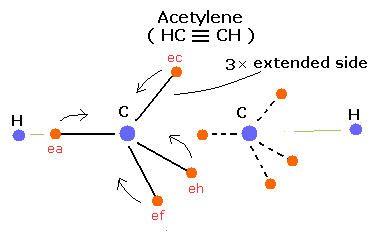
アセチレンは、たった2つしか水素原子を持たない。そのため、炭素の電子は2つの炭素原子核間に集まる傾向にある。
(この場合では、C ≡ C 結合間に 3つの引き伸ばされた軌道が存在することができる。そのため、結合エネルギーはより大きくなる。)
C=C 結合と C ≡ C 結合では、”正四面体”の構造が少し崩れる と考えられる。なぜなら、2つもしくは3つの電子が他の炭素の1つの原子核にひきつけられるからである。
そのため、エタンはエチレンやアセチレンに比べて、より対称的な構造を有しているといえる。
これが、エチレンとアセチレンが、結合エネルギーが大きいにも関わらず、より反応しやすい理由である。
例えば、エチレンの C=C 結合では、H-C-H の角度は、117.4° である。(109.5°ではない。)
Fig. 7. エチレン (CH2=CH2) の C=C 結合。
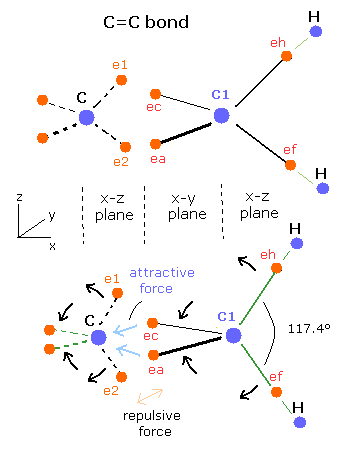
Fig. 7 に示すように、C=C 結合では、2つの電子 (ea,ec) の”引き伸ばされた”軌道が、1つの炭素原子核 (C) に引き寄せられる。
つまり、もう一方の側の2つの電子 (e1, e2) は、電子間のクーロン反発力ではじかれ、その結果少しだけ、正四面体の構造が崩れる。
結果として、 ( eh-C1-ec ) と ( ef-C1-ea ) の角度が、109.5°よりも大きくなる。平衡状態を保つために、(eh-C1-ef) の角度も 109.5°よりも大きくなる。
残念ながら、量子力学には、我々のボーア模型のように具体的なイメージで説明する力はない。
例えば、両方の炭素に属する C-H 結合の電子間の反発力をどう説明するのだろうか?
(もし、これを考慮したら、エタンのセクションの”ねじれ型”配座のように、4つの水素原子は同一平面上にのれないのではないか?)
また、π 結合の電子と、C-H 結合の電子との間の反発力についてはどうするのだろうか?
それに、1つの炭素に属する、C-H 結合の電子間(もしくは、2つの水素原子核間)の反発力を考慮すれば、H-C-H の角度は、120°よりも大きくならなければならないのでは?
最も重要な点は、結合エネルギーは、電子が他の電子を避けながら、他の正の原子核に引きつけられることによって生じる。
もし、反発力よりも、クーロン引力が強いときに、”安定な”結合状態が形成される。
(クーロン引力と反発力によって生じるエネルギー差が”結合エネルギー”である。)
しかし、普通の教科書には、C=C 結合の π と σ 結合は、同じ平面上にのっている。
(普通の量子化学によれば、π と σ 結合が x-y 平面 にあるとき、すべての C-H 結合は、x-z 平面にのっている。)
なるべく他の電子を避けながら、他の炭素原子核に近づくには、C=C 結合の4つの電子は、我々のボーア模型のように 異なった平面に配置されるのが普通である。

2010/8/23 updated This site is link free.