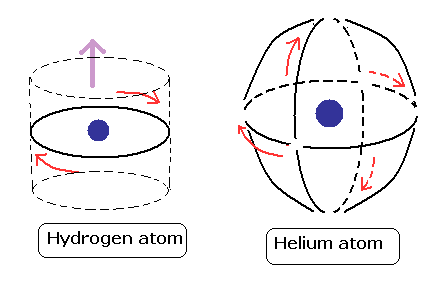
コンピューターを使った方法では、これらの軌道の長さはちょうど1ド・ブロイ波長だということがわかった。
パウリの排他原理によれば、リチウムの三番目の電子は、1s軌道に入ることができない。
この図に示すように、ボーア模型のヘリウムには、3番目の電子が入る余地はもう残っていない。なぜなら、2つの電子軌道がちょうど垂直に交わっているからだ。
また、ボーア模型はとても”奇妙な”電子のスピンのさまざまな問題を解決することができる。(このページを参照のこと!)
トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは現実には存在しない。 単なる数学上の産物
ボーア模型により量子力学的変分法は説明可能である。
ヘリウム(He)、ネオン(Ne)、アルゴン(Ar)などの希ガスは、無色、無臭、で不活性な原子である。
そのため、それらの原子構造(電子配置)は対称的で無極性のように思える。
しかし、単に”対称的な”原子構造だけでは、化学的に不活性の性質を十分には説明できない。
例えば、水素分子(H2)やメタン(CH4)なども、対称的な原子構造のため、無色、無臭、無極性である。
また、これらの気体の沸点、融点も低い。
しかし、それらは、大変に燃焼しやすい。(実際、酸素などと爆発的に反応する。)
このことは、周期表における希ガス(18族元素)の不活性の性質を説明するには、対称的な特性以外のものも必要であることを意味する。
(もちろん、対称的な電子配置も不可欠なことはいうまでもない。なぜなら、もし外殻の電子が不均等に分布していると、負電荷の電子の殻に”すきま”を生じてしまう。
原子全体の電荷はゼロである。なぜなら、原子核の正電荷の大きさとすべての電子の負電荷の大きさがちょうど同じだからである。
つまり、原子核の正電荷の効果を打ち消すには、同じ大きさの負電荷の電子群が、ちょうど、均等に核の周囲に分布していなければならない。
そうしないと、原子核の正電荷の影響が外部に漏れてしまい、このことにより、他の原子と反応する確率を高くしてしまう。)
標準的な量子化学によれば、外殻が価電子によっていっぱいになることが、希ガスの不活性化の原因だとしている。
しかし、量子化学(量子力学)は、これ以上の具体的な理由については何も教えてくれない。
1920年代に、ボーア模型は3体問題であるヘリウム原子の基底状態のイオン化エネルギーに関しては説明することはできなかった。
一方で、1929年、ヒレラスがシュレディンガー方程式を使った変分法でその近似値の計算に成功し、時代は量子力学へと進む転換点となった。
しかし、最近、我々は、簡単なコンピュータープログラムを使った方法で、ボーア模型によるヘリウムの基底状態のエネルギーの精密な計算に完全に成功した。
トップページ (2電子原子も含む正確な新ボーア模型)をぜひ見てほしい!
現在、とても複雑な変分法によって、量子化学者たちは、ヘリウムのエネルギー計算に成功したと主張している。
しかし、そこには、いくつかの問題点があることは否めない。
第一に、1000 以上の複雑な基底関数の”羅列”が、”真の”ヘリウム原子の構造を表現しているとはとても言い難い。(想像すらできない。)
第二に、ヘリウムの基底状態のエネルギー(イオン化エネルギーの合計)の最新の実験値は、Nistによれば、-79.005146 eV ( = 2.903385428 Eh ) である。
しかし、これらの変分法の計算結果はこの正確な実験値とは少し異なるのだ。
なぜなら、シュレディンガー方程式は明確な電子軌道なるものをもたないため、核の運動を正確に計算することができないからだ。
(三体問題であるヘリウム原子では、シュレディンガー方程式は、”いつ”2つの電子の中心が核の位置と一致しているか判断できないからだ。)
三番目に、シュレディンガー方程式では、最も安定なヘリウム原子の”基底状態”の電子でさえ、核から無限遠近く離れたところの確率密度がゼロにならないのだ。
また、電子と核の距離が、ある程度離れたところだと、クーロンポテンシャルエネルギーが、原子の全エネルギーよりも高くなる。
これは深刻な問題を引き起こす。なぜなら、これらの地点では、何と運動エネルギーがマイナスになってしまうからだ! ( 1/2 mv2 < 0 )
こんな馬鹿げたことが本当にあるのだろうか?
(あなたは、実際にこのマイナスの運動エネルギー状態を想像できるだろうか?)
次に、ヘリウム原子の基底状態の計算をした研究結果を表示する [6]。
| Author | Number of basis function | Calculation results (Eh) |
|---|---|---|
| Godman, 1998 [2] | 8066 | -2.903724377034119594 |
| Chuluunbaatar et al. 2001 [3] | 5669 | -2.90372437703411959829 |
| Sims and Hangstrom [4] | 4648 | -2.9037243770341195982999 |
| Drake et al. 2002 [5] | 2358 | -2.903724377034119598305 |
| Vladimir I. Korobov 2002 [6] | 5200 | -2.903724377034119598311159 |
| extrap | --- | -2.903724377034119598311 |
この表に示すように、シュレディンガー方程式を使った変分法では、-2.903724377034119598311 ( = -79.014347... eV )より正確な計算結果をだすことはできない。( 正確な実験値は-79.005147 eV である。)
なぜなら、これらの方法は、核の運動を正確に計算することができないからだ。( > +0.011eV )
ヘリウム原子の電子の速度はヘリウムイオン( He+ )よりも遅く、水素原子よりも速い。
つまり、相対論的なエネルギーの補正値は、He+ ( -0.0028 eV ) と水素原子 ( -0.000.. eV ) の間にあることになる。
我々のボーア模型による方法では、変分法によるこみいったやり方よりも正確な結果をだすことに成功した。( -79.0035 eV の計算値をだすことに成功した。つまり、相対論的なエネルギーの補正値は -0.001647 eV ということになる。)
さらに、2つの対称的な軌道が垂直に交わっているという原子模型は、ヘリウムの安定性と閉殻性を説明することができる。
(トップページ を参照のこと。)

コンピューターを使った方法では、これらの軌道の長さはちょうど1ド・ブロイ波長だということがわかった。
パウリの排他原理によれば、リチウムの三番目の電子は、1s軌道に入ることができない。
この図に示すように、ボーア模型のヘリウムには、3番目の電子が入る余地はもう残っていない。なぜなら、2つの電子軌道がちょうど垂直に交わっているからだ。
また、ボーア模型はとても”奇妙な”電子のスピンのさまざまな問題を解決することができる。(このページを参照のこと!)
標準的なヘリウム模型では、1s軌道の2つの電子は、ゼロの角運動量をもっていることになっている。
しかし、もしそうだとしたら、ヘリウムの2つの電子は、毎回、核に衝突するたびに、跳ね返ったり(もしくは、貫いたり !?)しているのだろうか?
これは、非常に不安定なヘリウム模型と言わざるをえない!
また、標準的なヘリウム模型は、スピンアップとスピンダウンの電子を持っており、磁場を生じないことになっているが、正確にいえば、この2つの電子はクーロン反発力で空間的に離れており、ほぼほとんどの地点で磁場はゼロにならないことになってしまう。
つまり、量子力学のヘリウム模型は自己矛盾を含んでいることになる。
メタン(CH4)に見られるように、単に原子構造が対称的で無極性であることは、強い安定性を意味しない。
ヘリウム原子は単に2つの電子をもった原子とは違うのである。
この安定性を説明するには、原子には他の理由が必要となる。
なぜ 孤独なヘリウムには化合物がないのか? も参照のこと。
上の図に示すように、ボーア模型の2つの電子は安定した、ド・ブロイの(ちょうど1波長の)振動波の殻の中を周期的に運動している。
また、厳密な計算結果は、実際にこのド・ブロイ波の存在を示唆している。
ネオン(Ne)やアルゴン(Ar)では、外殻のsとp軌道のすべてが電子でいっぱいになっていると言われている。
(原子番号はそれぞれ、10(Ne)と18(Ar)である。つまり、この2つとも価電子の数がちょうど8である。)
しかし、このsとp軌道の形というのは、実際に実験で確かめられない。単に理論上のものである。
アンモニア(NH3)やメタン(CH4)などの分子では、1つの2s軌道と3つの2p軌道が混ざって4つのsp3混成軌道になる。
また、NH3では、4つめのsp3軌道には窒素(N)の共有結合してない2つの電子(非共有電子対)が入っている。
これらの正四面体形の電子配置はとても道理にかなっており、また実験で確認することができる。(これはすなわちこれが”実在する”配置だということを示している。)
ここに一つ質問がある。
このNH3の非共有の電子対はもともと、正四面体状の一角に配置されていた可能性はないだろうか?
(つまり、想像上の2sと2p軌道などの代わりに、sp3軌道がもともと存在していたという可能性はないだろうか? (特にNeやArなどの希ガスにおいて))
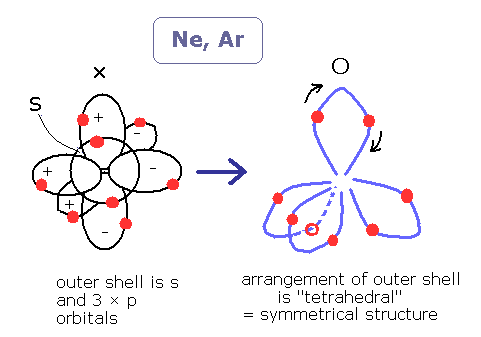
NeやArなどの希ガスでは、価原子の数はちょうど8である。
つまり、これらの8つの価電子(4つの電子対)は、”ほぼ楕円形の”軌道上を運動していて、かつ、正四面体状に配置されていると考えるのがきわめて自然である。
(正四面体が2つ重なると正六面体になる。ボーアのネオン (Ne) も参照のこと。ネオンの構造は若干複雑である。)
この構造はちょうど、クーロン力の条件とも合致している。
(NeやArでは、外殻の電子軌道がド・ブロイ波の2倍かそれ以上のため、軌道の形が多様化でき、8つの電子が入るスペースがあると考えられる。ここがヘリウムと違うところだ。)
前に言ったように、希ガスの不活性を説明するには、我々はクーロン力以外の何か”別の”力を使う必要がある。
希ガスにおいては、安定した対称的な ド・ブロイ波の振動波(これは”整数倍”のド・ブロイ波長を意味する。)が原子全体をきれいに包んでいると考えられる。
また、価電子の数(He=2、Ne,Ar=8)とクーロン力を考慮すると、上の原子構造等はとても自然といえる。
[1] E.A. Hylleraas, Z. Physik 54, 347 (1929).
[2] S.P. Gordman, Phys.Rev.A 57 R677 (1998).
[3] O. Chuluunbaatar, I.V. Puzynin, and S.I. Vinitsky, J.Phys.B: At, Mol.Opt.Phys.34,L425 (2001).
[4] J.S. Dims and S.A. Hagstrom, Int. J. Quantum Chem.
[5] G.W.F Drake, N.M. Cassar, and R.A. Nistor, Phys.Rev.A 65, 054051 (2002).
[6] Vladimir I. Korobov, arxiv 0204079v2 (2002)

2010/6/7 updated This site is link free.