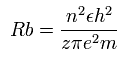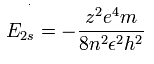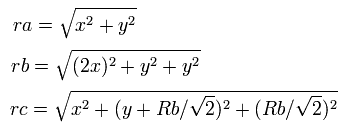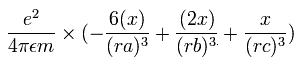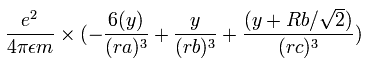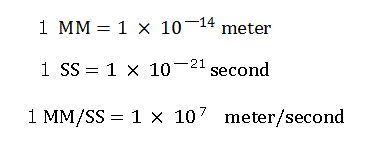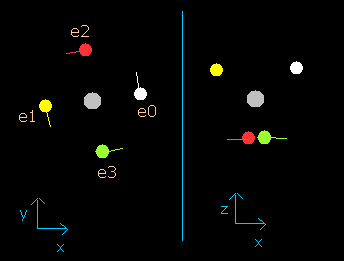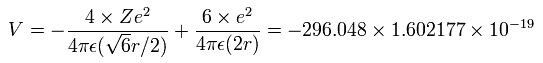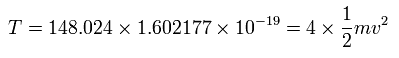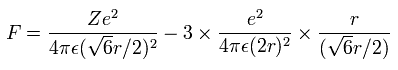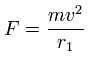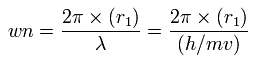新しいボーア模型による炭素(C)
トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは実在しない
我々の新しいボーア模型によって、ヘリウム原子の基底状態エネルギーの計算で、量子力学的な変分法よりも正確な結果をだすのに成功した。(トップページ参照のこと)。
この成功した新ボーア模型では、ヘリウム原子 (He) の2つの電子は、ちょうど1ド・ブロイ波長の互いに垂直な軌道上を運動している。
また、この新しい原子模型は、パウリの排他原理の現象も正確に説明できる。なぜなら、この新しいボーアの2電子原子には、3つめの電子が入りこむスペースがないからだ。
驚くべきことに、この新しいボーアのヘリウム構造は、他の2電子原子(イオン)である、リチウムイオン (Li+)、ベリリウムイオン (Be2+)、ホウ素イオン (B3+)、炭素イオン (C4+) にも正確にあてはめることができた。
(このページを参照のこと。)
さらに、3電子原子である、リチウム原子 (Li) のイオン化(基底状態の)エネルギーも、近似的なボーア模型の”2S”軌道を使用して、計算することができた。(このページも参照のこと。)
ボーア模型の炭素イオン (C 3+)
ここでは、、3電子原子である、炭素イオン (C3+) に挑戦することにする。
炭素イオン (C3+) は、1S軌道に2つの電子と、2S軌道に1つの電子をもっている。
1Sの2つの電子は、6e+ の原子核に強くひきつけられているため、2S の電子に比べてかなり原子核に距離的に近いところにある。
つまり、近似的に、我々は2S電子が、 +4e 原子核 (+6e - 2e = +4e) の周りの2ド・ブロイ波長の円軌道を回っているとみなすことができる。
(これは、我々が2S電子において、近似的に水素原子の式を使えることを意味する。)
ボーア模型によれば、n × ド・ブロイ波長の軌道の半径 (Rb) は、次のように なる。
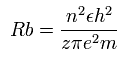
( z = 1 と n = 1 のとき、 Rb はいわゆる”ボーア半径”となる。)
C3+ の 2S 電子では、原子核の陽電荷 z は、4+ と近似的にみなすことができ(上を参照)、また、n は 2 である。
計算すると、この Rb は 1 × ボーア半径 ( = 0.5291 × 10-10 meter ( = 5291 MM ) となる。
(ここでは、便宜のため次のような新しい単位を使う。 1 MM = 10-14 meter, 1 SS = 10-22 second, 1 MM/SS = 108 m/s.)
水素様原子のエネルギー準位は、
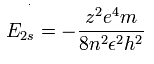
C3+ の 2S 電子では、n=2 と z=4 をこの式に代入する。
そのため、炭素イオン (C3+) の原子模型をつぎのように仮定できる。
Fig. 1. 炭素イオン (C3+) 模型
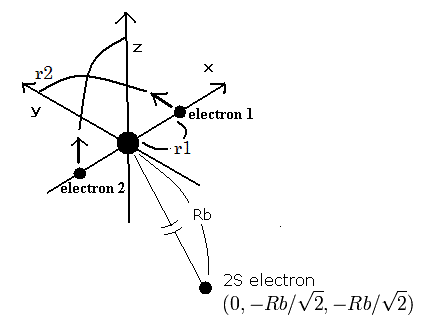
1Sの2つの電子はなるべく2S電子を避けるように運動する。そこで、我々は2S電子を Fig. 4. に示すように ( 0, - Rb / √2, - Rb / √2 ) に固定する。
(Fig.1 は3つの電子の相対的な位置関係を示している。実際は、この2Sの電子は1Sの電子よりもゆっくりと核の周りを周回している。)
C4+ のように (このページを参照のこと)、電子1が、(x, y, 0) にあるとき、電子2は、 (-x, 0, y) にある。
つまり、各粒子間の距離は、
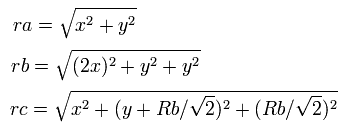
となる、ここで、ra は電子1と核の距離、rb は2つの 1S 電子間の距離、rc は電子1と 2S の電子の距離である。
電子1の加速度 (m/sec2) の x成分は、
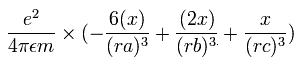
となる。
同様に、電子1の加速度 (m/sec2) の y成分は、
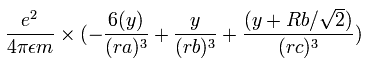
となる。
また、C4+ のときのように、1S 軌道の 1/4 周に含まれるド・ブロイ波の数を計算する。
サンプルJAVAプログラム (C3+)
Table 1 は、C3+ において、 last VY (電子1が 1/4 周した後の速度の y 成分)がゼロに一番近い時の結果を示す。
Table.1. last VY がゼロのときの r1 と WN の結果 (C3+)。.
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|
| -930.0 | 944.0 | 0.25211 | 1.00844 |
| -935.0 | 939.0 | 0.25138 | 1.00552 |
| -940.0 | 933.5 | 0.25067 | 1.00268 |
| -944.7 | 928.5 | 0.25000 | 1.00000 |
| -950.0 | 923.0 | 0.24924 | 0.99696 |
| -955.0 | 917.5 | 0.24854 | 0.99416 |
| -960.0 | 912.5 | 0.24785 | 0.99140 |
この結果は、C3+ イオンの基底状態エネルギーが -944.70 eV のとき、軌道の長さがド・ブロイ波長の ちょうど 1.00000 倍になることを示している。
炭素イオン (C3+) エネルギーの実験値は -64.49390 - 392.08700 - 489.99334 = -946.574 eV である。
つまり、計算誤差は、わずか 1.87 eV ( 0.20 % ) である。
(この小さな計算誤差は、おそらく、”近似的な”2S電子軌道を用いたことによると考えられる。)
このことは、炭素イオン (C3+) の3つの電子が、 Fig.1 に示すように運動していると言ってほぼ間違いないということを意味する。
ボーア模型の炭素 (C) の4つの価電子の視覚化
中性の炭素 (C) においては、4つの 外殻 軌道の電子はどう動いているのだろうか?
炭素は、6つの電子をもっており、そのうち、2つの 1S 軌道の電子は 原子核にとても近づいており (上の C3+ のセクションを参照のこと)、4つの 外殻軌道の電子は、正四面体様に配置されていると考えられる。
つまり、近似的に、4つの外殻電子が +4e の中心核 (+6e-2e = +4e) の周りを周回していると仮定することができる。
(ここでは、4つの価電子の全エネルギーを -148.024 eV = 1 から 4 のイオン化エネルギーの合計と仮定する。)
そこで我々は、炭素原子の4つの価電子が、Fig.2-1 に示すように正四面体状に配置されていると仮定できる。
Fig. 2-1. 推定される炭素原子 (正四面体). 原子核=(0,0,0)
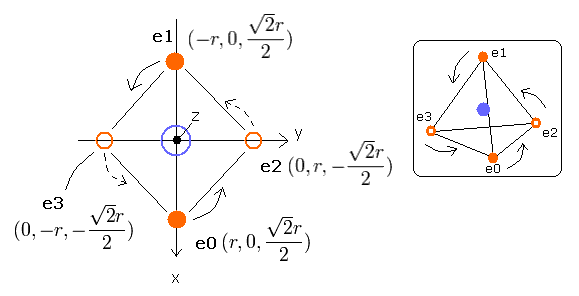
ここでは、次のサンプル JAVA プログラム (version 1.5 (5.0)) を使って画面上に炭素原子の電子の運動を視覚化してみることにする。
サンプル JAVA プログラム (炭素の視覚化)
このプログラムは少し長いので、中に示すソースプログラムをコピーして、テキストエディタ(メモ帳など)にそのまま貼り付けて、コンパイルすれば簡単に実行できる。
このプログラムの class file name は cavis1 なので、このデキストエディタを "cavis1.java" のファイル名で保存してコンパイルしてほしい。
このプログラムでは、炭素原子核は、灰色の円 (Fig. 2-2 参照)で表示している。
また4つの電子は、e0 (白)、e1 (黄), e2 (赤)、e3 (緑)の円でそれぞれ示してある。
x, y, z 軸は Fig.2-1 に示す軸と同じである。
左、真ん中、右の図はそれぞれ、x-y, x-z, y-z 平面を表している。
また、各電子の速度ベクトルは線で示してある。
Fig. 2-2. プログラム中の炭素原子核と4つの価電子 (wn=0)
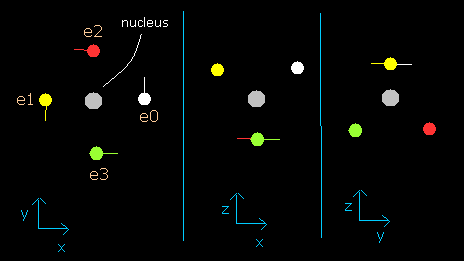
テキストボックス内の電子の各座標 (+X (MM), +Y (MM), +Z (MM)) は、この原子核からの”相対的な”位置座標を示している。
ここでは次のような新しい単位を用いている。
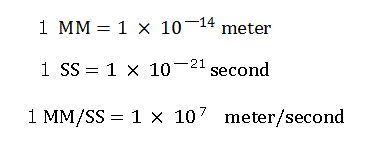
"nuc (MM)" は、核と各電子の間の距離を意味している。
"VX: VY: VZ" は電子の初速度の各成分の比を示している。
つまり、(VX: VY; VZ)=(100:100;0) は、(VX: VY: VZ) = (10:10:0) と同じ意味である。
スクロールバー (0.1 -- 2.0) の中から、ド・ブロイ波の数 (=wn) を選んで、"orbit" ボタンをクリックすると、このプログラムは、軌道に含まれるド・ブロイ波の数が wn になるまで電子軌道計算を続ける。
詳細な計算方法については、トップページを参照のこと。
微小時間 (1 SS) ごとに、4つの電子と核の間のクーロン力を計算し、その結果を基に各速度ベクトルを変化させていく。
また、各電子につき、微小区間に含まれるド・ブロイ波の数も計算していく。
(このプログラムでは、4つの価電子の全エネルギーは、第1〜4のイオン化エネルギーの合計である、-148.024 eV としている。)
このプログラムは、テキストボックスと模式図としての両方に、各電子の最後の座標と速度ベクトルの結果を表示する。
それから、"retur" ボタンをクリックすると、すべての電子は、また最初のスタートラインの状態に戻ることができる。
また、"radiu" ボタンの隣のテキストボックスに r (MM) (Fig.2-1参照) の値を入力して "radiu" ボタンをクリックすれば、Fig.2-1 に示すように、4つの電子の正四面体の大きさ(半径)が変化する。
最初に、r (MM) として、4890 の値を入力して "radiu" ボタンをクリックしてみる。
(この場合は、Fig.2-1 の r の値は 4890 (MM) となり、原子核と各電子の最初の距離 (=nuc) は 5989 MM となる。)
次に、スクロールバーの中から、ド・ブロイ波の数 (wn) として 0.5 を選んで、"orbit" ボタンをクリックしてみると、計算が開始して、次のようなイメージ結果が表示される。
Fig. 2-3. wn = 0.5 における炭素原子の電子
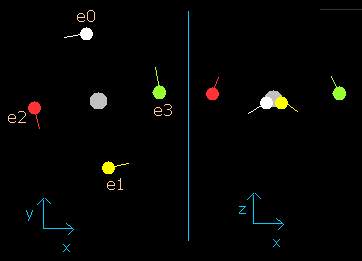
電子が、0.5 ド・ブロイ波長分の軌道を進んだとき (wn=0.5)、炭素の4つの価電子はすべて、x-y 平面近くに位置している (Fig. 2-3 右図)。
また、この地点 (wn=0.5) では、原子核と電子の距離は約 5976 MM である。
次に、"retur" ボタンをクリックして、wn=0 の最初の状態に戻ろう。
それから、スクロールバーの中で 0.9 の値をド・ブロイ波の数 (wn) として選び、また"orbit" ボタンをクリックする。(Fig.2-4)
Fig. 2-4. wn = 0.9 における炭素原子の電子
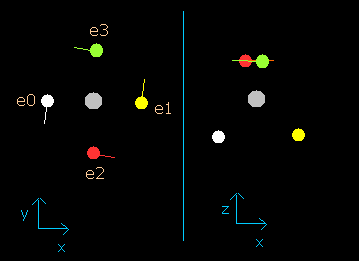
このイメージ結果は、電子が 0.9 ド・ブロイ波長分の軌道を進んだとき、炭素原子の4つすべての価電子は、その最初の位置から正反対のところに移動していることを示している。
wn=0.9 の地点では、原子核と電子の間の距離は最も短く ( = 5921 MM) なる。
また、"retur" ボタンを押して、今度は 1.9 の値を選択し、"orbit" ボタンをクリックしてみる。
結果は、Fig.2-5 に示すようになる。
Fig. 2-5. wn = 1.9 における炭素原子の電子 (=ほぼ wn=0.0 と同じ。)
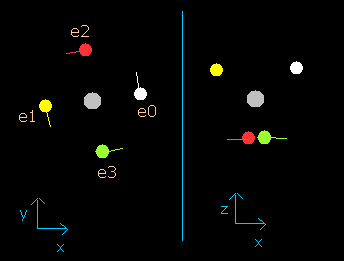
この結果は、4つすべての電子が、1.9 (ほぼ 2.0) ド・ブロイ波長分の軌道を進んだときに元の位置に戻ることを証明している。
(おそらく、これらの軌道は少しだけ歳差運動や揺れ運動をしていると思われる。)
上のプログラムでは、中心の仮の正電荷をちょうど +4.0e ( = +6e (原子核) -2e (2つの 1S 電子) = +4e) としている。
しかし、上のセクションで示したように、2つの 1S 電子は、約 930 MM ほど、+6e の炭素原子核から離れている。(それらは、核にくっついているわけではない。)
そのため、4つの外殻電子に影響を与える"実質的な中心電荷"は、おそらく +4.0e よりも少し大きくなるだろう。
そこで、ここでは、中心の仮の正電荷を +4.0e のかわりに +4.25e として、もう一度軌道計算をしてみることにする。
サンプル JAVA プログラム (中心の仮電荷 +4.25e )
このサンプルプログラムは、中心の仮の正電荷を除いて上に述べたプログラムと同じである。
このプログラムでは、電子の進んだ軌道の長さが ちょうど 2.0 ド・ブロイ波長分になったとき、炭素の4つの価電子すべてが 次に示すように、もとの位置に戻ることができる。
Fig. 2-6. wn = 0.0 と wn = 2.0 のときの酸素の価電子 (”実質的な”中心電荷 = +4.25e)
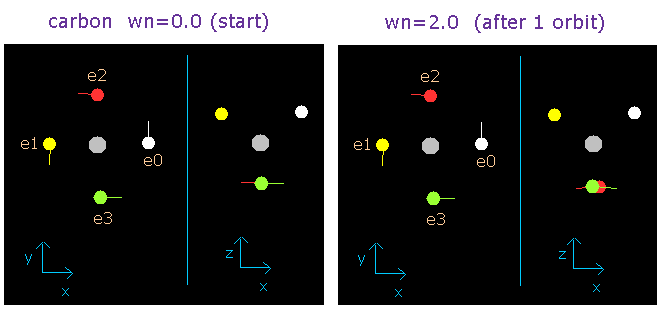
この結果はとても重要である。
4つの価電子の全エネルギーがある値 (=-148.024 eV) に決定すると、1軌道の平均の長さはだいたい一意的に決まる。
(このことは、全エネルギーの値を決めると、平均の軌道長、すなわち1軌道に含まれるド・ブロイ波の数が”自動的に”決まることを意味している。)
そして、この波の数が、中性の炭素原子の場合は 2.0 になることが証明された。
(つまり、この結果は、炭素原子の4つの価電子は、 2.0 ド・ブロイ波長の軌道上を運動していることを示している。)
上の C3+ の場合は 中心電荷を +4.0 としてほぼ正確な結果をだせた。これは、Fig.1 のスタート地点においては、この近似によって生じる誤差はわずかだからである。
このページ (ボーア模型における 1S 電子と 2S 電子の関係) も参照のこと。
中心の正電荷 (Z) がちょうど +4.0e (=+6e-2e) としたとき、1軌道に含まれるド・ブロイ波の数 (wn) は、 1.9 になる。
しかし、実際は2つの 1S 電子は +6e の原子核にくっついていないので、この中心電荷 (Z) を +4.25e (+4e より少し大きく) と仮定すると、上に示したように、1軌道のド・ブロイ波がちょうど 2.0 になった。
この 中心電荷が +4e よりも大きくなる (+4.25e) 効果は、とくに、第3や第4のイオン化エネルギーの値に含まれている。
なぜなら、価電子が減るにつれ、残りの価電子がより、+6e の核に近づいていくからである。
ここでは、このことを ビリアル定理 (Virial theorem) を用いて証明してみることにする。
我々は、次に示すように炭素の4つの価電子が +Ze の中心電荷の周囲に”四面体状に”配置されていると仮定する。
Fig. 3. 炭素原子の価電子 ("有効" 中心電荷 = +Ze)
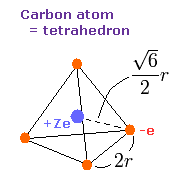
Fig. 3 では、正四面体の一辺の長さを 2r とする。
ビリアル定理によれば、”平均の”全位置エネルギー (V) と運動エネルギー (T) は次の関係にある。
< V > = -2 × < T > , E = V + T
4つの価電子の全エネルギー (E) は、-148.024 eV なので、この位置エネルギー (V) は、2 × -148.024 = -296.048 eV となる。
Fig. 3 の模型を使って、電子ー核、 電子ー電子の間の電位を計算していくと、全位置エネルギー V ( 単位 eV --> J ) は次のように示せる。
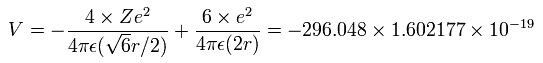
また、4つの電子の全運動エネルギー (T) は、148.024 (eV) である。
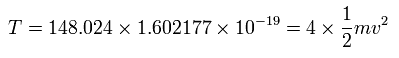
また、Fig.3 より、電子1つにはたらくクーロン力の合計 (F) は(核方向の力になるが)、次のようになる。
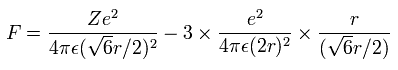
上の式の T 中の速度 (v) と、力 F の値を用いて、遠心力がこの力 (F) に等しいと仮定する。
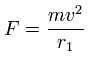
この r1 は、この関係式で初めて登場する 仮の半径である。
この r1 を用いて、次に示すように、1軌道に含まれる ド・ブロイ波の数 (wn) を計算することができる。
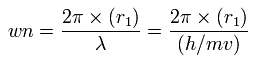
中心電荷 Z が +4.0 のとき、この wn は 1.87 (ほぼ 1.9) となる。
また、Z = +4.25 のとき、この wn は、ちょうど 2.02 になる。
つまり、我々はビリアル定理によって、このことを証明することができた。
C-C 結合 (例えば、エタン CH3-CH3などの ) は、同じ2つの炭素原子より成る。この点は、 H-C や H-O 結合と異なる。
つまり、もし、電子が炭素原子核のうちの片方に近づくと、その炭素原子核からのクーロン引力は、必ずもう片方の炭素原子核のクーロン引力よりも強くなる。
これは、すなわち、C-C 結合の電子は、炭素原子核のどちらか、一方に主に属していると言える。
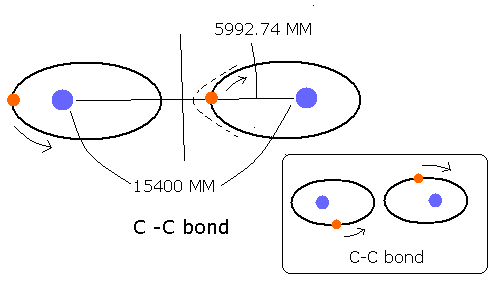
C-C 結合距離は、1.54 × 10-10 meter ( = 15400 MM ) である。
この結合距離の半分は、15400 / 2 = 7700 MM である。
上の一番長くなる距離 5993 MM は、良い結果と言える。なぜなら、それは、7700 MM に近いが、それを越えていないからである。(ただし、もう一つの炭素原子核のクーロン引力によって、少し伸びるが。)
(もし、上記の最も長い距離が 7700 MM を越えていると、電子は もう片方の炭素原子核のほうへ飛んで行ってしまい、これは、さきほどの説明と一致しない。つまり、最も長い距離(原子核と電子1の)は、7700 MM を越えてはならないのである。)
Fig. 4 推定される C-C 結合模型

2010/7/30 updated This site is link free.