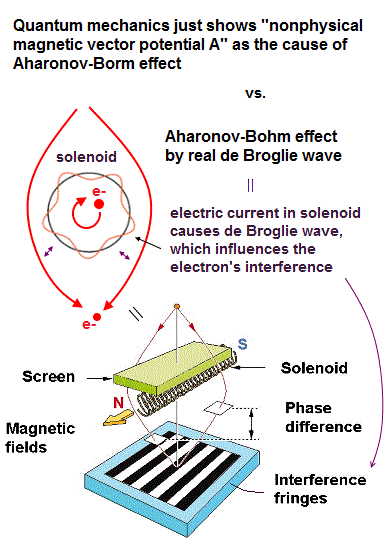
(Fig.1) Electrons flowing in the solenoid cause de Broglie wave around it.

It is known that even a single indivisible electron can interfere with itself in double-slit experiments.
The current unrealistic mainstream quantum mechanics claims that this single electron's interference in double-slit experiments is caused by an electron unscientifically splitting into many ( fictional ) parallel worlds.
An electron is known to generate de Broglie wave, which existence and interference were confirmed in many experiments such as Davisson-Germer and diffraction.
Using this real de Broglie wave traveling through real medium, we can naturally and realistically explain the double-slit interference of a single electron without relying on the fantasy quantum mechanical parallel worlds.
This electron's interference was affected by the long solenoid with electric current flowing inside it.
The long solenoid causes magnetic field only inside it, and generates almost no magnetic field outside the solenoid.
So the unphysical quantum mechanics started to claim that this change of electron's interference is due to the (unphysical) magnetic vector potential A allegedly generated around the solenoid's electric current, which is called "Aharonov-Bohm effect".
But quantum mechanics is unable to explain what this magnetic vector potential A really is, except for showing just the nonphysical meaningless mathematical symbols.
When an electron is moving and flowing as the electric current, it is known to generate de Broglie wave (= spreading over some area ), which can naturally affect the double-slit interference of the electron's de Broglie wave.
As a result, Aharonov-Bohm effect or electron's interference is caused by the realistic electron's de Broglie wave, Not by nonphysical magnetic vector potential or fictional quantum mechanical parallel worlds.
(Fig.2) Lorentz magnetic force = centrifugal force, and the circumference of an integer times de Broglie wavelength can explain the experimentally-verified magnetic flux quantum
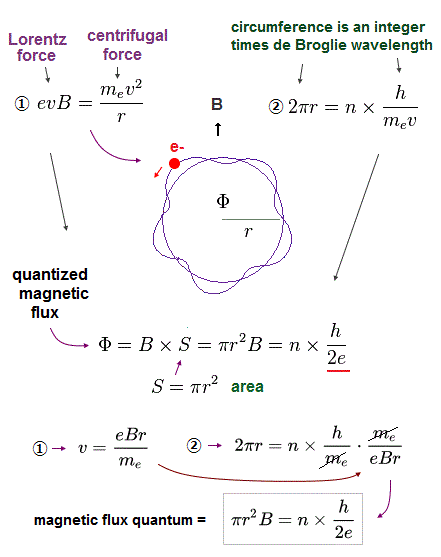
It is known that the magnetic flux threading a superconducting loop or hole is quantized as an integer (= n ) times magnetic flux quantum (= h/2e where "h" is Planck constant and "e" is the electron's charge ).
The unphysical quantum mechanics tries to explain this quantized magnetic flux using nonphysical phase θ and unrealistic Cooper pair (= two repulsive electrons paradoxically attract each other ? this-p.1 ) without showing any more concrete description.
We can naturally explain this magnetic flux quantum (= h/2e ) or Josephson constant (based on Josephson junction in SQUID = quantum tunneling ) using the realistic electron's de Broglie wave in Bohr-Sommerfeld model ( this-p.6(or p.1 )-last-paragraph ).
This-p.7(p.4)-3rd-last-paragraph says "Wee see that the magnetic flux through a superconducting loop is quantized similar in fashion to the Bohr-Sommerfeld quantization"
When the electron inside the superconductor is moving in a circular orbit under the applied magnetic field B, the magnetic Lorentz force = evB (= "v" is the electron's velocity, "B" is the applied magnetic field ) is equal to the centrifugal force (= mv2/r, where r is the radius of the electron's circular orbit ).
In order to avoid the destructive interference of the electron's de Broglie wave, the circumference (= 2πr ) of the electron's orbit should be an integral multiple of de Broglie wavelength (= λ = h/mv ).
From these two basic conditions, we can naturally derive the experimentally-verified magnetic flux quantum (= Φ = h/2e = πr2B ) in a realistic way without relying on the ad-hoc unphysical quantum mechanical phase or order parameter.
↑ It seems quantum mechanics desperately tries to avoid the word "de Broglie wave (= though, quantum mechanics heavily relies on de Broglie wave )", instead, quantum mechanics tries to use the more abstract (nonphysical) concept of "phase θ (= which actually means de Broglie wave's phase )"
Due to this quantized magnetic flux caused by an integral multiple of electron's de Broglie wave, the electric conductance (or resistance ) is changed with a periodicity of h/2e ( this p.4, this p.4 ).
See this.
(Fig.3) quantum Hall effect or Hall conductance (= 1/resistance ) in two dimensional electron system of low-temperature semiconductor under applied electric (= E ) and magnetic (= B ) fields.
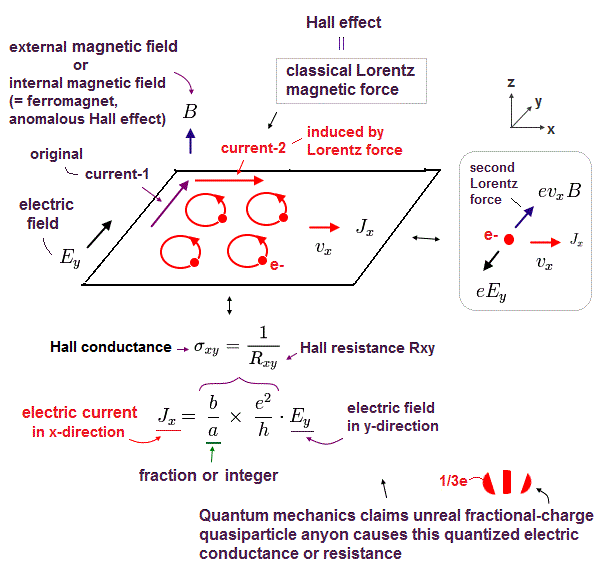
Hall effect or Hall current Jx is induced in the direction perpendicular to the original electric current-1 by applied external electric field Ey through classical magnetic Lorentz force under magnetic field B (= z direction ).
When this magnetic field B is due to internal magnetization (= caused not by unreal spin but by realistic orbital motion ) like in ferromagnet, this is called anomalous Hall effect (= AHE ).
This-p.1-introduction-2nd-paragraph says
"Whereas the ordinary Hall
effect of classical physics requires an external magnetic field, the anomalous Hall effect requires only
a magnetisation...ferromagnets "
The ratio of the induced electric current-2 (= x-direction ) to the original current-1 or electric field E (= y-direction ) voltage is called Hall conductivity (= σxy ) equal to 1/Rxy (= Rxy or ρxy is called Hall resistance or resistivity, this p.4-5, this p.11-12, this p.30 )
It is known that electrons can be moving around as electric current, confined in the thin layer (= 10~30 nm ) between some semiconductors and insulators called two-dimensional electron gas (= 2DEG ) system at very low temperature ( this p.2 ).
In this cold two-dimensional electron system, when the external magnetic field (= B ) is applied in z direction, and the external electric field (= E ) is applied in y directions, the electric Hall conductance (= σxy = reciprocal of resistance Rxy or ρxy ) expressed as the ratio of the electric current Jx in x direction to the electric field Ey in y direction becomes an integer or fraction of e2/h ( this p.2-4, this p.13, this p.4 ).
↑ This (integer or fractional) quantized electric (Hall) conductance or resistance is called ( integer or fractional) quantum Hall effect.
Real Bohr-Sommerfeld's de Broglie wave is known to explain this quantum Hall effect ( this-p.16, this-4~5th-paragraphs, this-p.15 ).
The current unphysical quantum mechanics can only explain this (fractional) quantum Hall effect or electric conductance using unreal fractional-charge quasiparticles called "anyon ( this p.14-16, this p.3-left, this-p.8-22 )."
We prove that these integer and fractional quantum Hall effect or electric conductance can be perfectly explained by the realistic electron's de Broglie wave instead of unrealistic quantum mechanical quasiparticles.
Quantum Hall effect is said to be used for determining some fundamental physical numbers such as Planck constant (= metrology. this-middle-quantum hall effect application ).
But we can determine those constants also by other methods, so quantum Hall effect is useless due to its needing very low temperature.
So quantum mechanics tries to associate the useless quantum Hall effect with hopeless topological quantum computers based on unreal fractional-charge quasiparticles ( this-middle~ ).
(Fig.4) electric force (= eE ) is equal to magnetic force (= evB )
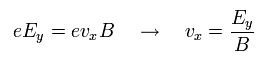
We derive the fractional and integer quantum Hall effect or Hall conductance (or resistance ) from the realistic electron's de Broglie wave.
When the whole electron is moving in x direction with the speed of vx under the external electric (= Ey in y direction ) and magnetic (= B in z direction ) fields, the electric force (= eEy ) becomes equal ( balanced ) to the magnetic force (= evxB ) like the upper equation.
(Fig.5) each circular current's area (= πr2 where r is radius ) in quantized Hall current
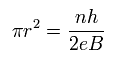
Under the external magnetic field B (in z direction ), the electron's orbit in semiconductor is quantized due to their de Broglie wave interference.
See Fig.2 from which we can obtain the above Fig.5
(Fig.6) Electric current Jx under the external electric (= Ey ) and magnetic (= B ) field.
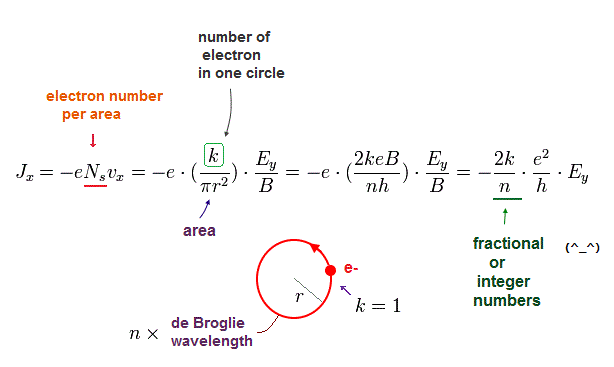
The electric current J is expressed as the charge density (= e × electron's number density per area ) multiplied by the electron's velocity vx.
When the electron's orbit is quantized by de Broglie wave interference, the number of electrons (= k ) contained inside the circular orbit's area (= πr2 ) or electron's density is expressed as k/πr2.
From Fig.4 and Fig.5, we can get the equation of the upper Fig.6 where the Hall conductance becomes 2k/n × e2/h ( this p.6~8 = Hall resistance R is reciprocal of conductance = R = n/2k × h/e2 ), where k is an integer or electron's number contained in one orbit with n × de Broglie wavelength.
This value of 2k/n can be an arbitrary integer or fraction when we choose different combinations of integers k and n, which can explain the real fractional and integer quantum Hall effect, based on real de Broglie wave's quantization.
As shown in Fig.8 and Fig.9 where each orbit closely surrounded by six other orbits in hexagonal way, the same phase (= an electron + the other orbit's hole ) of de Broglie waves tends to attract and tries to contact each other as much as possible, and the flexible electron's de Broglie wave orbits can reduce the gap.
(Fig.6') Fractional or integer quantum Hall resistance (= 1/conductance )
The upper Fig.6' shows when magnetic field is stronger, Hall resistance R increases.
↑ As the applied magnetic field B is stronger, each circular current area becomes smaller (= densities of positive nuclei remain the same ), which increases Coulomb repulsion between conducting electrons, as shown in Fig.3 and Fig.6.
↑ Due to this stronger Coulomb repulsion between electrons and the upper limit of the number of valence (= or conducting ) electrons, as the applied magnetic field B is stronger (= each circular current area becomes smaller ), the number of circular current's empty holes of electrons increases, so Hall resistance R (= or ρ ) increases (= Hall current or conductance decreases ) as the applied magnetic field B increases.
(Fig.7) Electron's de Broglie wave
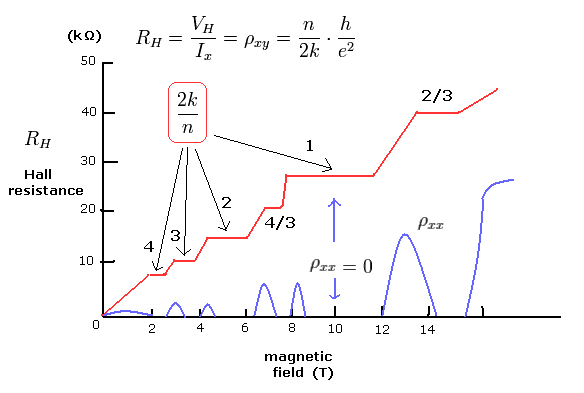
In order to avoid the destructive interference of electron's de Broglie wave, each electron's orbit must be an integer times de Broglie wavelength.
One de Broglie wavelength consists of a pair of the opposite phases.
(Fig.8) When each 2×de Broglie wavelength orbit ( n = 2 ) contains one electron (= k = 1 ), it becomes an integer quantum Hall effect.
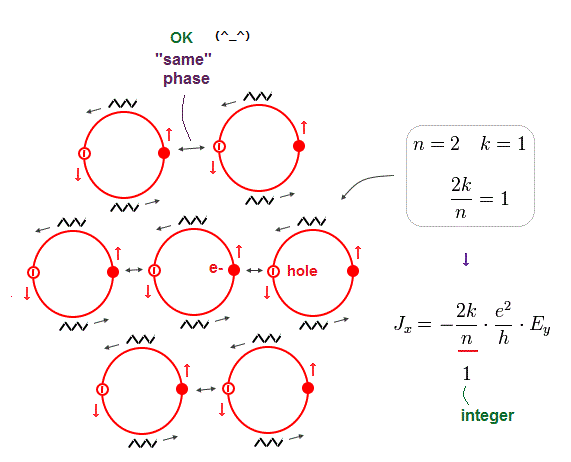
As shown in the upper figure, when each orbit with 2 × de Broglie wavelength (= n = 2 ) contains one electron (= k = 1 ), it can explain an integer quantum Hall effect where the Hall conductance is 1 (= 2k/n = 1 ) × e2/h
(Fig.9) Each electron can pass an empty hole of the neighboring atom
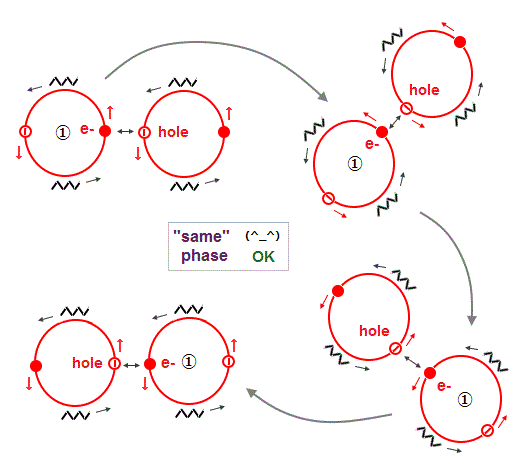
In the case of the integer quantum Hall effect of Fig.8, each electron can pass an empty hole of the neighboring orbit safely and smoothly as electric current.
(Fig.10) Integer quantum Hall effect with integer quantized electric conductance (or resistance ).
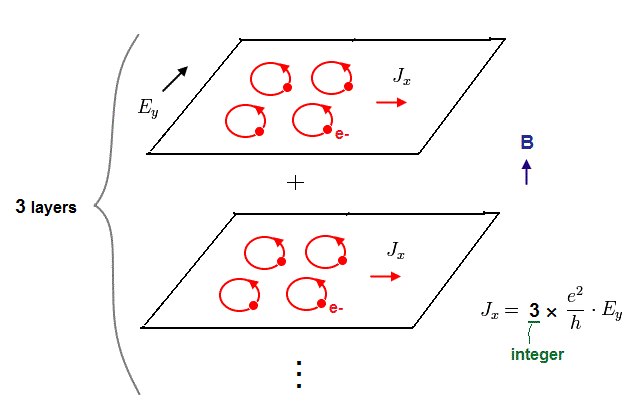
Basically, the two-dimensional electron gas system (= 2DEG ) has some thickness of about 10~30 nm, which can contain multiple layers of electric current (= because one atomic diameter is about 0.1 nm ).
When three layers of electric currents are flowing, this becomes the integer = 3 quantum Hall effect or 3 × Hall conductance of 1.
In this way, we can explain an arbitrary integral number of quantum Hall effect using the realistic electron's de Broglie wave.
(Fig.11) Real mechanism causing fractional quantum Hall effect without using unreal quantum mechanical fractional-charge quasiparticles.
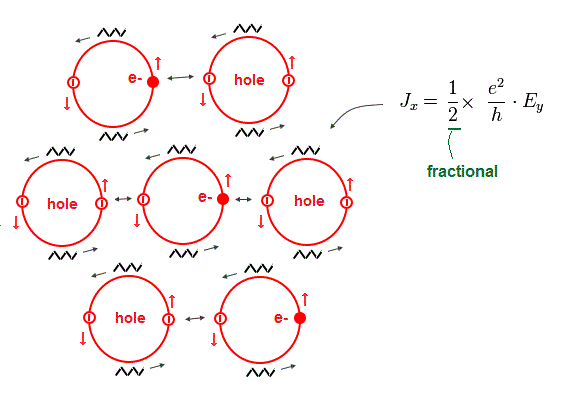
As shown in the upper figure, when every two orbits contain only one electron (= k = 1/2, n = 2 ), it becomes the fractional quantum Hall effect with fractional Hall conductance of 1/2 (= 2k/n = 1/2 when k = 1/2 and n = 2 ) × e2/h.
When every three orbits contain only one electron, it becomes 1/3 fractional quantum Hall effect.
When there are five layers of the electric current of this 1/3 quantum Hall effect, it becomes 5/3 fractional quantum Hall effect.
In this way, we can successfully explain an arbitrary number of fractional quantum Hall effect using the realistic electron's de Broglie wave without unreal quantum mechanical fractional-charge quasiparticles ( this-p.10-12 ).
The electric conductance (= reciprocal of electric resistance ρxy ) and how many layers of electric current are involved are affected by the strength of applied magnetic field B. = More stronger magnetic field B is applied, the orbital radius r is smaller = number of electrons (= k ) contained in one orbit is smaller ( due to stronger repulsion between neighboring electrons ) = the electric conductance is smaller (= electric resistance is bigger), and the number of electric current layers becomes smaller.

Feel free to link to this site.