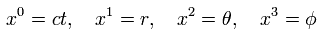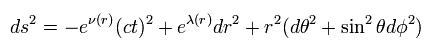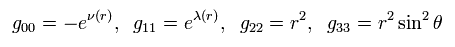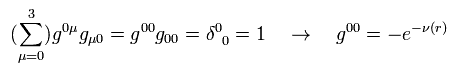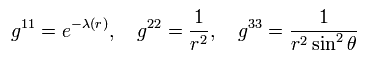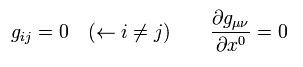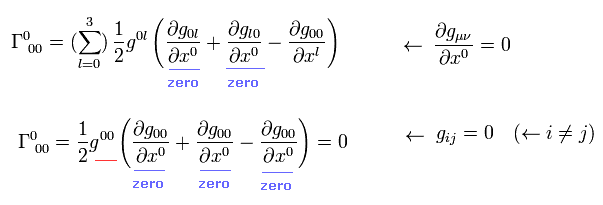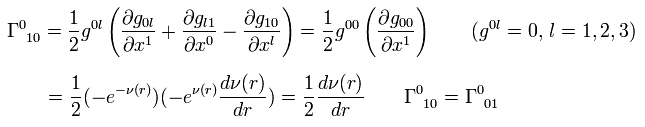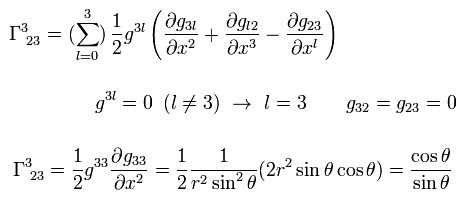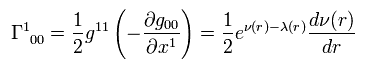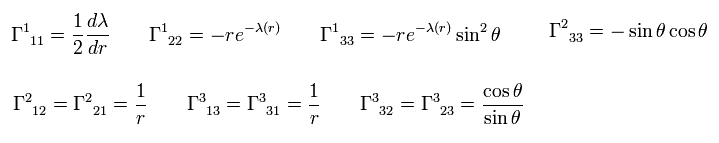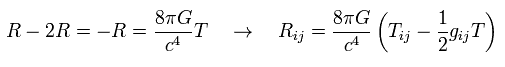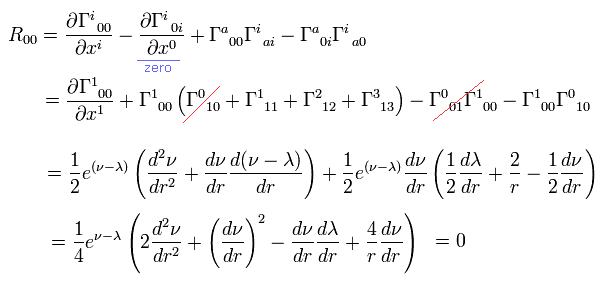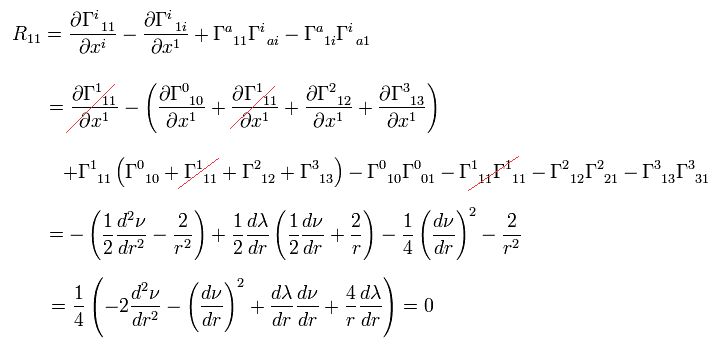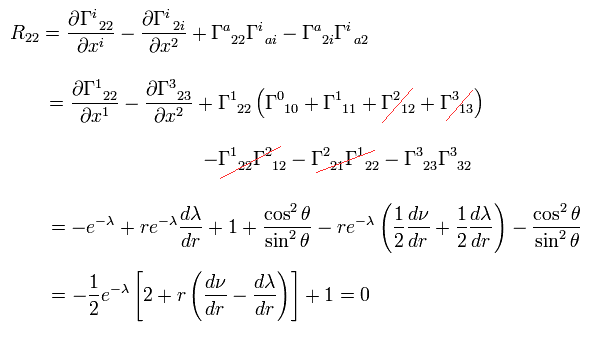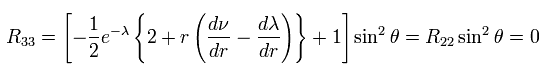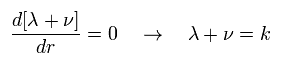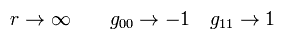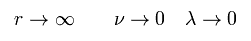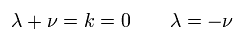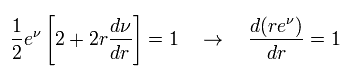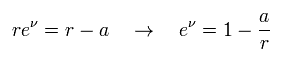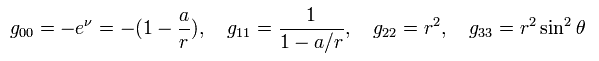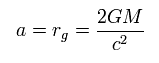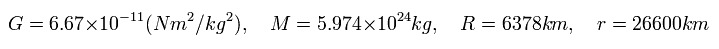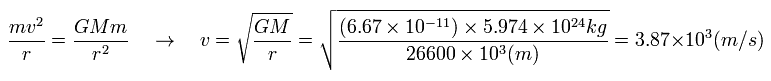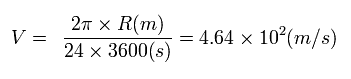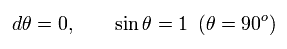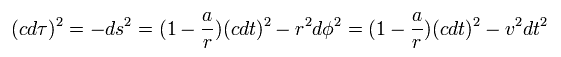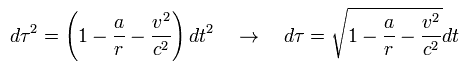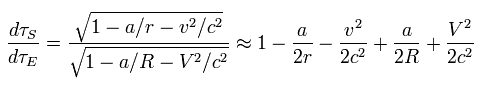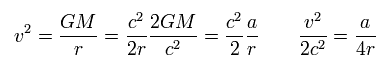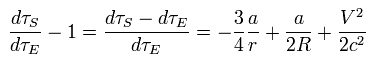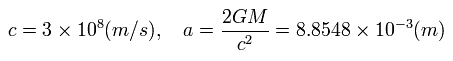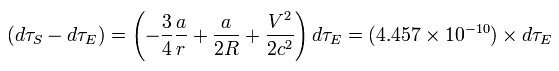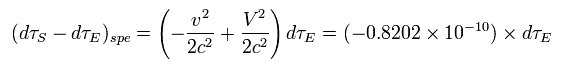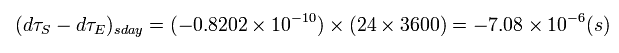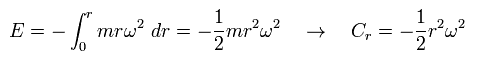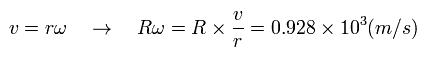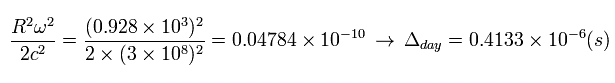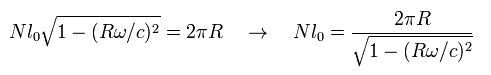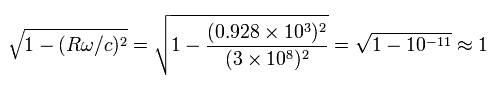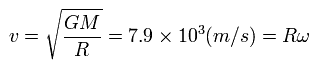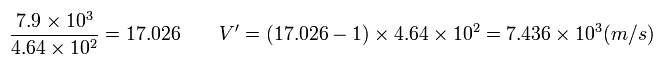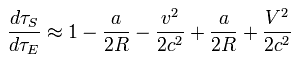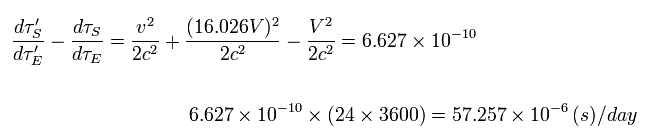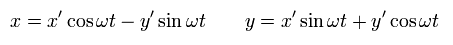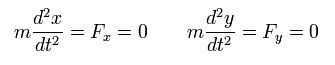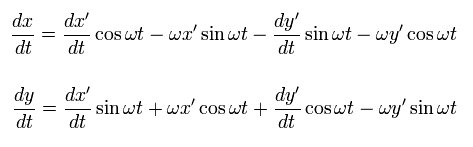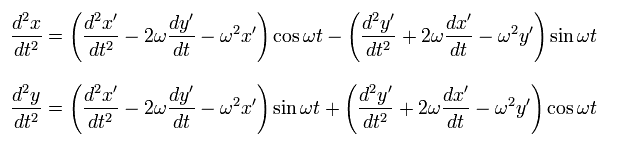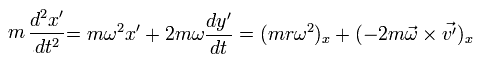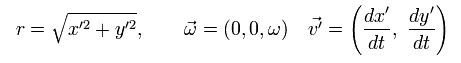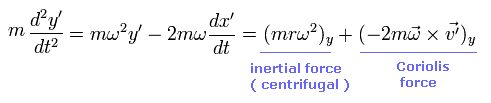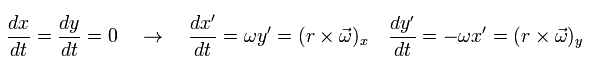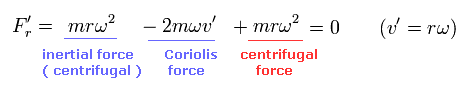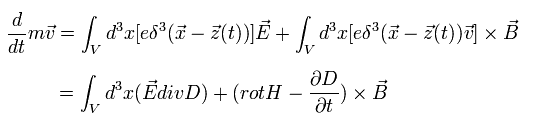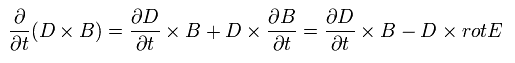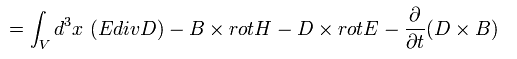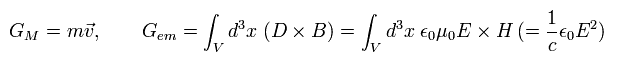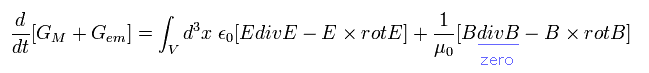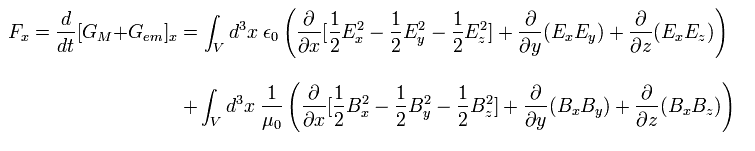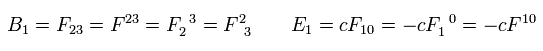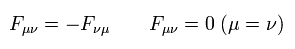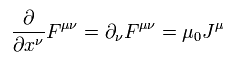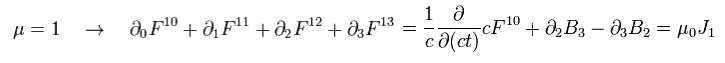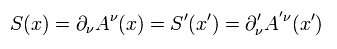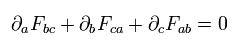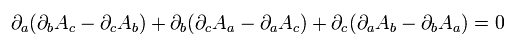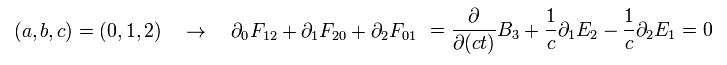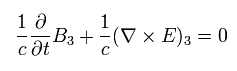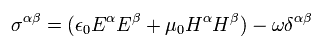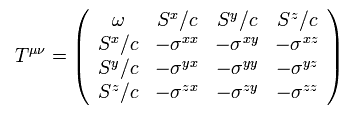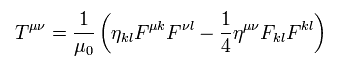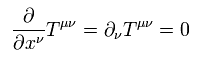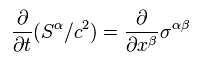GPS satellite clock really shows relativity ?
Home page
Einstein is wrong (1/30/2025)
GPS does Not use relativity
Derivation of Schwarzschild solution.
If you have not read this page ( to Eq.119 ), read it first.
Schwarzschild solution (metric) was the first solution of Einstein equation in 1915 and predicts the existence of black hole.
In this case, point particle of mass M is at the origin, and the gravitational field is spherically symmetric and static (= time derivative is zero ).
( So, Schwarzschild metric thought about the things like the earth from the beginning. )
Using the polar coordinate of
(Eq.1)
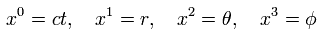
The metric tensor gμν × each coordinate can be expressed as ( considering spherical symmetry ),
(Eq.2)
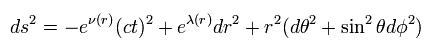
where
(Eq.3)
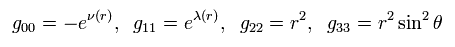
Other metric tensors are supposed to be zero.
And we define gμν, as follows,
(Eq.4)

Generally, unlike Minkowski metric tensor, gμν is not equal to gμν
From Eq.3 and Eq.4, we have
(Eq.5)
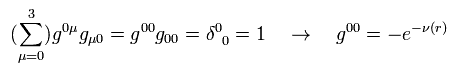
and
(Eq.6)
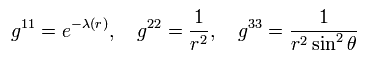
Calculation of each Christoffel symbol.
As shown on this page, Christoffel symbol is
(Eq.7)

The metric g is static and limited to Eq.3,
(Eq.7-2)
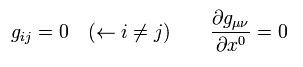
From Eq.3, Eq.5, Eq.6, and Eq.7, we obtain
(Eq.8)
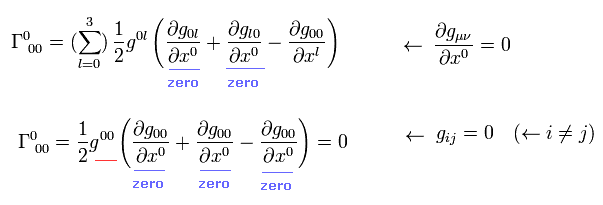
so, Eq.8 Christoffel symbol is zero.
Like Eq.8, almost all Christoffel symbols are zero due to very strict restrictions of Eq.7-2.
In the same way,
(Eq.8-2)
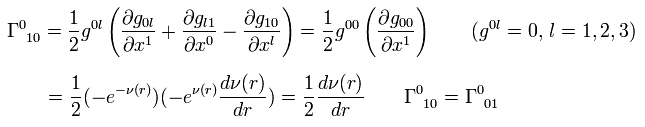
(Eq.8-3)
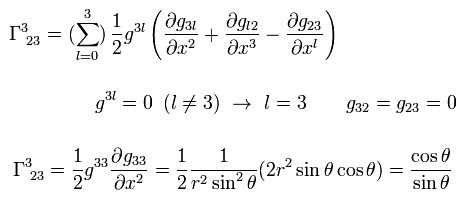
and
(Eq.9)
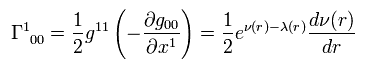
In the same way,
(Eq.10)
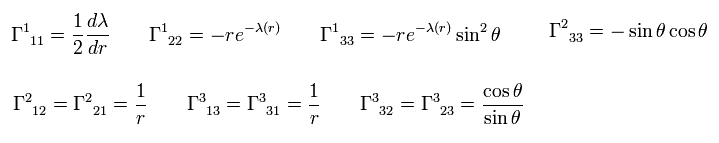
All other Christoffel symbols are zero.
Ricci tensor is
(Eq.11) .

(If you contract the first and fourth indices of the Riemann curvature tensor, put minus sign to Eq.11. )
As shown in Eq.112 of this page, Ricci tensor can be expressed using the energy momentum tensor T,
(Eq.112')
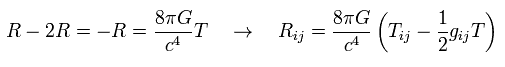
In the vacuum, all energy-momentum tensors are zero, so Ricci tensors are zero, too.
( Caution: Riemann curvature tensors are not zero. )
Calculation of Ricci tensor.
From Eq.8,9,10 and Eq.11, we get
(Eq.12)
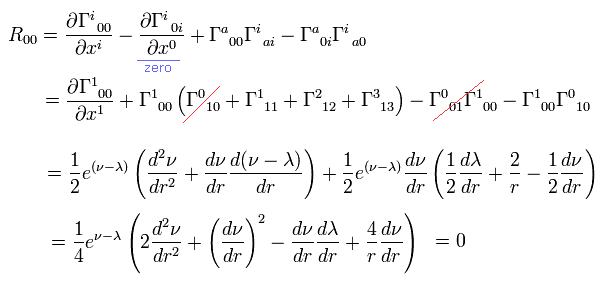
(Eq.13)
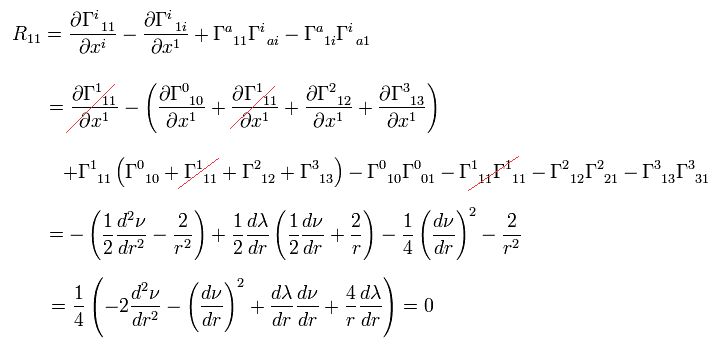
(Eq.14)
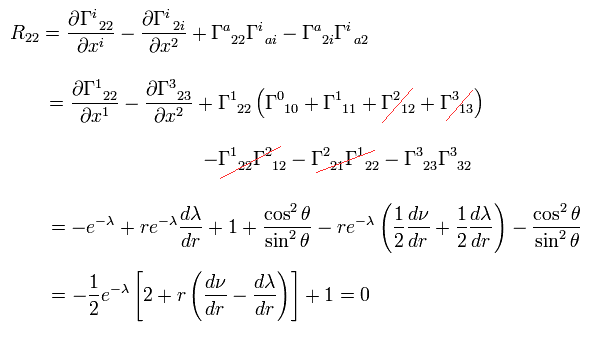
(Eq.15)
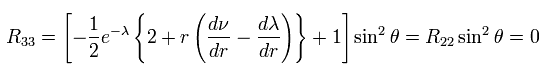
Substituting Eq.13 into Eq.12, we get
(Eq.16)
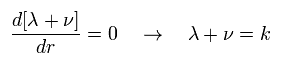
where k is a constant.
At the place of r → ∞, the gravity is supposed to be zero (= g becomes Minkowski metric tensor),
(Eq.17)
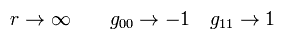
From Eq.3 and Eq.17,
(Eq.18)
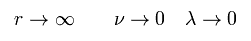
From Eq.16 and Eq.18, we get
(Eq.19)
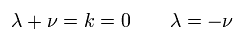
Substituting Eq.19 into Eq.14, we obtain
(Eq.20)
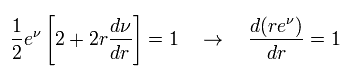
Integrating Eq.20
(Eq.21)
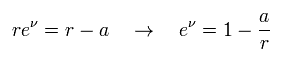
where a is a constant.
Calculation of metric tensor "g".
From Eq.21, Eq.19, and Eq.3, each metric tensor is
(Eq.22)
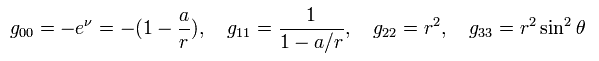
As shown in Eq.124 (or Eq.107 ) of this page, we have to match
the Newtonian gravitational potential φ(r) = -GM/r.
So g00 needs to be
(Eq.124')

From Eq.22 and Eq.124', "a" means "Schwarzshild radius" of
(Eq.23)
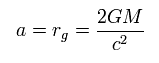
As a result, Eq.2 becomes (= Schwarzshild solution )
(Eq.24)

GPS satellite time correction does NOT use relativity.
Here we use next values
(Eq.25)
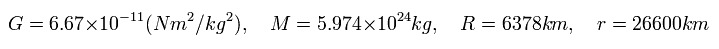
where G is "gravitational constant", and M is the mass of the earth.
R is the radius of the earth, and r is the distance between the artificial satellite and the center of the earth.
Suppose the centrifugal force of the satellite is equal to the gravity,
(Eq.26)
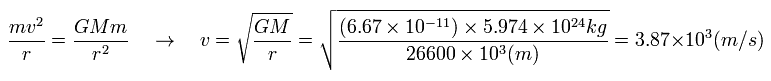
v of Eq.26 is the velocity of the satellite (with respect to the static earth).
And considering the earth rotates one time per day, the velocity V on the ground of the earth is
(Eq.27)
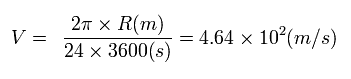
where the denominator means seconds per day.
From Eq.23 and Eq.24,
(Eq.28)

Here we suppose the distance r between satellite and the earth is constant ( dr = 0 ), and it is rotating like
(Eq.29)
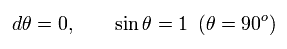
As shown in Eq.89 of this page, using Lorentz scalar proper time (= τ ) and the condition of Eq.29,
(Eq.30)
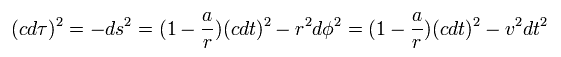
From Eq.30, the change of the proper time is
(Eq.31)
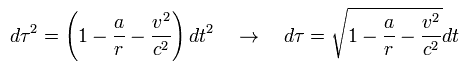
Using Eq.31, the ratio of satellite time (= τS ) to the earth time (= τE ) is
(Eq.32)
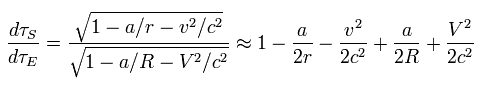
From Eq.26 and Eq.23,
(Eq.33)
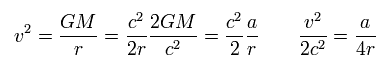
Substituting Eq.33 into Eq.32,
(Eq.34)
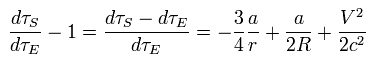
where
(Eq.35)
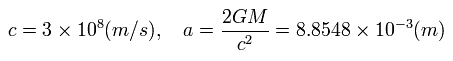
This means the Schwarzshild radius of the earth is only 0.9 cm.
From Eq.25, Eq.27, Eq.34, and Eq.35, we get the relation of
(Eq.36)
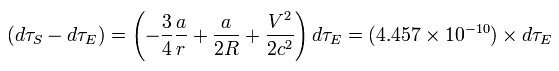
So the clock on the satellite ticks faster per day than the identical clock on the ground by
(Eq.37)

This means the relativistic correction (= special and general ) is about 38 microsecond per day.
If we pick only the special relativistic effect from Eq.32,
(Eq.38)
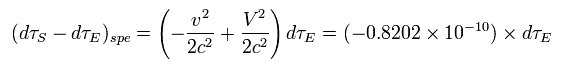
So if we consider only the special relativity, the satellite clock ticks slower per day by
(Eq.39)
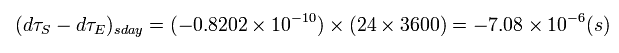
This means if we consider only general relativity, the satellite clock becomes faster by 38+7 = 45 microseconds per day.
Twin paradox in a satellite.
Twin paradox is a thought experiment in special relativity, in which a twin (= B ) makes a journey into space in a high-speed rocket and returns home to find he has aged less than his identical twin (= A ) who stayed in the starting point.
This result appears puzzling because each twin sees the other twin as traveling, and so, according to the time dilation (= proper time τ ), each should paradoxically find the other to have aged more slowly.
(Fig.1) Twin paradox.
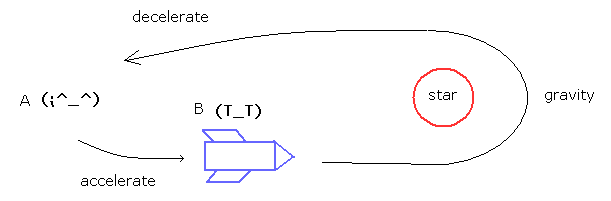
In this case, the ordinary textbooks say the B accelerates into the space, turns back by the star gravity, decelerates, and returns to the starting point.
So as a result, the proper time of B is always slower (due to acceleration and gravity), which is not "paradox".
But how about the GPS satellite in the above section ??
From the viewpoint of the satellite, the point on the earth is moving faster than the satellite.
( This means the special relativistic correction becomes opposite. )
So from the satellite, the clock of the satellite ticks faster per day by 45 + 7 = 52 microsecond !
So we need to correct the satellite clock 52 microsecond per day instead of 38 microsecond.
This is paradox.
Of course, different from the ordinary twin paradox, we have alreay considered the gravity influences upon them.
And the distance r is fixed and the satellite moves in the tangential direction, so r and R are not Lorentz-contracted.
So the signal light arrival time t is the same. ( t = (r-R)/c. )
The satellite is moving constantly at the velocity v ( it doesn't stop ).
It is said that the satellite time correction constantly needs special relativistic correction (= 7 microsecond per day ) to get the correct resutls.
So the constant time correction including general and special relativistic effects is unreasonable, I think.
As shown on this page (= violation of total charge conservation ), and this page (= right lever paradox ), the relativity includes other fatal paradoxes.
The important point is that these correction are very small ( only 38 microsecond per day ).
So it easily receives various other influences such as dielectric substance around the earth, and the signal light speed change in the atomosphere.
And the above calculations such as Schwarzschild solution are only "approximation".
This means that we can not affirm that the relativity is correct only from the above GPS time correction.
If there is "real ether" around the earth, the ether (and other dielectric substance ) becomes more condensed near the earth.
( GPS uses a atomic clock, in which the emitted electromagnetic wave frequencies are important. )
For example, the sound speed in the helium is much faster than in the air, because helium is lighter than the air.
As a molecule in the air is heavier, more time is needed to oscillate the molecule.
Twin paradox including centrifugal force.
(Fig.2) Satellite (= B ) rotating around the earth.
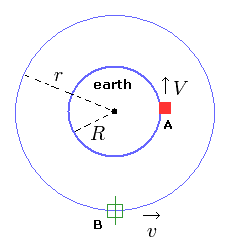
According to the general relativity, from the rotating coordinate system, the centrifugal force needs to be treated like gravity.
In this case, we introduce "centrifugal force potential" (= Cr ) like gravitational potential (φ = -GM/r ), as follows,
(Eq.40)
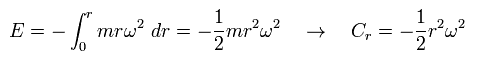
where r is radius, and ω means angular frequency.
( Of course, it is doubtful whether centrifugal force potential really causes "time dilation")
In the above condition, the satellite rotates around the earth two times per day, while the thing (= A of Fig.2 ) on the earth rotates one time per day.
So from the viewpoint of the satellite (= B of Fig.2 ), the thing on the earth rotates one time (= 2-1=1 ) in the opposite direction.
In this rotating coordinate system (= static with respect to the satellite ), the rotating velocity of the thing on the earth is equal to the original V of Eq.27. (Though its direction is opposite.)
Using the angular frequency ω of the satellite,
(Eq.41)
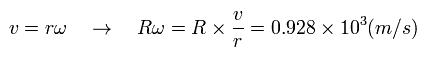
Using Eq.41, Eq.32 from the viewpoint of the rotating satellite (= B ) changes into
(Eq.42)
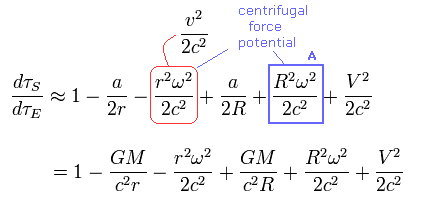
Comparing Eq.42 with Eq.32 (in the upper section ) of
(Eq.32)
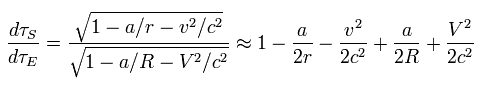
From the viewpoint of the rotating satellite, the satellite clock becomes faster than the rest frame.
The difference between them is A term of Eq.42.
Basically, the proper time must NOT change depending on the observer.
So this is completely a paradox.
Using Eq.41, this time difference is
(Eq.43)
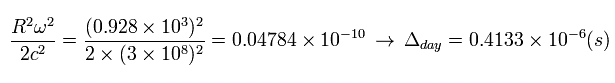
So the paradoxical time is about 0.4 microseconds per day.
This value is small. But day by day, this time paradox beomes bigger.
---------------------------------------------------------------
The length of one round orbit becomes a little longer in the rotating coordinate system.
Suppose from the satellite, the circumference of the earth is N × l0.
Here l0 means the length of one short stick. N is the number of these sticks put around the earth.
From the rest frame observer, each stick is Lorentz contracted. And the radius R of the earth is not contracted.
So, from the rotating satellite, the circumference (= N l0 ) of the earth looks
(Eq.44)
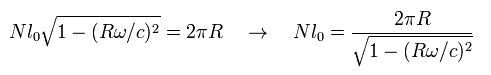
This means from the rotating satellite, the circumference of the earth becomes a little longer than 2π R.
( See also this page. )
But this effect is negligible, because
(Eq.45)
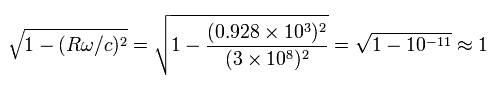
Of course, if we consider this effect of Eq.45, the paradoxical time difference of Eq.42 becomes bigger.
( V of Eq.42 becomes a little bigger. )
----------------------------------------------------------------
[ Satellite is rotating near the earth. ]
This paradox becomes remarkable, if the satellite is rotating just near the ground of the earth ( r = R ).
From Eq.26 (= centrifugal force is equal to gravity ), the satellite velocity v in this case becomes
(Eq.46)
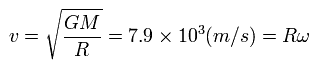
In this velocity of Eq.46, this satellite rotates around the earth about 17 times per day.
So from the viewpoint of the satellite, the velocity V' of the thing on the earth which rotates about 16 (= 17-1 ) times per day, is
(Eq.47)
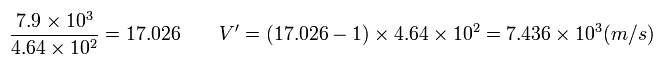
Like Eq.32, in the rest frame, the usual time differerce between the earth and satellite is
(Eq.48)
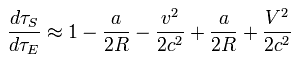
where r = R, and v and V (= Eq.27 ) means each velocity of satellite and the thing on the earth.
Using Eq.27, Eq.46 and Eq.47, from the satellite viewpoint, Eq.48 changes into
(Eq.49)
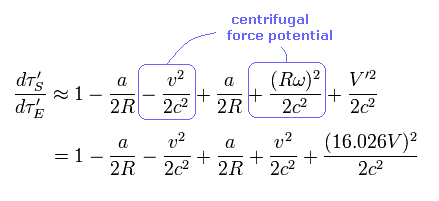
From Eq.48 and Eq.49, the paradoxical time difference ( per day ) becomes
(Eq.50)
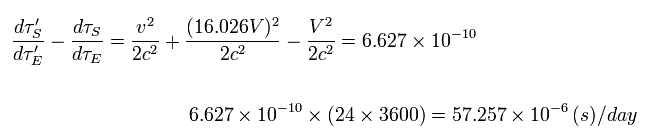
So in the case of the satellite rotating near the earth, this paradox is as big as 57 microseconds per day !
This means we can NOT use the special relativistic time correction in GPS satellite correctly.
As a result, GPS time correction does NOT mean the relativistic effects.
(Fig.3) Two identical satellites are moving in the opposite at the same velocity.
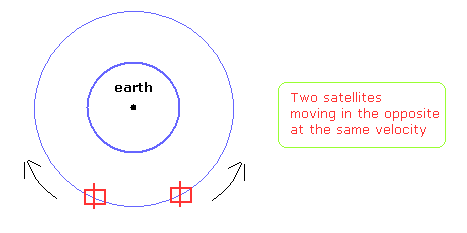
In Fig.3, two identical satellites are moving in the opposite directions at the same velocity on the same orbit.
Even if we consider all gravitational and centrifugal force potentials, this case clearly includes paradox and self-contradiction.
From one satellite's viewpoint, another satellite clock moves slower.
This corresponds to the opposite case, too.
( When passing each other, they can tell each other about their own clock times.)
So if we need the special relativistic correction in GPS system, this means relativistic effects are wrong.
What is "force" in general relativity ?
(Fig.4) What is the difference between "inertial" and "resistance" forces ?
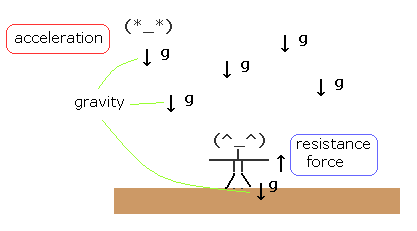
Here we explain why we treat gravity and inertial forces specially.
In Fig.4, one person is standing on the ground, who receives "gravity" and "resistance" force from the ground.
These forces are just equal and opposite, so he is at rest with respect to the (ground) earth.
Another person is falling by the gravity (= free fall ) .
In this case, according to general relativity, free falling person obeys only special relativity (= Minkowski spacetime), and the one on the ground obeys the usual general relativity.
What is the difference between them ?
(Fig.5) "global" force (= acceleration ) vs. "local" force.
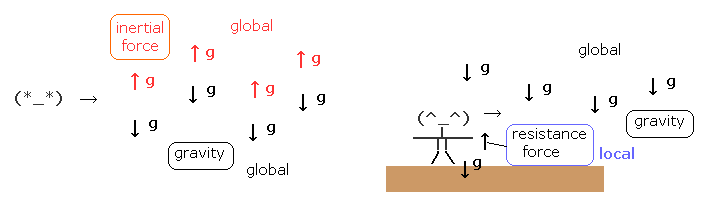
From the viewpoint of the free falling person (= left of Fig.5 ), all things in the world are accelerating upward.
This means "global change (= acceleration )".
Of course, the gravity also acts on all things in the world. So the gravity is "global" force (= acceleration ), too.
In the left case of Fig.5, these global forces (= accelerations ) of inertial and gravitational forces cancel each other, which means Minkowski spacetime (= no "global" forces ).
On the other hand, from the viewpoint of the person standing on the ground (= right of Fig.5 ), there is only one global force (= gravity ).
"Resistance" from the ground acts only on the standing person, which means "local" force.
In this case, he sees "Riemann" spacetime. As a result, only "global" forces influence strange "time dilation" and space distortion in the world.
[ Centrifugal force (potential) is "global" force in the rotating system. ]
(Fig.6) S' frame is rotating counterclockwise with respect to S.
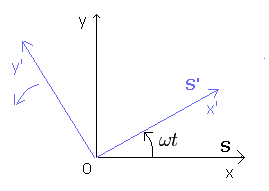
In Fig.6, S' frame is rotating counterclockwise with respect to S at the angular velocity ωt.
Each coordinate ( x', y' ) from S' and ( x, y ) from S satisfies
(Eq.51)
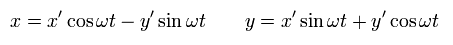
Suppose there is one thing at rest with respect to S, which receives no forces.
(Eq.52)
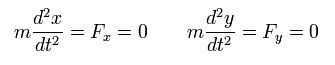
Differentiating Eq.51 with respect to the time t,
(Eq.53)
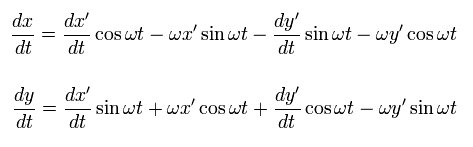
Differentiating Eq.53 one more time,
(Eq.54)
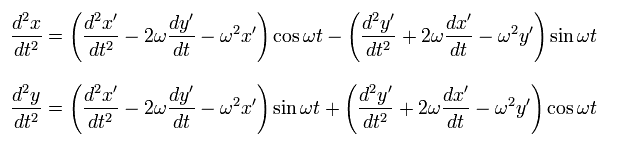
Multiplying the upper equation of Eq.54 by cos ωt and the lower one by sin ωt, and summing them,
we obtain ( under the condition of Eq.52 ),
(Eq.55)
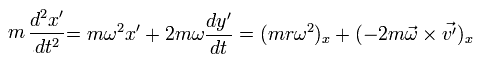
where
(Eq.56)
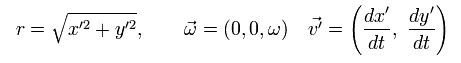
In the same way, multiplying the upper equation of Eq.54 by -sin ωt and the lower one by cos ωt, and summing them ( under the condition of Eq.52 ),
(Eq.57)
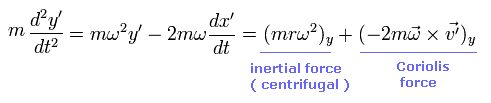
In Eq.55 and Eq.57, the first term means the inertial force, which originates from the centrifugal force.
And the second term means "Coriolis force".
The important point is that the inertial (centrifugal) force is a function of only position variables.
So all things existing in this world receives this inertial force, which means "global" force.
And with respect to these position variables, this inertial (centrifugal) force causes energy potential (= centrifugal force potential ), which is explained in the upper section.
On the other hand, Coriolis force is related only to the velocity, and is perpendicular to the velocity.
This means Coriolis force is NOT related to the potential energy, like Lorentz magnetic force.
From S' rotating frame, a thing at rest with respect to S is moving as,
(Eq.58)
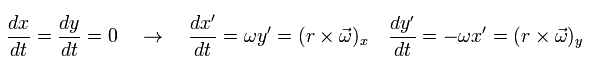
So this is rotating clockwise at the velocity rω from S'.
Of course, this thing is at rest in S frame, the radial force from S' must be zero, too.
Considering Eq.55, Eq.57, and Eq.58, the radial force from S' frame becomes
(Eq.59)
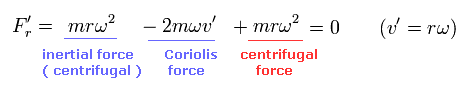
The first term of Eq.59 means global "inertial" force, which is caused by the rotation of the whole system.
As I said above, this force is related to the centrifugal potential.
And the second term is Coriolis force.
This is moving at the velocity rω, so it is influenced by Coriolis force perpendicularly.
And the last term is a ordinary "centrifugal force" from S' frame. ( See Eq.58 )
As a result, the radial force becomes zero from the viewpoints of both S and S'.
Relativistic form of electromagnetism.
This section is moved from Eq.51 - Eq.70 from this page.
[ Electromagneic momentum conservation ]
When the point charge e is moving by the Lorentz force and electric force, the equation of motion is
(Eq.51')
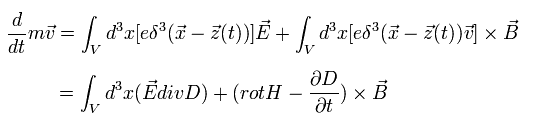
where we use the relation of Eq.24. And we interpret the charge's movement (= ev ) as the current i
But this interpretation is incorrect.
As shown on this page, the magnetic field around the moving single electron can always be expressed as the changing electric field.
The current i must be continuous. But the single electron is discontinuous.
And we can not count the same magnetic field twice.
Here we use the next relation
(Eq.52')
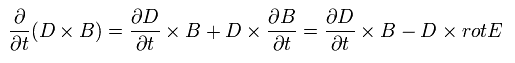
Substituting Eq.52' into Eq.51',
(Eq.53')
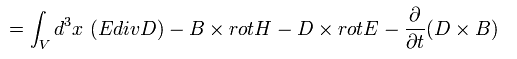
where A × B = - B × A.
And we define the momentums of the particle and the electromagnetic field, as follows,
(Eq.54')
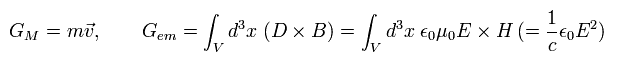
From Eq.52', Eq.53', and Eq.54', the equation of motion is
(Eq.55')
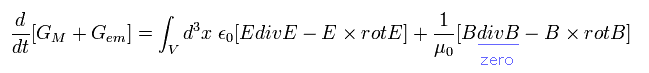
where we add B div B = 0.
From Eq.55', the x component of the force F (of electromagnetic field ) becomes
(Eq.56')
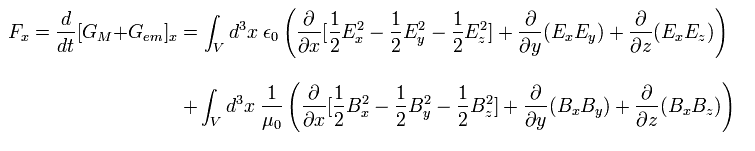
This is very important relation used in the relativistic energy momentum tensor.
But Eq.54' does NOT mean the electromagnetic field momentum, if the vacuum electric energy is not energy.
[ Lorentz invariant Maxwell's equations ]
Using the antisymmetric tensor, the x components of the electric and magnetic fields are
(Eq.57')
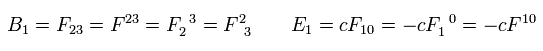
The antisymetric tensor satisfies the relations of
(Eq.58')
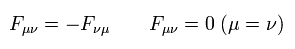
Using these relations, two of Maxwell's equations can be expressed as
(Eq.59')
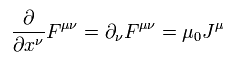
For example, when μ = 1,
(Eq.60')
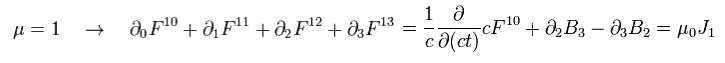
Using εμ = 1/c2 and Eq.57', Eq.60' proves to be equal to one of Maxwell's equations.
As I said, every variable (= x, A and J ) changes as four-vector, so Eq.59' changes as Lorentz-invariant tensor.
This means Maxwell equation of Eq.59' is Lorentz covariant (= "form" of Eq.59' doesn't change under Lorentz transformation.)
In Eq.59', contracting the two vectors ( ν is used twice, and they are a pair of contravariant and covariant vectors),
(Eq.61')
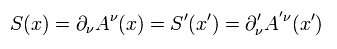
Eq.61' is Lorentz-invariant scalar.
And the next relation is satisfied.
(Eq.62')
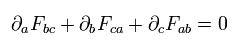
and
(Eq.63')
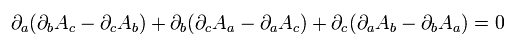
Eq.62' means the remaining Maxwell's equations. For example,
(Eq.64')
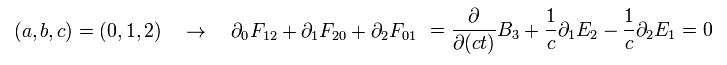
(Eq.65')
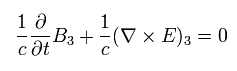
This is the last Maxwell equation. Of course, Eq.62' is Lorentz covariant tensor.
Next we define
(Eq.66')
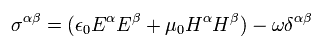
and
(Eq.67')
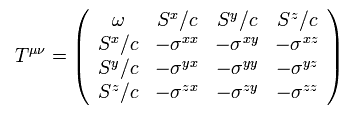
where ω and S mean vacuum energy and poynting vector.
Eq.67' means Lorentz covariant tensor, as follows,
(Eq.68')
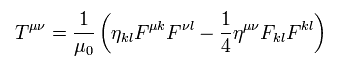
This is called energy momentum tensor of the electromagnetic field.
If we define the next relation
(Eq.69')
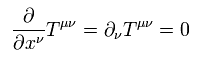
When μ = 0, Eq.69' is the same as the relation of energy and poyning vector.
And μ = 1, 2, or 3,
(Eq.70')
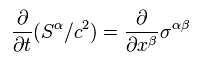
Eq.70' is the same as Eq.56' (= momentum and force ).
Probabley, they thought up the idea of the vector potential A to match Lorentz covariance.
Do you feel this intention in the definition of E using vector potential ?
General (special) relativity
Riemann, Ricci, Einstein tensors.

2012/5/22 updated. Feel free to link to this site.