四角形の重心を作図するのに、2通りの三角形の分割をせず、1通りの分割した三角形の重心
と面積比から作図できることをベクトルを用いて証明し、実際に作図することで、ベクトルに
興味をもち、有用性を感じることが、この教材のねらいである。
数学Aにある「埼玉県の重心」の続きで行うとよい。
なお、表記上、ベクトルは太字で表示する。

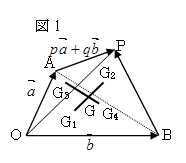
図1のような四角形OAPBに対して、基準とするベクトルを
OA=a,OB=b とすると、AP=pa+qb(p>0,q>0)とおけるので、
重心G,三角形OABの重心G1,三角形ABPの重心G2,
三角形OAPの重心G3,三角形OBPの重心G4に対して、
OG1=(1/3)a+(1/3)b,OG2=(1/3)(2+p)a+(1/3)(1+q)b
OG3=(1/3)(2+p)a+(1/3)qb,OG4=(1/3)(1+p)a+(1/3)(1+q)b となる。
四角形の重心Gは、線分G1G2と線分G3G4の交点になるので、
GG1:GG2=s:1-s , GG3:GG4=t:1-t とおくと、
OG=(1-s)OG1+sOG2=(1/3)(1+s+sp)a+(1/3)(1+sq)b
OG=(1-t)OG3+sOG4=(1/3)(2-t+p)a+(1/3)(t+q)b と表せる。
よって、1+s+sp=2-t+q
1+sq=t+q から t を消去すると、
2+s(p+q+1)=2+p+qより、s=(p+q)/(p+q+1)
ゆえに、GG1:GG2=s:1-s=(p+q)/(p+q+1):(p+q+1)-(p+q)/(p+q+1) =(p+q):1
となる。
一方、図2のように、三角形OABの面積をS1、三角形PABの面積をS2 とおいて、
面積比S1:S2を求める。∠AOB=θ ,∠BAP=φ とおくと、
S1=(1/2)|a||b|sinθ,S2=(1/2)|pa+qb||-a+b|sinφ

ここで、cosφ=(pa+qb)・(-a+b)/|pa+qb||-a+b| より、
cosφ=B/A とおくと、
A2={|pa+qb||-a+b|}2=|pa+qb|2|-a+b|2
=(p2|a|2+2pqa・b+q2|b|2)(|a|2-2a・b+|b|2)
=p2|a|4-4pq(a・b)2+q2|b|4-2p(p-q)|a|2a・b+2q(p-q)|b|2a・b+(p2+q2)|a|2|b|2
B2={(pa+qb)(-a+b)}2={(-p|a|2+(p-q)a・b+q|b|2)}2
=p2|a|4+(p-q)2(a・b)2+q2|b|4-2p(p-q)|a|2a・b+2q(p-q)|b|2a・b-2pq|a|2|b|2 から、
sin2φ=1-cos2φ=1-(B2/A2)=(1/A2)(A2-B2)=(1/A2){(p+q)2|a|2|b|2-(p+q)2(a・b)2}
={(p+q)2/A2}{|a|2|b|2-|a|2|b|2cos2θ}={(p+q)2|a|2|b|2/A2}sin2θ
よって、sinφ={(p+q)|a||b|/A}sinθ より、S2=(1/2)Asinφ=(1/2)(p+q)|a||b|sinθ=(p+q)S1
ゆえに、S1:S2=1:(p+q)となる。
これを利用して、GG1:GG2=(p+q):1となる点Gを決めればよい。
よって、三角形の分割を2通りしなくても、三角形OABと三角形PABの重心の位置を求め、
三角形OABと三角形PABの面積比を求めれば、四角形の重心の位置を求めることができる。