ベクトル方程式の点の存在範囲の問題を、アームが斜めに動くUFOキャッチャーを用いて
イメージすることから、ベクトル方程式の理解を深めることが、この教材のねらいである。
なお、表記上、ベクトルは太字で表示する。
ゲームセンターなどにあるUFOキャッチャーは、縦方向と横方向に動くアームがあり、
縦方向と横方向のボタンをそれぞれちょうどよい時間だけ押して、ちょうどよい距離を
動かすことができれば、そこにある景品(ぬいぐるみなど)を捕ることができる。
そこで、ここではアームが斜め2方向に動くスーパーUFOキャッチャーを考える。

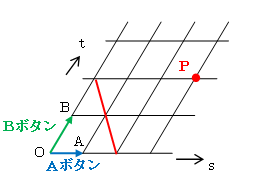
アームが図のように、Aボタンを押すとA方向に、
Bボタンを押すとB方向に、それぞれ1秒間に
矢印の長さだけ動くとする。
このとき、図の点Pにある景品を捕るには、
それぞれのボタンを何秒ずつ押せばよいかを考える。
答えは、Aボタンが3秒、Bボタンが2秒である。
これをベクトルで表すと、OP=3OA+2OBとなる。
また、図の赤線上にアームがいくための条件を考える。
Aボタンを押す時間を s 秒、Bボタンを押す時間を t 秒とすると。
答えは、s+t=2、すなわちAボタンとBボタンの押す時間の合計が2秒である。
これをベクトルで表すと、OP=sOA+tOBで、s+t=2 となる。
このような問題を通して、ベクトル方程式の点の存在範囲のイメージを深めるとよい。