フィボナッチ数やリュカ数といった興味深い数列を分析することで、数列に興味をもち、
一般項や漸化式に興味をもつことが、この教材のねらいである。
ある項が、その項の前の項と前の前の項を足した値になっている数列{an}:{1,1,2,3,5,8,13…}
のことをフィボナッチ数列という。
フィボナッチ数列は漸化式で表すと an+2=an+1+an(a1=a2=1)となるので、
フィボナッチ数列の一般項を、この三項間の漸化式を解いて求める。
まず、三項間の特性方程式 x2=x+1を解くと、x=(1±√5)/2 となる。
α=(1-√5)/2 ,β=(1+√5)/2 とおくと、
an+2-αan+1=β(an+1-αan) と変形できることから、
an+1-αan=βn-1(a2-αa1)=βn-1(1-α) となり、
ここで、1-α=1-(1-√5)/2=(1+√5)/2=βであるから、
an+1-αan=βn・・・①となる。
同様にαとβを入れ替えると、an+2-βan+1=α(an+1-βan) から、
an+1-βan=αn・・・②となる。
よって、①-②より、 (β-α)an=βn-αnとなり、
β-α=√5より、フィボナッチ数列の一般項は、
an=(1/√5)(βn-αn)=(1/√5){((1+√5)/2)n-((1-√5)/2)n} となる。ためしにnに値を1から順に代入して計算すると、a3=2,a4=3,a5=5,…となる。
ここで、β=(1+√5)/2について、1:βは黄金比であり、黄金比のn乗を順に求めていくと
面白い関係が見えてくる。、
β=(1+√5)/2,β2={(1+√5)/2}2=(3+√5)/2 ,β3={(1+√5)/2}3=(4+2√5)/2
以下同様に、β4=(7+3√5)/2, β5=(11+5√5)/2,…となり、
βn={(1+√5)/2}n=(xn+yn√5)/2 ・・③とおいたとき、
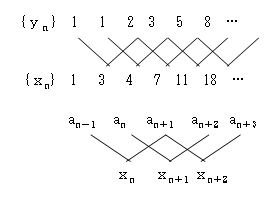
数列{xn}:{1,3,4,7,11,18}… と、数列{yn}:{1,1,2,3,5,8…} ができる。
αn=(xn-yn√5)/2 ・・④となるので、
an= (1/√5)(βn-αn)= (1/√5){((xn+yn√5)/2) -((xn-yn√5)/2)}=ynより、
数列{yn}はフィボナッチ数列であることがわかる。
また、数列{xn}:{1,3,4,7,11,18…}については、③+④よりxn=βn+αnという式が得られる。
ここで、zn+2=zn+1+zn(z1=1,z2=3)という数列を仮定して一般項を求めてみると、
zn+1-αzn=βn-1(z2-αz1)=βn-1(3-α) となり、
ここで、3-α=3-(1-√5)/2=(5+√5)/2=√5(√5+1)/2=√5β であるから、
zn+1-αzn=√5βn・・・⑤となる。
また、zn+1-βzn=αn-1(z2-βz1)=αn-1(3-β) となり、
3-β=3-(1+√5)/2=(5-√5)/2=√5(√5-1)/2=-√5α より、
zn+1-βzn=-√5αn・・・⑥となるから、
⑤-⑥より、 (β-α)an=√5(βn+αn) となり、zn=βn+αnとなる。
ゆえに数列{xn}も、xn+2=xn+1+xn(x1=1,x2=3)の関係を満たすことがわかる。
また、黄金比のn乗を別の視点から求めていくと、さらにおもしろい関係が見えてくる。
βは、2次方程式x2=x+1の解の1つであるから、β2=β+1の関係を満たすので、
βnを次のようにして求めることもできる。
β=(1+√5)/2,β2=1+1β=1+(1+√5)/2=(3+√5)/2,
β3=β(1+β)=β+β2=1+2β=(4+2√5)/2,同様にβ4=2+3β,β5=3+5β…より、
n≧2のとき、βn=an-1+anβ(an+1=an+an-1,a1=a2=1)
となることが推測される。これは数学的帰納法で証明できる。よって、
βn=an-1+(an(1+√5))/2=(2an-1+an+√5an)/2
=(2an-1+an+1-an-1+√5an)/2=(an+1+an-1+√5an)/2 となる。
ここで、βn=(xn+yn√5)/2 より、xn=an+1+an,yn=an (n≧2のとき)となる。
これを図で表してみると、下図のようになり、ynはフィボナッチ数列であり、
xnはフィボナッチ数列の隣の隣の項との和の数列となっていることがわかる。
数列{xn}のことをリュカ数という。

数列{xn}がxn+2=xn+1+xnの関係を満たして
いることは、右図を参考に計算すると、
xn+xn+1=(an-1+an+1)+(an+an+2)
=(an-1+an)+(an+1+an+2)
=an+1+an+3 =xn+2 となり、
示すことができる。