
トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは存在しない。
何が実在する素粒子なのか?
あなたがたは、テレビか何かで ヒッグスの”具体的な”イメージ画像などをご覧になったことがあるかもしれない。
基本的に 彼らは あなたがたに "リアル" でかつ "具体的な" ものを用いてヒッグスを紹介しようとするが、これは真実を語っていない。
例えば、ヒッグスとは 海のようなもので その中に 電子やクォークなどが "ふわふわ浮いている" のだろうか?
それとも ヒッグスは 何かの "抵抗" のようなもので、その中で 各粒子が自身の質量を感じることができるような存在なのだろうか?
しかし 実は、この問いの正解は 「ヒッグス粒子は単なる”数式 (= Math )”」なのである。
( 残念ながら 彼らは この真実をあなた方に伝えようとしない。)
(Fig.1) ヒッグスとは何か? 海? 抵抗? 単なる数式?

このページに、 ヒッグスの数学的な導出方法を示した。
ここでは どうしてヒッグスが標準模型にとって必要なのか簡潔に示す。
どうして 非常に”抽象的な”ヒッグスボソンの概念が生まれたのだろうか? この根本的な理由は 相対論にあると私は思う。
相対論的な制限は すべての理論のなかで 最も厳しいものである。
相対論によれば、すべてのものは 任意の速度の観測者から 同じように見えなければならない。
そのため、私たちは 具体的なイメージをあきらめて、非常に”抽象的な”数学に頼らなければならなくなった。
( しかし このページに示したように 相対論には 致命的な自己矛盾が存在する。)
これらの 非常に制限された条件の中で、彼らは ”ゲージ変換 + 対称性(= ゲージ不変性 )”に注目した。
( 残念ながら、これらは 単なる”数式の世界”であり、具体的なイメージがまったく存在しない。)
詳細は このページ の Eq.3 から Eq.29 を参照のこと。
(Eq.1) ディラックのラグランジアン (= 運動量項 + 質量項 )
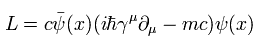
(Eq.2) ゲージ (= θ ) 変換
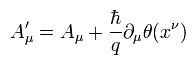
(Eq.3) マクスウェルのラグランジアンの 反対称テンソル Fμν は ゲージ変換で変化しない。
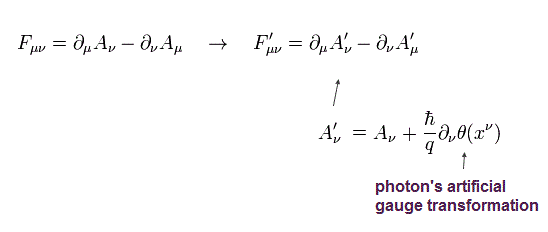
(Eq.4) マクスウェルのラグランジアン L は ゲージ変換で変化しない (= invariant)。
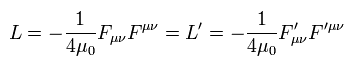
(Fig.2) 光子の ”質量項”(= mass term ) は ゲージ変換で変わってしまう。

Fig.2 に示したように、Eq.4 の 通常のマクスウェルのラグランジアンは Eq.2 を Eq.3 や Eq.4 に代入したとき 変化しない (= invariant)。
なぜなら、ゲージ θ が 打ち消されて消えるからである。
基本的に ゲージ θ は 非実在のものなので、表立って現れることは許されない。
しかし、もし このマクスウェルのラグランジアンが Fig.2 に示すように さらに 光子の質量項 (= mass term ) を含んでいるとしたら、Eq.2 を この質量項に代入したとき、この項は 不変ではない。
( そのため この場合は、ゲージが表に現れてしまう。つまり 質量項は ゲージ変換で 不変ではないということである。)
光子とグルーオンには 質量はない。そのため このやっかいな質量項を マクスウェルのラグランジアンに付け加える必要がない。
しかし 非常に重い W や Z ボソンにとっては深刻な問題である。(もちろん数学上の問題ではあるが・・)
この問題を解決するために、彼らは W、Z ボソンの質量をゼロとし、”対称性”を保ったまま それらに質量を与えるために ヒッグス場 という新たな概念を導入したのである。
また このページに示したように、左巻きと右巻きの電子やクォークはまったく別の概念のものである。( 1つは ”行列” で、もう1つは ”数”である。)
この奇妙な定義は β崩壊の非対称的な実験結果を基に導入したものである。
さらに アップクォーク、ダウンクォーク、電子、ニュートリノは 電弱統一理論においては 混ぜこぜになっている。
そのため それらの "定まった" 質量項を定義できないのである。
結果的に、電子やクォークにも 質量があってはならないことになる。そして、またしても ヒッグス機構に それらに質量を与える役目を任せたというわけである。
( あなたがたもお気づきのとおり、ここで最も重要な概念は ”質量項”+”ゲージ不変性(=対称性)”である。ただ これらは単なるルールにすぎない。)
”ヒッグスの風”? それとも ヒッグスは地球とともに動いているの?

後で説明するが、ヒッグスは クォーク、電子などのフェルミ粒子が動き回っているところと同じ場所に必ず存在していなければならない。
なぜなら、相対論的な場の量子論では、ヒッグス粒子とフェルミ粒子の相互作用項は それらの共通の変数 xμ を含んでいるからである。
そのため、例えば 原子核の内部のダウンクオークと同じ場所に 陽子の 125 倍もの 重いヒッグス粒子が常に存在しなければならない。
さて、どうして 原子核内部のクォークや 動き回っている電子などが この非常に重いヒッグス粒子に動きを妨げられないのだろうか?
非常に不合理な理論である。
”対称性”の理論では、電子やフェルミ粒子などは 対称性をキープするために 質量を持つことを禁止されているのである。
だから、ヒッグスが同一場所からなくなった瞬間、それらの質量はゼロになってしまう。
(これはルールなので、あなたがたが標準模型を信じているとしたら それに従う必要がある。)
あなたがたは、ヒッグスは不安定ですぐ消えるから、フェルミ粒子の動きを妨げないと思われるかもしれない。
しかし、実際には 真空には ヒッグス粒子があふれかえっているのである ( もちろん フェルミ粒子と同じ場所にも )
なぜなら ヒッグスのスカラー場は 次のようなヒッグス粒子 (= h ) の項も含んでいるからである。
ヒッグス粒子 (= h ) の項

加速器における ヒッグス粒子の生成について理解するには、最初に W、Z ボソンが 他の粒子とどのように相互作用するかを理解する必要がある。
通常のマクスウェル方程式を与える マクスウェルのラグランジアンは
(Eq.5) マクスウェルのラグランジアン (= "数" )

このページに示したように、W ボソンのラグランジアンは マクスウェルのよりも複雑である。
もちろん、1つが "数"、もう片方が "行列" であることを除けば、それらは似ているが。
”行列”に頼らなければならないという事実は すなわちこれらの理論が リアリティーのない 単なる "数学上" の概念であることを示している。
(Eq.6) ウィークボソンのラグランジアン (= "2 × 2 行列" )

ウィークボソンの反対称テンソル Fμν は、
(Eq.7)
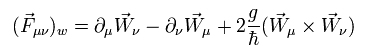
例えば、Eq.7 の "1" 成分は、
(Eq.8)

Eq.7 (Eq.8) の全成分を Eq.6 のラグランジアンに代入すると、ウィーク、Z ボソンにおける様様な相互作用項を得ることができる。
電弱統一理論では、W ボソンの 1-3 成分と、Bの場を W±、 Z ボソン、 光子 (= A ) に置き換える。
( このページの Eq.61 から Eq.65 を参照のこと。 )
(Eq.9) W± ボソンへの変換
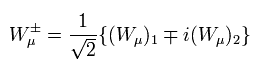
(Eq.10) Z、 A ボソンへの統合と変換。
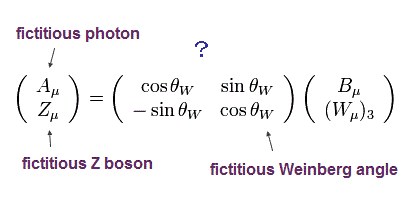
この理論では、 W±、 Z、 A ボソン を 次のラグランジアンの B と 3種類の W ボソンに代入して置き換える。
(Eq.11)

Eq.11 から得られる項の一部は、
(Eq.12) W ボソン と A (= 光子 ) の相互作用項

(Eq.13) W と Z ボソンの相互作用項。

ファインマンダイアグラムを用いると、 Eq.12 と Eq.13 の相互作用項は次のように表せる。
(Fig.3) W、 Z、 A ボソンの相互作用項のファインマンダイアグラム。

相対論的な 場の量子論 や QED は、粒子間の相互作用を考慮するとき、相互作用項とファインマンダイアグラムが 使うことのできるツールのすべてである。
そのため 場の量子論では これらのような 非常に抽象的かつ制限された "数学的な" 道具しか使うことができないのである。
( このことが、現在の相対論的な場の量子論 と 素粒子物理学において ”リアリティー”がなくなってしまった主要な要因である。)
Eq.12 の相互作用を用いて、加速器は 電子+陽電子 → 光子 (= A ) → WW ボソン のようにして W ボソンのペアを理論的に生成することができる。
もちろん、W ボソンは 直接観察することができないため、この解釈は 完全に標準模型に依存していることはいうまでもない。
Eq.11 の 他の項は、
(Eq.14) W ボソン同士の相互作用項

(Eq.15) WW と ZZ ボソンの相互作用項

(Eq.16) WW と ZA ボソンの相互作用項

(Eq.17) WW と AA ボソンの相互作用項

これらの様様な相互作用項を組み合わせれば、いろんな相互作用パターンを考えることができる。
そのため、これらの過程のうちのたった1つのみで ポジティブな結果が出たとしても、それをそう簡単に信じてはならないと思われる。
( なぜなら、直接観測できない 中間の粒子が 単なる”幻”である可能性もあるからである。)
このページ ( Eq.86- Eq.102 )に示したように、次の ヒッグス場 (= h(x) ) を用いる。
(Eq.18)
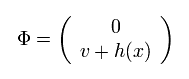
ここで "v" は 真空の定数で h(x) は ヒッグスボソンである。
ちなみに このパラメーター "v" は 標準模型そのものから導くことはできず、実験から決めるしかない。
すると、次の項を得ることができた。
(Eq.19)
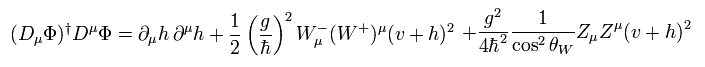
Eq.19 では、 W、Z ボソンの 質量項 ( × 1/2 ) は、
(Eq.20)
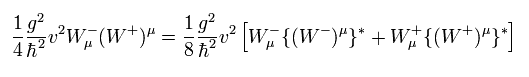
と
(Eq.21)
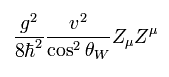
Eq.10 の定義と、Eq.18 の上部の成分がゼロであることを考慮すると、Eq.19 の ヒッグス場には 光子 (= A ) の質量項が現れない。
これは重要である。しかし ちょっと人為的なトリックのように思えるが・・・。
Eq.19 の他の項は 次を含んでいる。
(Eq.22) W、Z ボソン と ヒッグスの相互作用項

E.22 のいくつかの項は 次のように表せる。
(Fig.4) W、 Z ボソン と ヒッグスの相互作用項のダイアグラム

Fig.4 の相互作用は 加速器における WW、ZZ チャンネル における崩壊モードを示している。
もちろん、私たちは これら W、Z、ヒッグスなどの中間の粒子を直接観測することはできない。
これらの実在性は 完全に標準模型に依存している。
(よって、もし 標準模型が変わってしまうと、これらの解釈が変わってしまう。)
例えば、実験では 電子、電磁波、ニュートリノなどの最終生成物の動きを解析するだけである。
( W、Z、ヒッグスは見ていない。)
標準模型によれば、もしヒッグスが存在しないと、電子、クォークなどのすべてのフェルミ粒子の質量がゼロになってしまうため、この世のすべてのものは 壊れてしまうことになる。
ウィークボソンのように、フェルミ粒子とヒッグス間の新たな相互作用ラグランジアンを導入する必要がある。
例えば、クォークの質量を生成するラグランジアンは、
(Eq.23) クォークとヒッグスのラグランジアン

ここでは 真空は、
(Eq.24)

Eq.23 の uL と dL は それぞれ "左巻きのアップクォーク" と "左巻きのダウンクォーク" である。
重要な点は Eq.23 と Eq.24 は 単なる "定義" (= ルール ) であり、自然に得られたものではないということである。
Eq.24 を Eq.23 に代入すると、次を得る。
(Eq.25)

ここで
(Eq.26)

md と mu は ダウンとアップクォークの質量である。
Eq.25 の最初の行は ダウンとアップクォークの質量項を意味している。
また Eq.25 の 2行目は ヒッグス (= h ) とクォークの相互作用項を意味している。
そのため これらの相互作用の強さは それらの質量に関係していることになる。
しかし Eq.23 でそうなるようなラグランジアンを定義したので、この結果はあたりまえのものである。
"無限" かつ "非常に重い" ヒッグス粒子が実在するのか ? それとも 単なる”幻想”か?

もし、フェルミ粒子とヒッグスの相互作用が それらの質量(= 抵抗 )を引き起こすと考えると、ヒッグスは フェルミ粒子が動きまわるところすべてに存在する必要がある。
どのように これら 陽子の約 125 倍もの 重いヒッグス粒子が フェルミ粒子の進行方向を妨げることなく 相互作用し続けることができるのだろうか?
非常に奇妙としか言いようがない。
標準模型は クォークの質量を予測することはできない。
そのため、私たちは 真空の値 " v " と 定数 cd、 cu などの値を実験のみから得るしかないのである。
この何も予測できない点が 標準模型のウイークポイントである。
ファインマンダイアグラムを使用すると、Eq.25 は 次のように表せる。
(Fig.5) ”クォーク”と”ヒッグスボソン”の相互作用のファンマンダイアグラム。

Fig.5 も 加速器においては 重要な過程の1つである。
しかし、何度もいうように これらのクォークやヒッグスは直接観測できるものではない。
( この解釈は 標準模型に依存している。)
このページ ( Eq.103- Eq.109 )で、 グルーオン (= G ) と フェルミ粒子 (= quarks, ψ ) の相互作用項を得ることができた。
(Eq.27) グルーオンとクォークの相互作用

Eq.27 のファインマンダイアグラムは、
(Fig.5) "クォーク" (= q ) と "グルーオン" (= G ) の相互作用

グルーオンは質量がないため、対称性を保つために ヒッグス機構を使用する必要がない。
つまり、グルーオンとヒッグスの間の相互作用項が存在しないということである。
Fig.5 の過程は 陽子 - 陽子 衝突 の加速器などで 重要である。
なぜなら 標準模型によれば、陽子のほとんどのエネルギー (= 質量 ) は グルーオンの結合エネルギーによるものだからである。
もちろん、標準模型が間違いならば、この解釈は使うことができない。
アインシュタインの質量とエネルギーの関係式によれば、すべての質量のエネルギーは mc2 になる。
それなのに、どうして このグルーオンエネルギー (= 陽子の質量 ) がヒッグスと何の関係もないのだろうか?
質量というものはすべてに共通の概念ではないのか?
あなたがたは、この陽子の質量 (= グルーオン) と 他のフェルミ粒子の質量の違いに 何か 人為的な”トリック”を感じないだろうか?
これらの相互作用項を組み合わせると、非常にたくさんの種類の ヒッグスの生成崩壊過程を考えることができる。
つまり 正確にいえば、これらすべての反応パターン を実験で確認する必要がある。
しかし、彼らは これらのうちのほんの1つでも ポジティブな結果がでれば ヒッグスの存在確認に 十分だと考えているような気がする。これも奇妙である。
さらに、標準模型が 標準模型そのものから得ることのできない 多くの パラメーターを含んでいる。
このページ ( Eq.47 と Eq.72 )から、 フェルミ粒子、光子 (= A )、W ボソン間の相互作用を考えることができる。
(Fig.6) フェルミ粒子、W ボソン、光子間の相互作用のファインマンダイアグラム

荷電粒子と光子間の相互作用項は もとのディラックのラグランジアンにも存在していた。
また、ベータ崩壊によれば、ウィークボソンは クォーク、電子、ニュートリノなどのフェルミ粒子と相互作用することができる。
Fig.6 は 電子 (e-) と 陽電子 (e+) 衝突を使用する加速器において重要である。
(Fig.7) ヒッグスの γγ 崩壊モード

Fig.7 は 陽子 - 陽子 衝突 → ヒッグス → 2光子 (= γ線 ) の崩壊過程の1例である。
もちろん、上のセクションで示したとおり、この中間の過程にはたくさんの種類のパターンが存在する。
Fig.7 は それらのうちの1つにすぎない。
(Fig.8) 陽子、反陽子衝突によるヒッグス生成

Fig.8 は 粒子、反粒子衝突がヒッグスを生じさせるパターンの1例である。
しかし、クォーク、ヒッグス、W ボソンは 実際に取り出して、直接観察できるものではない。
そのため、最終産物を観察して この過程が正しいことを信じるしかないのである。
( クォークは単離することができないので、他の粒子と結合した”ジェット”を観察するしかない。)
あなたがたは よくニュースなどで、「ヒッグスが見つかった確率は 99 % とか何か」などという文句を聞かないだろうか?
重要な点は どのようにヒッグスなしのバックグラウンドの状態を決定するかということである。
なぜなら、ヒッグスの存在は 推定される ヒッグスなしの状態との比較によって判断するからである。
このヒッグスなしのバックグラウンドは 様々なエネルギー状態のバックグラウンドから推定するしかない。
もちろん、このヒッグスなしの状態の決定にミスがあれば、実験結果の解釈は全然別のものになってしまう。
無数の衝突のうちほんの少ししかヒッグスの可能性のある粒子が生成されない中で、これらを区別、判断することは非常に困難な作業である。
”神の粒子”ヒッグスが見つかったと報告したニュースの後、おそらく あなた方は ヒッグス粒子とその性質についてもっと知りたくて質問などされたかもしれない。
私が 様々なインターネット上のブログや掲示板など見ていると、これらの質問に対する回答は 恐ろしいくらい曖昧である。
これらを見ていると、現在の科学は永遠に この曖昧かつ抽象的な数式だけの世界から抜け出せないんじゃないかと不安になってくる。
例えば、次のようなことが知りたくなるだろう。
”すべてのフェルミ粒子、W、Z ボソンには質量がない。それらの質量は それらの周囲のヒッグス場の真空との相互作用によるものである。”
”では なぜ光子(=電磁波)やグルーオンは それら無限のヒッグス場の存在をまったく感じることができないのだろうか?”
”重力は”グラビトン”の交換によって生じる。それなら、このグラビトンは フェルミ粒子や W, Z ボソンを直接感じるのではなく、代わりに その周囲のヒッグス場を察知するということだろうか?”
これらは思い浮かべることが非常に困難である。どうやって その違いを正確に区別しているのだろうか?
(Fig.9) ”重力”と 質量 の本当の関係は何なのだろうか?

Fig.9 に示したように、”非常に賢い”グラビトン (= graviton ) は 電子、Wボソン、陽子、光子の違いを正確に区別できるということか?
なぜなら 電子やWボソンの場合、グラビトンは 電子などに直接作用するのではなく その周囲の ヒッグス場に作用するからである。
しかし 陽子 (=proton ) の場合、グラビトンは 陽子そのものに作用する。
さらに、一般相対論によれば、光子(=電磁波 ) の進行方向が 重力によって曲げられる。
しかし 光子には質量がない。どうやって この”非常に賢い” グラビトンは それらの違いを区別することができるのだろうか??
お気づきのとおり、この標準模型の理論は 非常に不自然なものなのである。
(Fig.10) ”真空”とは何か → 何もなし (= Nothing ) ? ”無限の”粒子?

ご存じのとおり、特殊相対論によれば、”エーテル”(= Aether ) が禁止されている。これはつまり 真空には 何もない (= Nothing ) ということになる。
( しかし このページに示したように 相対論には 致命的な自己矛盾が存在する。)
奇妙なことに、特殊相対論と量子論を組み合わせた 相対論的な場の量子論 (= relativistic QFT ) によれば、真空には 無限かつ多くの種類の粒子が含まれていなければならない。
つまり状況がさらに悪化しているのである。
結果的に 相対論的な場の量子論は 相対論に依存していながら 特殊相対論を完全に無視していることになる。
あなたがたは ヒッグスの発見のニュースをお聞きになったかもしれないが、ヒッグスが絡んでいる 質量というのは すべてのうちの ほんの 2 % を占めるにすぎない。
すべての質量のうち 98 % は 量子色力学 (= QCD ) によって生じるとされている。
QCD と "多世界様の"経路積分によれば、クォークと反クォークの無限のペアが 常に グルーオンを介して 真空中に 生成、消滅していなければならない。
これら グルーオンを介した 凝集が 陽子などの 質量の 98 % を占めているとされている。
しかし 例えば 電子はグルーオンとの関係はまったくない。そのため ヒッグス機構も 標準模型と QCD にとって 必要不可欠なのである。
あたながたは これらの理論がちょっとうまく できすぎていると思われないだろうか?
彼らは いわゆる”エーテル”の風を否定したが、これらの場の量子論の真空中の無限の粒子は エーテルのように "風" を引き起こさないのだろうか?
これら無限の奇妙かつ非現実的な粒子に依存するよりも 地球とともに動いているエーテルを認めるほうが より自然でしっくりくる。
(Eq.28) ヒッグス場の真空
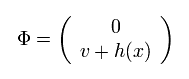
(Eq.29) フェルミ粒子の質量

Eq.28 や Eq.29 に示したように、フェルミ粒子の質量は 真空の値 "v" によって生じる。
これはつまり、ヒッグス機構は それらに質量を与える 一種の "エーテル" なるものを使用しているのである。
しかし 彼らはこの事実をかたくなに認めようとしない。なぜなのだろうか?
よって、この真空値 "v" は エーテルの風のごとく ”風”を引き起こすのだろうか?
もちろん、この機構は ヒッグスの運動量項と質量項を含む スカラーの式とリンクしている。
もし、ヒッグスと ヒッグスとの相互作用項が あらゆる場所に存在していなかったとしたら、私たちは 加速器で ヒッグス粒子を生成できないことになる。
また 新たな W ボソンや 電子、陽電子ペアを実験で生成させようとするとき、それらに質量を与えるために ヒッグス粒子がそれらと同一地点に存在する必要がある。
すると、これら非常に重いヒッグス粒子が フェルミ粒子の進行方向を妨げたりしないのだろうか?
また QCD の "無限の"粒子も それらの進行方向を妨げたりしないのだろうか?
あなたがたは これらの理論が いわゆるエーテル理論よりも さらに不自然だと思われないだろうか?
もし、あなたがたがこれらのことを インターネット上のブログや掲示板で質問したとしたら、彼らはおそらく これらの質問にはっきり回答できないだろう。
なぜなら 何度もいうように これら標準模型や QFT は ”非実在” かつ 単なる”数式上の”世界のものだからである。 (= "Shut up and calculate !" 状態である。).
ボーアとアインシュタインの論争に見られるように、アインシュタインは生涯、これらの奇妙な量子論を認めなかった。
しかし 一方で アインシュタインは ボーア模型とドブロイ理論を認めていた。
彼は ボーア模型が ヘリウムイオン (= He+ ) においても成り立つことを知ると、「なら ボーア模型は正しいに違いない。」と言ったそうである。

2012/7/4 updated This site is link free.