
トップページ (正確な新ボーア模型)
電子スピンは実在しない。
ローレンツ変換は間違い?
(Fig.1) 特殊相対論は 致命的なパラドックスを引き起こす。

最近の興味深い論文 ( M. Mansuripur 著、 ここ, arxiv, ニュース参照 ) によれば、 ローレンツ力 が 特殊相対性理論と矛盾するらしい。
静止した観測者 (= S ) の視点からは、 中性の電線回路が 電場 E の中で 静止している。
しかし 動いている観測者 (= S' ) からは、この電線の上下の部分が 正電荷、負電荷に帯電してしまい、結果 電場によって 回転してしまうことになる。
これは 明らかにパラドックスであり、特殊相対論の 欠陥を露呈している。
(Fig.1') 特殊相対論は ローレンツ力で破綻している。

もしこの論文が正しいと、量子電磁力学、標準模型 ( ゲージ対称性に依存 ) などの理論が
破綻してしまう。
そのため、彼の論文は このサイトにあるように 非常に多くの反対意見を招いてしまった。
結論から先に言うと、 Mansuripur が主張するように、特殊相対論は 電磁気学で 破綻している。
様々な反対論文 ( ここ、ここ、ここ ) などを見る限り、彼らの解決策は リアルでない "偽の" 回転中心なるものに依存しており、到底 正常な解決策とは呼べないものばかりである。
(Fig.2) ローレンツ変換 → 新たな電荷 (= ρ'e ) が 発生する。 ↓
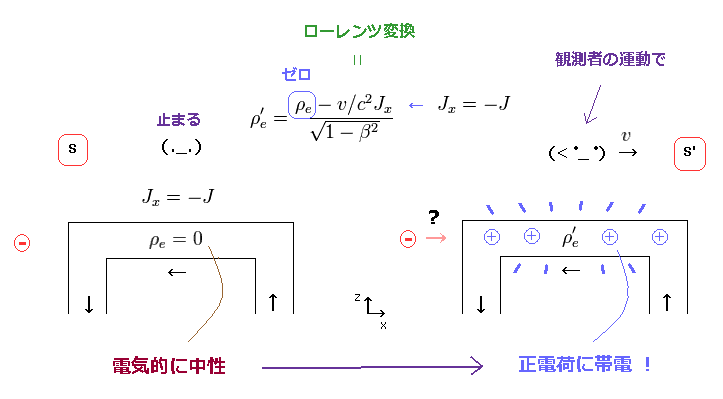
この論文は このページに示したような、電磁場のローレンツ変換における欠陥を ついている。
特殊相対論によれば、 電荷密度 (= ρe ) と 電流密度 (= J ) は ローレンツ変換の下で 時空間座標 (= ct, x, y, z ) のように 変換する。 ここ (p.16)、 ここ (p.3) など参照のこと。
Fig.2 左では、電線は 電気的に中性である (= S 系 )。
しかし 観測者が 動きだした瞬間に 奇妙な"正電荷"が 電線内に 生成されてしまう (= Fig.2 右、 S' 系 )。
結果的に、外にある荷電粒子 (= ここでは負電荷 ) が S' 系でのみ 電線の方向へ 引き付けられてしまうことになる。
これは明らかに 相対論における致命的な パラドックスである。
(Fig.3) ローレンツ変換。

基本的に 電荷 (= ρ ) と 電流 (= J ) 密度は マクスウェル方程式を満たすために Fig.3 のように変換される必要がある。
この Fig.3 の変換こそが パラドックスを引き起こす根源である。
(Fig.4) 特殊相対論は ローレンツ力で 破綻している。

これらの論文では、 電流 J が 流れる 四角の電線回路を使用している。
この電線は 同数の正電荷と負電荷を含んでおり、電気的に 中性になっている。
外電場 E は x 方向を向いている。
この電線は 電気的に中性であるため、S 系では 電場によって 回転 しない。
(Fig.5) 観測者の運動 (= S' ) で、 電線上部が正電荷、電線下部が負電荷に帯電する。

S 系では、観測者は静止しており、中性の電線のため 電荷密度はゼロ ( ρ = 0 ) である。
上部の電線の電流は "-J" であり、下部電線内の電流は +J である。
S' 系では、観測者が x 方向に 速度 V で動いている。
ρ=0 と Jx = -J を Fig.3 のローレンツ変換に代入して、S' 系では 上部の電線は 正電荷に帯電してしまうことが分かる。
一方、ρ=0 と Jx = J を Fig.3 に代入して、下部の電線は S' 系では 負電荷に帯電する。
(Fig.6) 電場 E の下で 上部の正の電線が右に、下部の負の電線が 左に移動する。

結果的に S' 系では、電場 E の下で 上部の ( 正 ) の電線は 右方向に、 下部の ( 負 ) の電線は 左方向に動いてしまい、すなわち 電線全体が 時計回り方向に 回転してしまうことになる。
S 系では、この電線は 中性であるため、回転しないのにである。
これは 明らかにパラドックスである。
なぜなら この観測者は 対象に触れずして 単なる単純移動 (= S' ) のみで 電線全体を回転することができるからである。
残念ながら、この致命的なパラドックスには 解決策は 何も 存在しない。
(Fig.7) トルク ( N ) = 回転半径 (= r ) × 力 (= F )。
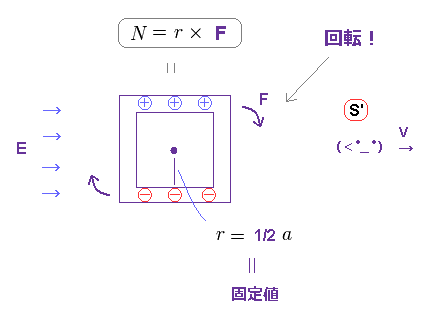
トルク (= N ) は 力のモーメントであり、これにより、角運動量 L が変化する。
このトルクは 半径 × 力 ( N = r × F ) で表される。
Fig.6 に示したように、上下部の電線に新たに発生した奇妙な電荷に 電場 E が作用することによって、 S' 系でのみ、回転トルクが 発生することになる。
(Fig.8) "偽の" 回転中心が 解決には必要 ?

Fig.6 のパラドックスを解決するのに、彼らは "仮想"の回転中心を設定した。
この仮想の中心は 動いている観測者の地点に存在するらしい。
そして "P" が 所謂 隠れた運動量 (= hidden momentum ) であり、 人為的な概念である。
もちろん、この仮想の中心は Fig.7 の本当の回転中心とは 何の関係もない。
(Fig.9) トルクの中身を"すり替える"のに 人為的なトリックを使用。

このサイトにあるように、トルク (= N、力のモーメント ) は 角運動量 (= L ) の時間微分で与えられる。
Fig.9 上 (= 1 ) では、S' 系で、電場 E が 電線全体を回転させている (= Fig.6,7 ).
回転を止める解決法として、彼らは Fig.9 下に示すように トルクの意味を 完全に 別のもの (= N = 半径の時間微分 × 運動量 ) に 取り換えてしまった。
しかし これらの解決策 ( ここ, ここ ) では、動く観測者の地点に "架空の" 回転中心を 設定する必要がでてくる。
もちろん、この観測者のところに リアルな回転中心は 存在しない。
さらに、この運動量 P も 架空の 隠れた運動量というものである。
これら 架空の回転中心と運動量に頼るということは、 Mansuripur のパラドックスは 全然解決されていない ということである。
(Fig.10) トルクは 半径 (= r ) の時間微分 × 定数 P ?

彼らは Fig.9 に示したように、トルクの本来の定義 ( N = r × P ) を まったく別の物に すり替えてしまった。
さらに、観測者と伴に 速度 V で動く 架空の回転中心なるものを こしらえてしまった。
架空の半径 ( r = Vt ) の時間微分は "V" のため、このトルク (?) は V × P (= 隠れた運動量 ) に等しくなると 彼らは主張しているのである。
この人為的な定義が正しいとすると、観測者は 対象物に触れずして、単なる等速運動のみで、角運動量を増加させることが可能になってしまう。
つまり この考えは 物理の基本的な原理に 完全に違反していることになる。
(Fig.11) 回転の仮想の中心は 本当の解決策でない。

結果的に、ローレンツ力のパラドックスは 解決されていない。
仮想の回転中心は 本来のトルクとは 何の 関係もない。
なぜなら、観測者 (= 仮想中心 ) は 電線回路と 何かの力や紐などで 繋がってはいないからである。
これらの本当のパラドックスに対する解決策は 間違った人為的な定義に基づいている。
正しい解決策は 物理の基本ルールに従わなければならないことは言うまでもない。
(Fig.12) ローレンツ力のパラドックス。 ↓

このセクションでは、新たに発生した電荷や、電場 E によるトルクの値を計算していく。
そして、様々な論文にあるように、元のトルクが V × 隠れた運動量 P に
偶然に一致することを示す。
この隠れた運動量も 偽の運動量であり、
間違った定義に基づいている。
よって、ローレンツ力のパラドックスは 全然解決されていないのである。
(Fig.13) 中性の電線が 静止した観測者 (= S ) の視点では 静止している。

静止した観測者 (= S 系 ) からの視点では、中性の電線回路 (= 四角形、一辺の長さが "a" ) は 電場 E の中で 静止している。
この電線は x-y 平面上にあり、電場 E は x 方向を向いている。
電線の上部 (下部) を流れる電流は -x ( x ) 方向である。
(Fig.14) 磁気モーメント μ = 電流 I × a2.

マクスウェルの法則によれば、ループ状の電流は 磁気双極子モーメント(= μ ) を生じる。
この 磁気モーメントは 電流 I と そのループ内の面積 S の積で表わされる。
この場合では 面積は S = a2 であるため、 磁気モーメントは μ = Ia2 となる。
(Fig.15) 観測者の運動で 新たな正と負の電荷が 発生する?

電荷 (= ρ ) と 電流 (= J ) 密度のローレンツ変換によれば、本来は中性の電線 (= S ) から、新たな電荷が 動く観測者の系 (= S' ) において 発生してしまうことになる。
電線のループの上下部には 互いに 逆方向の電流が流れている。
そのため、S' 系で生じた電荷は 上部の電線では 正 で、下部の電線では 負 になる。
(Fig.16) S 系で静止する電線が S' 系で回転する ? ← パラドックス。

結果として、この中性の電線は S 系で静止しているにもかからわず、 新たに発生した電荷によって S' 系でのみ 回転してしまうことになる。
これは 明らかに 相対論の致命的なパラドックスである。ρ' は S' 系における 電荷 ( 線 )密度 である。
(Fig.17) 電線全体に対するトルク。

上下部の各電線に含まれる全電荷量は 電荷密度 (= ρ' ) × ( ローレンツ収縮した ) 電線の長さ で与えられる。
結果的に 各電線内の全電荷量は ±VJa/c2 になる。
(Fig.18)

電気力 F は 全電荷量 × 電場 E で与えられる。
上下部の電線は 逆電荷を持つため、電線全体は S' 系でのみ 回転してしまうことになる。
(Fig.19) 電線全体に対するトルクは F × 半径。

互いに逆方向に働く 電気力 F によって この電線全体に 回転トルク (= N ) が発生する。
このトルク N は 力 F × 中心からの距離 (= 1/2 a ) で 与えられる。
(Fig.20) 電線に作用する 全トルク (= N )。

正電荷、負電荷に作用するトルクを足して ( 1/2a × 2 = a )、計算結果は Fig.19.20 に示したようになる ( Fig.14 の磁気モーメント μ を用いて )。
(Fig.21) トルク (= N ) が 角運動量 (= L ) を増加させる。

Fig.19 にあるように、トルク (= N ) は 角運動量 (= L ) を増加させる。
Fig.16,17 では、 回転中心と 力の作用点の距離 (= r = 1/2a ) は定数値 である。
そのため、このトルクによって 回転の速度が 増加することになる。
(Fig.22) トルク = 角運動量 (= L ) の時間微分。

トルク (= N ) は 角運動量 (= L ) の時間微分で与えられる。
このケースでは、半径 r は 固定値 (= 1/2a ) である。
つまり トルクは r × F (= 力 ) という 本来の形式で与えられる。
(Fig.23) ↓ これは リアルなトルクなのか ?

すでに述べたように、トルク N は 角運動量の時間微分で与えられる。
しかし 彼らは 運動量 (= P ) の代わりに 半径 ( r = Vt ) のほうを変化 (= 微分 ) させた。
これは 明らかに 間違ったトリックである。
Fig.16 や Fig.17 をみて分かるように、回転半径は このケースでは 固定された値である ( r= 1/2a )。
つまり 正しい答えでは、半径の時間微分は ゼロになる。
(Fig.24) これは本当にトルクなのか ?

Fig.24 に示したように、運動量 P が 変化しなくても、 増加した半径 (= r ) によって トルクは生じるとしている。
なぜなら 半径が増加するにつれて 角運動量 (= r × P ) が 増加するからである。
(Fig.25) 正常なトルク。

電線の1辺の長さは "a" である。
そのため 回転半径 r = 1/a は "固定値" である。
(Fig.26) "架空の"回転中心が このパラドックスの解決に必要不可欠。

Fig.23 のトリックを使用して、彼らは Fig.26 のように トルクの本来の意味を 人為的にすり替えてしまった。
問題は 移動する観測者の地点に 架空の回転中心を こしらえてしまったことである。
結果的に この半径は r = Vt ( V は 観測者の速度 ) のように変化する。
そのため、このトルクは N = V × P で与えられ、ゼロにならないということになる。
(Fig.27) しかし 回転中心自体が 幻想である。

しかし お気づきのとおり、この回転中心に リアリティーはなく、電場によって生じる本来のトルクとは 何の関係もない。
同じ速度で運動する観測者が "リアルな"トルクを引き起こすことは 不可能である。
なぜなら この観測者は 電線回路に 力か紐などで まったく 繋がっていないからである。
S' 系で、電線回路に作用するのは 電気力のみしか存在しない。
そのため 何か他の外力が ない限り、本当のトルクは キャンセルされることは なく、つまり このパラドックスは 解決できないことになる。
(Fig.28) 電線内の正の電線が 電場 E で加速される?

このページでは、正電荷が電流として流れ、負電荷が 静止しているとする。
この 電流 J は J = ρv で与えられ、 ρ は 正電荷の 電荷密度で、 "v" は 電線内での これらの電荷の速度である。
隠れた運動量の計算では、これら正電荷が 電線内でも 電場によって 加速されるとしている。
そのため 右側の電線内の電荷は 左側の電線内よりも より多くの運動量 ( +ρEa ) を得ることになる。
(Fig.29) 相対論的な運動量 P と エネルギー T。

相対論的な 運動量 (= P ) と エネルギー (= T ) は Fig.29 で与えられる。 このページ参照のこと。
エネルギー T に v/c2 を掛けると、運動量 P が得られる。
(Fig.30) 右電線内の電荷が得た運動量 (= ΔP ) ?

1辺の長さが "a" であることを考慮すると、右電線内の電荷が得た全エネルギー (= ΔT ) は (ρEa)a に等しくなる。
Fig.29 から、得た全運動量 (= ΔP ) は Fig.30 で与えられる。
右側の電線内に 余剰の運動量が含まれることになり、これを 隠れた運動量と見なしたわけである。
しかし、実際には 全運動量の合計は ゼロになり、隠れた運動量も 存在しないことになる。
(Fig.31) 電流 J は 左右の電線内で同じ値である。

電線の回路では、電流 J は 必ず 一様でなくてはならず、そうでないと、どこかに電流が溜まってしまうことになる。
そのため、たとえ 電荷が運動エネルギーを得て 各運動量が増加したとしても、一定の電流 J を保つために それらの電荷密度 (= ρ ) は 減少しなければならない。
(Fig.32) 左右の電線内の 全運動量は同じである。

もし 電流 J が 必ず同じ値であるとすると、左右の電線の全運動量も Fig.32 に示すように 必ず 同じになる必要がある。
なぜなら 各運動量の増加分は それらの電荷密度の減少分で キャンセルされるからである。
(Fig.33) 電線ループの 隠れた運動量?

Fig.31,32 の事実を無視して、彼らは Fig.30 から この電線の 全運動量 (= ΔP ) を計算した。
Fig.14 の磁気モーメント μ = Ia2 の定義を用いて、Fig.20 の結果を得た。
(Fig.34) 偶然の一致 ?

偶然にも 完全に 異なった概念に基づく トルクの計算結果が完全に一致してしまうことになる。
Fig.20 のトルクは 半径 × 力 F で与えられ、その形式は 通常の形をしている。
Fig.27 の 架空の中心とFig.33 の隠れた運動量を用いて、Fig.20 と同じ結果を得ることができた。
これらの 人為的なトリックは 通常のトルクと同じ値を得るためだけに導入されたことは 明白である。
(Fig.35)

Fig.29 と Fig.30 を用いた運動量の計算もおかしい。
ΔP は 全運動量の ほんの一部にすぎない。
そのため 電流の全速度 "v" を この ΔP にあてがうことはできない。
( この ΔP は その速度の ほんの一部を与えるだけである。 )
(Fig.36) 各電荷は 自由粒子ではない。

Fig.28 では、運動エネルギーの計算のとき、電流を 自由粒子として扱った。
しかし 電流が一様ということは、各電荷は互いに独立状態ではない ( Fig.36 参照 )。
Fig.33 の運動量は正しくない。
もし 電流内の これらの正電荷が x 方向に流れるときに エネルギーを得るとしたら、これらの電荷は 電線全体を x 方向に プッシュすることになる。
( この押す力は エネルギーの差から x 方向のほうが -x 方向よりも強い。)
(Fig.37)

しかし 実際には 電線内の負電荷が 電場によって逆方向に引っ張られるため この正電荷のエネルギーをキャンセルすることになる。
なぜなら 電線内の負電荷と正電荷は互いに引き合っているからである。
(Fig.38) S 系での トルク = 0 からスタート。

この論文は Fig.33 の隠れた運動量を得るための 別の方法を導入している。
S 系では、外磁場 B は ゼロである。
つまり 磁気モーメント μ を持つ電線全体に対する全トルクは ゼロになる ( μ × B = 0 )。
ローレンツ変換の下で、 μ×B の関係は Fig.38 右のように変化する。
彼らは μE/c2 の部分を 隠れた運動量として定義した。
もちろん、この隠れた運動量は 実在のものではない。
(Fig.39) 電磁場のローレンツ変換。

電磁場のローレンツ変換は Fig.39 のようになる。
電場 E は 観測者の速度に平行であるため、磁場 B は 外積のため 必ず
ゼロになる。
つまり トルク = 0 の前提条件からスタートさせている。
(Fig.40) S と S' 系におけるトルク。

Fig.39 を用いて、 S 系 (= Fig.40 左 ) と S' 系 (= Fig.40 右 ) のトルクは Fig.40 で与えられる。
もちろん、最初からゼロのため、これらのトルクは 必ず ゼロになる。
電場 E は x 方向のため、ローレンツ変換で変化しない ( E = E' )。
また 磁気モーメント μ も 両方の系で同じと見なす。
(Fig.41)

Fig.41 を用いると、 Fig.40 は、
(Fig.42) S' 系でのトルクはゼロ?

最初の項は 電気双極子 (= p ) を含み これが通常のトルクを引き起こす。
彼らは 2番目の項を 隠れた運動量だと 人為的に定義し、これが 最初の項を キャンセルするとした。
しかし この定義は Fig.40 の N = 0 の前提条件に依存している。
"ゼロ" のローレンツ変換は "ゼロ" なのは当たり前である。
つまり この方法で パラドックスを解決したことには まったくならない。
(Fig.43) 仮想の回転中心は 必要不可欠。

Fig.42 の2番目の項に含まれる速度 "v" は 仮想の半径 r = Vt から来ている。
角運動量の時間微分は トルクを与える。
彼らは Fig.43 下の 架空の関係式を トルクとして採用している。
何度も言うように、この仮想の中心は リアルなものではない。
Fig.44 では 外電場 E と 電流の磁気モーメントがある。
つまり 電磁場の運動量 ( E × H ) が存在すると言われる。
しかし これらの電磁場の運動量は いわゆる 偽の運動量である。
"本当"のエネルギーや運動量は 電線の内部やコンデンサーにある。なぜなら クーロンエネルギーは "実在"の電荷が必須だからである (もちろん 2つ以上の)。
磁気モーメントは 次のように表せる。
(Fig.44)

ここで H は 磁場の強さ、 B は 磁束密度である。
そのため 電磁場の隠れた運動量は
(Fig.45)

そのため Fig.45 を用いて、観測者の移動によって増加した角運動量を Fig.34 でキャンセルされたと彼らは 主張しているのである。
もちろん この隠れた運動量が Fig.4 の電線の回転を止めることは不可能である。
なぜなら 外電場 E は 生じた電荷そのものに作用するからである。
それに もし この -y 方向の連続した電磁場の流れ ( E×H ) がリアルだとしたら、この流れの源流はいったいどこなのだろうか?奇妙である。
また すでに述べたように、電線内部の回転トルクは その全運動量とは関係はない。

2014/5/26 updated This site is link free.