
Top page (correct Bohr model including the two-electron atoms)
Strange "spin" is NOT a real thing
Protein structure operation manual.
(Fig.1) Why quantum mechanics cannot be used in various protein interaction ?

As I said, solving multi-electron wavefunction ( Schrodinger equation ) is too difficult to be applied to computing protein interactions.
To compute macro molecules using Schrodinger equation, we have to choose "artificially" some finite basis set.
Of course, small basis set cannot get correct energy state, and various different errors happen in each different basis set.
Bond energies such as hydrogen bonds and van der Waals force, which determine actual protein interaction, are less than one-tenth of covalent bond.
For example, total ionization energies of single oxygen ( 1-6th ) is 433.11 eV, which is much bigger than covalent bond (= about 3.0 eV ) and hydrogen bond (= about 0.1 eV ).
So total errors of the whole protein due to different choice of basis set is much bigger than these small bond energies.
Density functional theory (= DFT ) is NOT "ab-initio", and it depends on rough approximation such as "LDA", which cannot deal with various protein interactions.
We need to depend on other realistic concepts such as classical Coulomb force acting on each valence electron and nuclei, giving up mathematical quantum wavefunctions.
(Fig.2) More than 80 years have passed. → QM cannot do anything.

As you know, more than 80 years have passed since quantum mechanics (QM) was born.
Even though such a long time has passed, and infinite researchers in the world tried to deal with actual protein interactions using various highly efficient computers, quantum mechanics ( and chemistry ) could NOT be used in applied fields such as medicine and industry.
These facts clearly show we cannot elucidate various complicated protein interactions ( and fatal disease ), as long as we depend on unuseful quantum mechanics. ( Because "80" years have already passed ! )
(Fig.3) "Shut up and calculate !" → we cannot advance "forever".

Of course, we understand that protein interactions are complicated, so it is very difficult to clarify their concrete mechanism.
But the most serious problem is another thing.
Though the present quantum mechanics cannot deal with complicated macro molecules, they NEVER try to elucidate the true nature of the quantum wavefunction and spin to find much easier ways.
As you notice, if we stop asking what these concepts actually are, it is impossible to make progress in these fields.
This contradictory attitude is the most serious problem in the present quantum mechanics.
(Fig.4) Molecular mechanics does NOT treat electrons.

Molecular mechanics (MM) uses classical mechanics to model molecular system.
Due to very complicated quantum wavefunctions, molecular mechanics are usually used instead of quantum chemistry in large molecules.
In MM method, bond interactions such as length and angle are treated as classical "spring".
The most important problem is MM does NOT have concepts of " electrons ".
So these classical potentials must be estimated empirically (= NOT ab-initio ).
But, for example, there are 20 kinds of amino acids, so 5 connected amino acids have as many as 20 × 20 × 20 × 20 × 20 = 3200000 kinds !
So it is impossible to determine every combination without knowing true nature of molecular bonds.
(Fig.5) Quantum mechanics = spreading electrons → total charge = zero !?

As you know, each electon is actually discrete ( NOT electron cloud ).
In fact, this realistic discrete electron's distribution is a key point in molecular bonds.
Quantum mechanics and chemistry cannot use this realistic discrete electrons, because problematic quantum wavefunction replaced Bohr's model.
But if electrons are spreading finely in every space as quantum mechanics insists, they cannot distinguish electron's orbital radius.
Because as you know, when infinitesimal electrons are distributed over some spherical shell, their potential V always becomes the same, irrelevant to radius of this sphere.
( This potential V is a function only of the distance from the center of sphere )
So, for example, the difference between fluorine and chlorine is gone, and total charges of plus and minus always become zero, because the same amounts of positive and negative charges cancel each other out.
This is very strange.
(Fig.6) H-H bond = two electrons are avoiding each other.
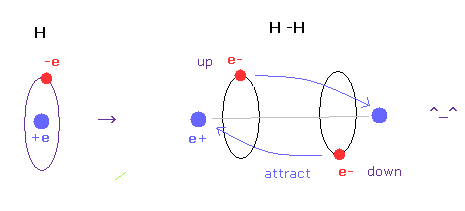
As shown in this page, we have succeeded in getting correct experimental values of hydrogen molecule and finding true meaning of H-H bond length using classical orbits in very easy and natural ways.
The key point in this calculation is that two electrons are actually avoiding each other (= up and down ).
If two electrons aren't avoiding, it is impossible to get correct bond energy of H2. ( Try it. )
Unfortunately quantum wavefunction cannot express this avoiding effects using simple model.
It must depend on very complicated determinant (= exclusion principle ) or Hylleraas functions, which cannot be applied to large molecules.
Using this program of this page, we find the protruded valence electron (= "e0" ) is the key factor to determine various covalent bond length.
(Fig.7) Comparison of forces acting on C electron.
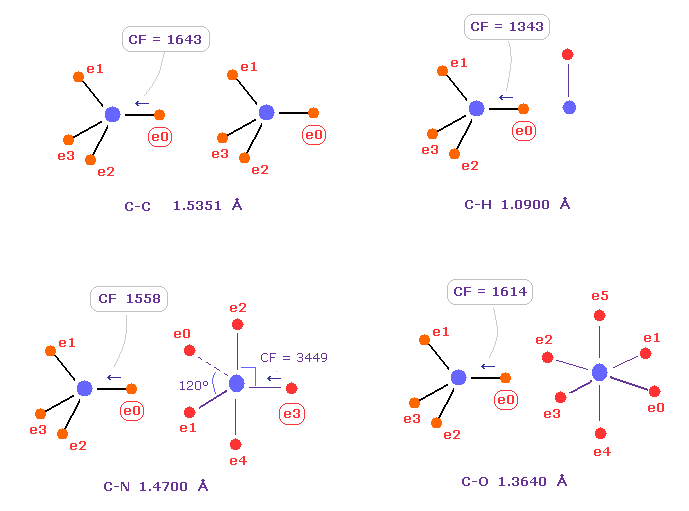
Fig.7 shows forces acting on carbon electron "e0" in C-C, C-H, C-N and C-O single bonds.
Considering carbon can keep tetrahedral structure in various bonds, it is natural forces acting on C electron are almost equal to each other.
Actually, these forces (= CF ) are 1643, 1343, 1558, 1614 in different C-C, C-H, C-N, C-O bonds, respectively.
( These bond lengths are average experimental values. C-O single bond is from acetic acid. )
| molecular bond | bond length | Force on e0 |
|---|---|---|
| C - H | 1.0900 Å | CF = 1343 |
| C - C | 1.5351 Å | CF = 1643 |
| C - N | 1.4700 Å | CF = 1558 |
| C - O | 1.3640 Å | CF = 1614 |
| C - F | 1.3500 Å | CF = 1605 |
| C - Si | 1.8500 Å | CF = 1602 |
| C - P | 1.8400 Å | CF = 1584 |
| C - S | 1.8200 Å | CF = 1708 |
| C - Cl | 1.7700 Å | CF = 1626 |
Table 1 shows forces (= CF ) acting on carbon electron "ele 0" in various bonds.
Surprisingly, in different bonds, these forces (= CF ) become almost same !
This means common mechanism is working, and carbon's tetrahedral structure is kept in various bonds.
As I said in Fig.5, the concept of "discrete" electrons is a key point, because the difference among these bond lengths are clearly caused by this property.
For example, in chlorine, its nucleus is more exposed due to 3 de Broglie wavelength, so bond length needs to be longer to make force CF the same value as other bonds.
(Fig.8) When they choose steric hindrance or covalent bonds.
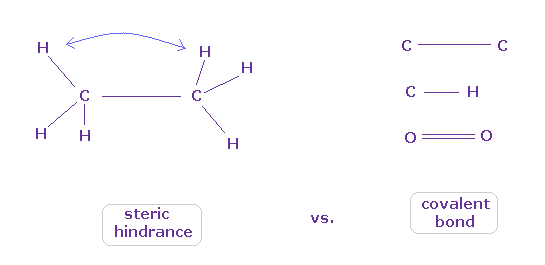
You often see the explanations such as " six hydrogen atoms of ethane tend to avoid each other." or "protein structures are very limited due to their steric hindrance".
So this means each atom "always" avoids other atoms ?
On the other hand, various atoms except for noble gases can form stable covalent bonds.
Though each atom "avoids" each other, why they can form stable and tight covalent bonds ??
(Fig.9) Lennard-Jones potential cannot explain the transition to covalent bonds
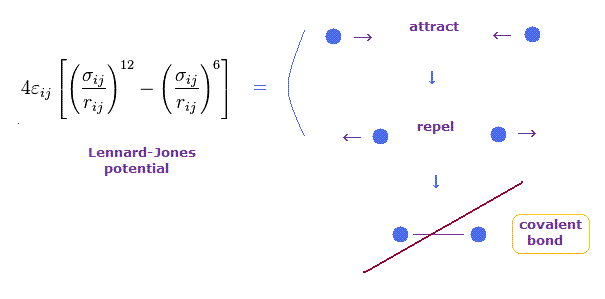
Lennard-Jones potential is often used to express forces among molecules such as van der Waals forces.
In this potential, when the distance between two particles is very long, they attract each other weakly.
On the other hand, when two particles come closer to each other than some threshold length, they start to repel each other.
This repulsive force is caused by collisions of electron cloud and Pauli exclusion principle, they insist.
But this Lennard-Jones potential cannot explain why very stable and tight covalent bonds are formed in much shorter bond length.
(Fig.10) C-C = 1.5400 Å is an equilibrium length.
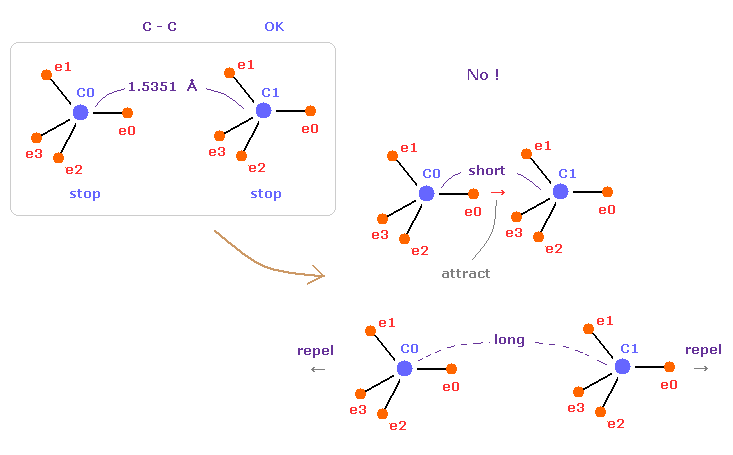
In this page, we show C-C bond length (= 1.5351 Å ) is indispensable for the stability of both C nuclei, using computer program.
If C-C bond length is shorter than 1.5351 Å, attractive force between e0 and C1 becomes too stronger, and it's unstable (= periodic electron motion is broken ).
And if C-C bond length is longer than this, repulsive force between two C nuclei becomes dominant, and it's unstable, because the influence of protruded electron "e0" is weaker.
This is the true mechanism of C-C bond length.
(Fig.11) "Long" (= middle ) or "short" bond length determines their property.
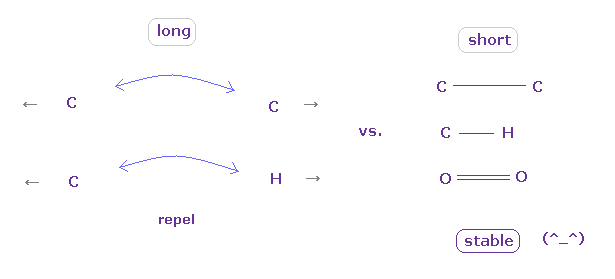
As shown in this page, to form stable covalent bonds, two atoms need to come close to each other than some threshold length.
When it is longer than the threshold length, repulsive forces among electrons or nuclei become dominant and causes steric hindrance.
As two atoms come closer to each other than some threshold length, the attractive power of protruded valence electron (= "e0" of Fig.7 ) becomes strong enough to cancel repulsive force between nuclei
And in these short covalent bond length, electrons of two atoms tend to periodically avoid each other, which is the origin of bond energy.
( These kinds of periodic avoiding motions are difficult to form in very long bond length. )
In usual proteins, almost all distances between two atoms are longer than covalent bond length, so they tend to cause steric hindrance.
(Fig.12) Glucagon structure is changing inside body.
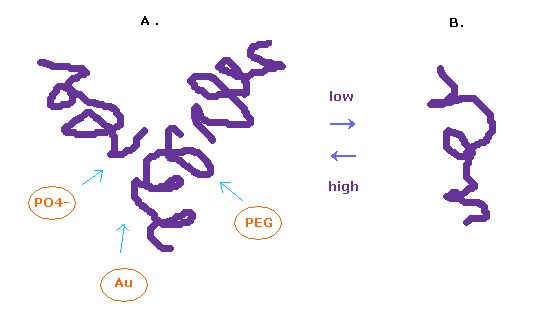
It is known that the protein structure of glucagon easily change depending on its surrounding conditions.
In the solution of high-concentration, glucagon form trimer, and in the low-concentration solution, it becomes separated.
To observe protein structure, we need to put many glucagons together and crystallize them.
We use various substances such as PEG, buffer, salt, and metals for them.
In this process, each protein get stuck in various grooves, and crystallizes.
In this page, we investigate a single isolated glucagon structure.
So these various other substances sticking to them need to be also considered for its interpretation.
(Fig.13) Glucagon 3D structure.

Glucagon is very small protein consisting of only 29 amino acids.
So it is easy to start from this simple glucagon.
Here we use the following sample JAVA program to investigate protein structure.
Sample JAVA program ( PDB protein ).
About the detailed manual, see this page first.
PDB data of glucagon ( 1GCN ) is
We save this text at the location of "C:\sdff" folder as the filename of "glucagon6.txt".
After it, save the above sample JAVA program as "protein.java", and compile it.
You can run the program, as it is, neglecting notes such as "Recompile with -Xlint: unchecked for details ".
(Fig.14) Change location folder name inside program.

When you save this text editor at some different folder, change location address at which you save this text inside the upper program. ( Change blue line of Fig.14. )
(Fig.15) Hydrogen repulsive force is very weak.

After running this program, see the potential energies (= alV ) of each atoms.
This potential energies are computed excluding fixed area near each atom, as shown in this page.
Clicking "Atom" button, you can proceed to next pages.
At first glance, you find the hydrogen's repulsive potential energies are very small comparing with other atoms such as oxygen, nitrogen, and carbon.
( In this program, positive value = repulsive V, negative value = attractive V. )
Because hydrogen nucleus is only +1 positive, and this nucleus is exposed.
(Fig.16) Valine 3D structure. Why "A" often happens ?

In Valine, conformation of A in Fig.16 is so often seen comparing with B.
Because CH3 part exerts stronger repulsive force than a single hydrogen atom, as shown in Fig.15.
So CH3 tends to avoid nitrogen and oxygen ( these repulsive force are strong, too ) .
This is the true reason why conformation of A is often seen.
Here we use this program of this page to investigate interactions between various two atoms.
(Fig.17) H -- O-H hydrogen bond.
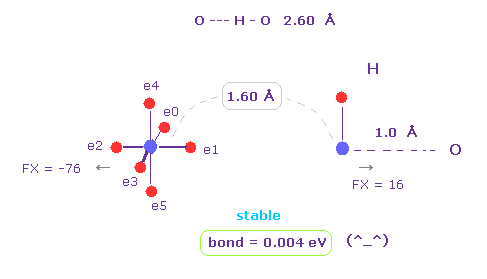
H -- O-H hydrogen bond length is about 2.60 - 2.70 Å.
We choose "O" and "H" as A and B atoms, and make internuclear distance "1.60 Å" (= 16000 MM ).
And rotate "O" atom by 45 degree on x-y plane ( input "45", and click "x-y ang" button. )
Also in this case, binding energy becomes positive (= 0.004 eV ), and O-H bond becomes stable.
And repulsive force between nuclei is FX = -76 and FX = 16.
This means O and H are slightly repelling each other, which blocks their coming closer to each other.
| O - A length | 1.90 Å | 1.80 Å | 1.70 Å | 1.60 Å | 1.50 Å | 1.40 Å | 1.30 Å |
|---|---|---|---|---|---|---|---|
| O - H | -0.011 | -0.009 | -0.004 | +0.004 | +0.022 | +0.054 | +0.113 |
| O - C | -0.205 | -0.190 | -0.158 | -0.095 | +0.020 | +0.232 | +0.612 |
| O - O | -0.261 | -0.266 | -0.265 | -0.252 | -0.215 | -0.122 | +0.092 |
At first glance, you find repulsive force by hydrogen atoms is very weak even in these short molecular length.
For example, the bond energy in the interaction O-O at 1.60 Å is negative, and its absolute value is much bigger (= -0.252 vs. +0.004 )
( In this program, when the bond energy is negative, it means they repel each other. )
This means it's very difficult for two oxygens to come close to each other to this short length.
(Fig.18) Force = 1000.
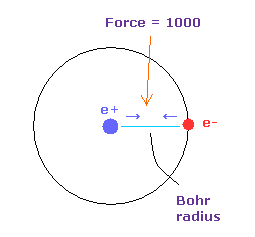
Force unit is shown in Fig.18.
The force between electron and nucleus in H atom ground state is supposed to be "1000".
So when the distance between electron and +e nucleus is Bohr radius, its force becomes 1000.
For example, the force of 1468 is 1.468 times that in H atom ground state.
| O - A length | 1.90 Å | 1.80 Å | 1.70 Å | 1.60 Å | 1.50 Å |
|---|---|---|---|---|---|
| O of ( O - H ) | 38 | 47 | 58 | 74 | 94 |
| H of ( O - H ) | 19 | 20 | 22 | 25 | 26 |
| O of ( O - O ) | 121 | 132 | 144 | 256 | 167 |
Using this program, we find repulsive force becomes stronger, when two atoms come closer to each other.
This is the reason why some molecular bond length cannot be shorter than some threshold.
( Of course, as I said, when the bond length becomes much shorter, the stable covalent bond is formed. )
As you see in Table 3, repulsive force in O-O interaction is much bigger than O-H bond.
( These repulsive force is the average value, when oxygen's electron is rotated 45 degree on x-y plane and not. )
Actually, O-O molecular bond of this short length is not seen in various proteins.
Probably the forces between 1.70 Å and 1.60 Å in O-H are the upper limit of repulsive force.
(Fig.19) Command prompt.

After running this program, the values of Fig.19 is displayed on the command prompt screen.
For example "H:13-H:24= 1.2918" means the distance between hydrogen atoms of "13" and "24" (= absolute atomic number, see this page )
is 1.2918 Å.
As I said in the upper section, due to stronger repulsive forces, there are some lowest limit of interatomic distance (= not covalent ).
These values show interatomic length near these lowest distance inside the whole glucagon .
( H-H= 1.3 Å, O-O, N-O, C-O = 2.6 Å, C-C, C-N, N-N = 2.5 Å, O-H, N-H, C-H = 1.7 Å. )
(Fig.20) O-O length = 2.557 Å

As shown in Fig.19, the lower limit of O-O interatomic length in glucagon is 2.5577 Å.
When O-O interatomic length is this value, average repulsive foerce is about 70.
Actually, repulsive force between oxygen 56 and 58 is about 70, also in this program.
( Detailed method, see this page. )
| O - O length | 5.0 Å | 4.5 Å | 4.0 Å | 3.5 Å | 3.0 Å | 2.5 Å | 2.0 Å |
|---|---|---|---|---|---|---|---|
| O1 of ( O - O ) | 19 | 23 | 30 | 39 | 53 | 78 | 125 |
| O2 of ( O - O ) | 19 | 23 | 29 | 38 | 51 | 71 | 97 |
| Average force | 19 | 23 | 29.5 | 38.5 | 52 | 75 | 111 |
Table 4 is the result, which shows repulsive force between oxygens in various molecular bond length using this program.
As you see, the change of forces become bigger in less than 2.6 Å length.
Probably, this is the reason why O-O interatomic distance cannot be shorter than some value due to the steric hindrance.
(Fig.21) N-O length = 2.600 Å

The lower limit of N-O interatomic length in glucagon is about 2.600 Å, too.
When N-O interatomic distance is this value, average repulsive foerce is 57 in N, and 70 in O.
So also in this case, maximam repulsive force in molecular interaction is about 70.
(Fig.22) H-H length = 1.290 Å

The lower limit of H-H interatomic length in glucagon is about 1.290 Å.
When H-H interatomic distance is this value, average repulsive foerce is 26.
Hydrogen has only one electrons, so it has no ability to cope with stronger repulsive force like oxygen or nitrogen.
The important point is that in H-H case, bond energy becomes positive (= 0.381 eV ), which means stable bond.
But of course, for getting this stable bond energy, two electrons of H-H need to be periodically avoiding each other (= up and down ).
Basically hydrogen atom binds to other atoms such as carbon and nitrogen, and harmonize with them.
So it cannot afford to harmonize also with another hydrogen.
(Fig.23) Hydrogen's orbit can lean ?

Basically, when the distance between two hydrogen atoms is very short, the conformation of Fig.23 is impossible.
Because, in Fig.23, valence electron at position "a" is attracted toward another hydrogen nucleus too much to return to position "b".
In Fig,23 case, attractive force and bond energy become unrealistically too strong.
H-H distance is usually much shorter than other interatomic distances, so we need to be very careful about its interpretation.
(Fig.24) Average hydrogen electron's distribution.

And in this program, we use Fig.24 average hydrogen electron's distribution, in which we use four -0.25e electron instead of one -e electron.
As two atoms come very close to each other, we need to consider "avoiding" effect like Fig.22.
But this program doesn't consider this effect.
So we need to think about this very short length, combining the concept of forces in addition to potential energy.
(Fig.25) Force change after chain rotation at C (= "2" ).

As shown in this page,
we rotate amino acid chain at 2-C-HIS (= histidine, carbon atom "2" ) by 10 degree, and investigate how potential energies change.
We want to rotate all amino acids after this 2-C atoms, so input "500" (= more than maximam atom ) into "to=" textbox, and input "2" into "from (dire)=" textbox, then click "chain rot" button.
After chain rotation, computing all interactions takes a little time.
After this rotation, dihedral angle at 2-C changes from -159.3 into -149.3 degree. ( Try confirming it. )
When you click " =back " button, it returns to the original protein state (= not rotated state ).
(Fig.26) Command prompt

After chain rotation, one part of results are displayed on the command prompt screen.
Basically non-covalent bond has some minimum distance allowed between atoms due to stronger repulsive force, as I said in Fig.19.
In Fig.26 first line, the distance between HIS-CB-4 (= histidine side chain, carbon ) and SER-N-18 (= serine main chain, nitrogen ) becomes too short ( from 2.5407 Å to 2.4867 Å ).
This interatomic length is too short considering steric hindrance.
"Energy change = 0.5470 (eV)" means total potential energy becomes bigger by this chain rotation.
( This value is potential energy itself, so positive = repulsive, negative = attractive. )
So this rotation doesn't happen so easily and the original protein conformation is stable.
(Fig.27) Potential change in 18-N-SER.

"Plus" line of Fig.26 picks up atoms which potential energies become much bigger.
Input "18" (= absolute atomic numebr ) and click "select" button.
And click "V change", and then"FX rela" button.
As shown in Fig.27, the change of potential energies (= c,aV ) of 18-N-SER is +0.1271 eV
In "dis (A)" column of 15, 16, 17-H4-HIS, the distance between 18-N-SER (= serine main chain, nitrogen ) and histidine side chain ( hydrogen ) becomes shorter.
( For example, "cha-0.1867" means the distance between 18-N-SER and 15-H4-HIS becomes shorter by 0.1867 Å )
(Fig.28) Reason why potential change of 18-N-SER becomes higher.
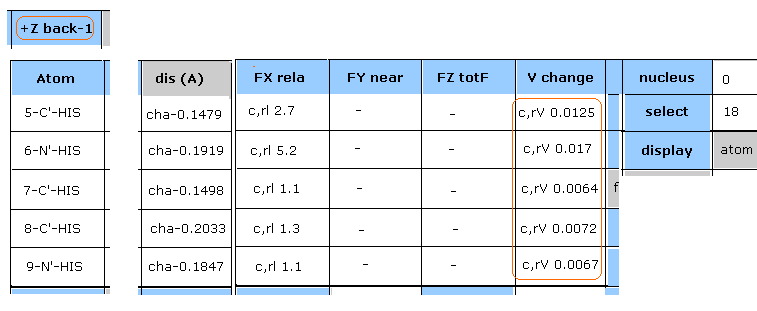
Hydrogen energy change is negligible, as shown in Fig.27.
Then, click "+Z back-1" button twice, returning to two pages back.
In Fig.28, the potential energies of all atoms included in histidine become higher, because they are closer to 18-N-SER by this chain rotation.
(Fig.29) Histidine → 18-nitrogen.
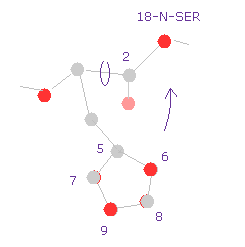
So the shorter distance between histidine side chain and serine atom is the main reason why the total potential energy becomes higher by this rotation.
Caution: potential energy change of Fig.26 sees only atomic interactions within 5.0 Å near area from each atom.
So when the numbers of atoms inside this area increase, this potential energy change is not equal to the sum of each potential energy change.
( Each potential energy change also includes the cases in which the distance changes from 6.0 Å to 4.9 Å. So even when only the last distance is within 5.0 Å, this energy change is computed. )
(Fig.30) Histidine → glutamine.

Next we click " =back " button, and return to the original conformation.
Then input "-10" into the textbox next to "angle=" button, and click "chain rot" button.
As shown in command prompt, also -10 rotation at 2-C, the total potential energy becomes higher (= +1.1613 ).
For example, if you select "8" carbon of histidine side chain, you find the shorter distances between histidine and glutamine (= GLN ) is the main reason of this energy increase.
This means the side chain of histidine is sandwiched between serine and glutamine.
(Fig.31) 20-C-SER rotation (+10)

Next we rotate 10 degree at 20-C-SER.
Click "=back", input "20" into "from (dire)=" textbox, input "10" into "angle=", and then click "chain rot" button.
Also in this case, total poential energy becomes higher (= +0.4650 eV ), because the histidine side chain come closer to glutamine.
( So, the potential energies of "5","6","8" (= HIS ) and "33", "34", "35", "36" (= GLN ) atoms increase. )
(Fig.32) 20-C-SER rotation ( -10, -20 )

Next we rotate -10 degree at 20-C-SER.
Click "=back", input "-10" into "angle=", and then click "chain rot" button.
In this case, total poential energy becomes lower, because the histidine side chain get away from glutamine.
( So, the potential energies of "8","9" (= HIS ) and "33", "34", "36" (= GLN ) atoms become lower, as shown in "Minus" line. )
Click "chain rot" button, again, which means total rotation angle is -20 degree.
In this case, the total potential energy becomes higher (= +0.1650 eV ), because histidine come cloer to glycine atoms.
( So there is some room in this rotation. )
(Fig.33) "Gaps" are filled with other proteins or salts.

The problem is that variable parts near glycine are fixed by other protein projection or salts in protein crystals.
Because putting many proteins together is indispensable for protein crystal analysis.
So, for example, if you rotate at 47-CA-GLY, wide rotation angles are allowed, and cannot detemine one conformation, which indicates there are some other things stuck into this hollow.
Almost all parts are stable in this conformation.
But glucagon is very small protein, so there are some parts where we need to consider other surrounding proteins stuck to each other.
(Fig.34) Different bond lengths are caused by "discrete" electrons.

Anyway, considering correct electron's distribution is indispensable for understaning of actual protein structures and actions.
As shown in this page, difference between O-F ( or C-F, fluorine ) and O-Cl ( or C-Cl, chlorine ) bond lengths are caused by discrete electrons.
If all electrons are spreading smoothly around the nucleus, their difference is gone, as I explain in Fig.5.
Of course, to use these discrete electrons inside proteins, we have to give up very vague concept of quantum wavefunction.
---------------------------
If you have some molecular models, you can easily understand these conformation change.
And you can easily construct those models, using this program ( x-y, x-z, y-z planes ).

2013/7/9 updated. Feel free to link to this site.