Top page (correct Bohr model including the two-electron atoms).
Electron spin is an illusion !
Bohr's single and double bonds
Our new Bohr model has succeeded in calculating the Helium ionization energy more correctly than the quantum mechanical variational methods as shown in the Top page.
In this new successful Bohr model, the two electrons of the helium atom (He) are moving on the orbits of just one de Broglie's wavelength, which are perpendicular to each other.
Furthermore, we have succeeded in visualizing the four valence electrons of carbon , and six valence electrons of oxygen.
(See Carbon page and Oxygen page).
In this page, we calculate the orbits of hydrogen molecule (H2) concretely.
Here we try to prove that the two electrons of hydrogen molecule (H2) are moving on just 1 de Broglie's wavelength orbits using the Virial theorem.
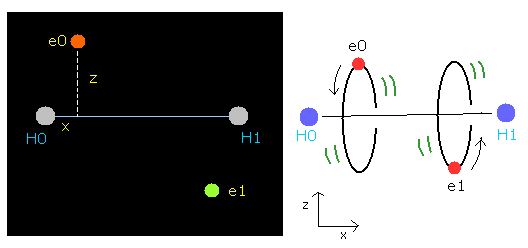
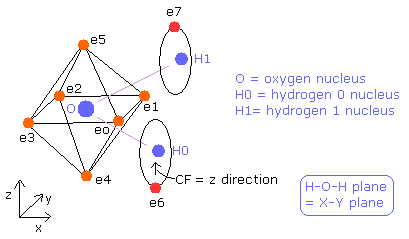
The hydrogen molecule ( H2 ) has two protons ( H0, H1 ) and two electrons ( e0, e1 ).
The bond (binding or dissociation ) energy is 4.7467 eV.
So the ground state energy of H2 becomes - 27.212 ( H × 2 ) - 4.7467 = - 31.9587 eV.
And the equilibrium internuclear distance (or bond length) ( = nleng ) is about 0.7414 × 10-10 m. ( = 7414 MM), which is a little longer than the Bohr radius (5292 MM ).
(Here, we use the new convenient unit, 1 MM = 10-14 meter.)
Fig. 1. Hydrogen molecule ( H2 )

According to the Virial theorem, the two-atom molecule of the equilibrium state (equilibrium internuclear distance) satisfies the next relation.
2 < T > + < V > = 0
E = < T > + < V >
where T is the "average" kinetic energy, and V is the "average" potential energy.
The ground state energy (= E) of H2 is -31.9587 eV.
So, in the state of equilibrium, the potential energy is -31.9587 eV × 2 = - 63.9174 eV.
Here we use the next sample JAVA program to show the orbital length becomes just 1 de Broglie's wavelength in this condition.
Sample JAVA program of H2 (Virial theorem).
This program is a little long. So if you copy and paste the program source code into a text editor,
you can easily compile and run this.
This program's class file name is hydd, so save this text editor as "hydd.java", and compile it.
In this program, the hydrogen nuclei are gray circles.
Each coordinate of electrons (+X (MM), +Z (MM)) in the text box means "relative" position from these nuclei.
(ele 0 is from hydrogen nucleus 0 (H0), and ele 1 is from H1.)
(FX, FZ) means the force component acting on each particle (electrons or nuclei).
(Unit of the force: 1000 = force between +e nucleus and -e electron which are Bohr radius apart.)
tV (eV) means the total potential energy.
Waves (wn) is number of de Broglie's waves contained in one orbit.
You can change the coordinates (+X, +Z) of electrons and the internuclear distance freely.
(Enter the values into the textbox, and press the Enter key.)
Based on each kinetic energy (T), we calculate each electron's velocity ( = v (m/s) ).
Using this velocity (v) and the force acting on each electron (F), we suppose the centrifugal force is equal to this force (F), as follows,
(Eq.1)
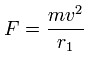
This r1 is "temporary" radius, which appears by this relation.
Using this r1, we can calculate the number of de Broglie's waves (wn) contained in one orbit, as follows,
(Eq.2)
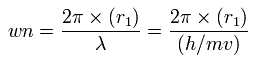
Surprisingly, when the electrons' positions are stable (FX = 0), de broglie's waves (wn) becomes just 1.0 as shown in Table 1 and 2.
| tV (eV) | X (MM) | Z (MM) | FX | FZ | nleng | Waves(wn) |
|---|---|---|---|---|---|---|
| -60.0 | 1154 | 4984 | 0 | -1077 | 7414 | 1.037 |
| -62.0 | 996 | 4816 | 0 | -1154 | 7414 | 1.017 |
| -63.91 | 890 | 4665 | 0 | -1227 | 7414 | 1.001 |
| -65.0 | 830 | 4583 | 0 | -1271 | 7414 | 0.991 |
| -67.0 | 740 | 4440 | 0 | -1352 | 7414 | 0.975 |
The experimental value of the internuclear distance (= nleng) is 7414 MM.
And when the total potential energy (tV) is -63.91 eV (= experimental value), the number of de Broglie's waves (wn) becomes just 1.001.
Table 2 changes this distance as follows,
| nleng (MM) | X (MM) | Z (MM) | FX | FX (nuc) | eleng (MM) | tV (eV) |
|---|---|---|---|---|---|---|
| 6500 | 1275 | 4630 | 0 | 86 | 3950 | -64.76 |
| 7000 | 1025 | 4645 | 0 | 78 | 4950 | -64.34 |
| 7414 | 890 | 4665 | 0 | 74 | 5634 | -63.91 |
| 8000 | 730 | 4677 | 0 | 67 | 6540 | -63.53 |
| 8500 | 628 | 4710 | 0 | 59 | 7244 | -62.94 |
As shown in Table 2, when the internuclear distance (=nleng) is 7414 MM, total potential energy (tV) becomes -63.91 eV (= experimental value).
So this means that we can use the idea of Eq.1 and Eq.2 with the Virial theorem in H2 molecule.
In Table 2, as the internuclear distance becomes longer, the total potential energy (tV) becomes higher, which means H-H bond becomes more unstable.
On the other hand, as the internuclear distance becomes shorter, the force (FX(nuc)) acting on the H0 nucleus becomes stronger, which means the nuclear positions become unstable.
And when the nleng is 7414 MM (experimental value), the distance (eleng) between x positions of the two electrons is 5634 MM ( = 7414 - 2 × 890).
When the nleng is shorter than 7414 MM, this eleng becomes shorter than Bohr radius (= 5292 MM).
So probably, "7414 MM" is the proper value in which both the electrons and nuclei are stable.
(Caution: the hydrogen atom has only one electron, so it is almost impossible that we make the nuclear positions stable (= FX (nuc) and FZ (nuc) are zero.) only in one scene, which is different from other atoms such as carbon and oxygen.)
As shown in this oxygen page, we have succeeded in visualizing the six valence electrons' motion using this JAVA program.
When the total energy is supposed to be the sum of 1-6th ionization energies (= -433.103 eV), all six electrons can be back after moving their 1.9 (almost 2.0) de Broglie's wavelength orbits.
But actually, the two 1S electrons are a little apart from the +8e oxygen nucleus, so the "effective" positive central charge, which influence these valence electrons is a little bigger than +6e (= +8e -2e).
When this central charge is +6.3e instead of +6e, all six electrons can be back after moving just 2 de Broglie's wavelength orbits.
Fig. 2. Oxygen electrons at wn = 0.0 and wn = 2.0 ("effective" charge = +6.3e)
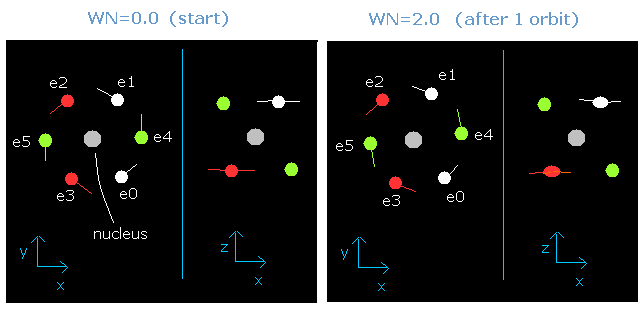
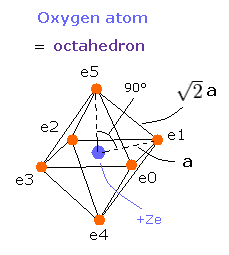
Furthermore, this motion is linked to the Virial theorem combined with "octahedron" model.
Fig. 3. Oxygen valence electrons ("effective" charge = +Ze)
About the detailed calculation method, see this page.
According to the Virial theorem, total potential energy (tV) of six valence electrons is 2 × -433.103 = -866.206 eV
(The kinetic energy (T) is 433.103 eV.)
Based on these tV and T values, we can know the length a of Fig.3 and electron's velocity.
If we know the a of Fig. 3, we can determine the force (F) acting on each electron.
We suppose the centrifugal force is equal to this force (F), as follows,
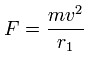
This r1 is "temporary" radius, which appears by this relation.
Using this r1, we can calculate the number of de Broglie's waves (wn) contained in one orbit, as follows,
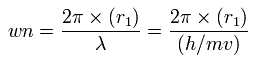
When Z = 6.0, this wn becomes 1.88 (almost 1.9).
And when Z = 6.3, this wn becomes just 2.01.
Also in the carbon atom, the "tetrahedral" model can be used with Virial theorem. (See this page.)
In the upper section, we succeeded in calculating de Broglie's waves of H2 using the force (F) acting on each hydrogen (H) electron.
In the hydrogen molecule (H2), the direction of this force (F) is perpendicular to the H-H bonding line.
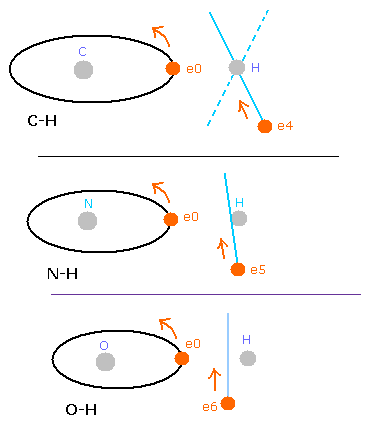
But in the oxygen or carbon atoms, the forces of some eletrons (for example, e0, and e1 of Fig.4A) are parallel to the bonding line.
Fig. 4. Force directions of O-H bond
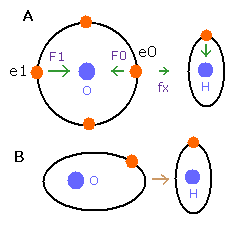
In the e0 and e1 of Fig.4A, we can not use the upper calculating method of de Broglie's waves.
In the electron 0 (e0) of oxygen (O), due to the opposite attractive force (fx) from the hydrogen nucleus, force F0 becomes weaker than force F1 of electron 1, as shown in Fig.4A.
So, in Eq.1, "temporary" radius r1 of e0 becomes longer than e1.
This means more de Broglie's waves (> 2.0) are contained in e0 orbit than e1 (< 2.0), when we use the calculating methods of Eq.1 and Eq.2.
But if we pay attention to only one electron's orbit (Fig. 4B), the number of de Broglie's waves ( = 2.0) is kept by changing the position and shape of its orbit.
(A positive H nucleus translates this electron's orbit a little, and make it "elliptical".)
So we have to calculate the "average" de Broglie's waves of all orbits in oxygen atom.
Fig. 5. Change of "octahedral" structure in O-H bond
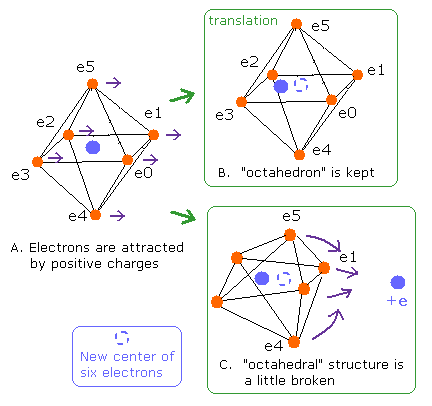
If all valence electrons of oxygen are attracted by the same force, all orbits are translated equally, and "octahedral" structure is kept. (Fig. 5B).
In this case of Fig.5B, all numbers of de Broglie's waves need to be 2.0.
But if these valence electrons are attracted unequally by other positive nuclei, "octahedral" structure becomes broken (Fig. 5C).
How can we distinguish these changes (Fig. 5B and 5C) ?
If we use the new center of six valence electrons as a nucleus, all de Broglie's waves of Fig. 5B are kept to be 2.0 like Fig.5A.
But in Fig. 5C, it is possible that some de Broglie's waves are different from 2.0 due to the change of octahedron, even if we use the new center of six electrons.
So we use this new centers of valence electrons of oxygen ,carbon and nitrogen in the chemical bond's program below.
(coordinates of the new center = noxx[0-2], force component of each electron based on this new center = teqq[el][0-2])
Acoording to the Virial theorem, the average potential energy (V) and kinetic energy (T) satisfy the relation, -1/2 V = T.
In the case of atoms, it is easy to calculate each electron's V, because there is only one nucleus.
But in the case of molecules, it is a little complicated, because V needs to include the repulsive potential energy between nuclei.
The problem is how this repulsive potential energy between nuclei should be distributed to each electron.
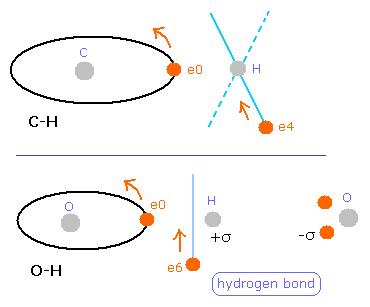
For example, in the O-H bond of water, two positive nuclei needs to be attracted by electrons which belong to another nucleus. (Fig. 6)
Fig. 6. O-H bond and the change of each potential energy
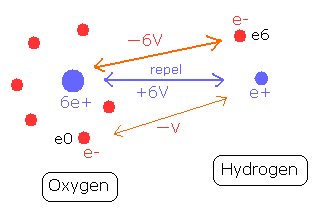
The hydrogen nucleus (e+) is attracted by the six electrons of the oxygen atom.
The potential energy between the hydrogen nucleus and one electron (e0) of oxygen is -V.
On the other hand, the oxygen nucleus is attracted only by one electron (e6) of hydrogen atom, so the potential energy between the oxygen nucleus and the hydrogen electron (e6) is - 6V, which bond is six times stronger than the above case.
So the potential energy of the hydrogen electron (e6) becomes -6V lower by O-H bond, but instead, e6 does much work to bind two repulsive positive nuclei, which makes the e6 potential energy higher than this.
Considering this fact, in the programs below, after calculating potential energies between electron-electoron and electron-nucleus, the potential energies between repulsive positive nuclei are distributed to each electron.
For example, when this repulsive potential energy is +6V, the distribution ratio is 6:1 in e6 and e0. (= -6V: -V )
As the oxygen has six e0-e5 electrons, +6V × 6/(1x6 +6) = +6V / 2 is distributed to e6, and +6V × 1/(1x6+6)= +6V / 12 is distributed to e0.
(In the programs below, we calculate each electron's interaction ( = rhp[el][5] ) with other nuclei, And in proportion to this rhp[el][5], the repulsive potential energy between nuclei are distributed to each electron.)
And then, based on each electron's potential energy, the kinetic energy is distributed to each electron.
Basically, the two particles at the both ends of "attractive" or "repulsive" force (Fa) receive the same force (Fa).
In the hydrogen atom side, only one electron (e6) receives this force.
On the other hand, in the oxygen side, this force is divided into six electrons.
So the above principle is effective.
Breaking all four C-H bonds of methane requires 1663 kJ/mol ( = 17.235 eV ).
So the ground state energy of methane (4 carbon's valence electrons + 4 hydrogen atoms) becomes -148.024 -54.416 -17.235 = 219.675 eV.
(Here, the total energy of the four valence electrons of carbon is supposed to be -148.024 eV = sum of 1-4 ionization energies.)
And the average bond length of C-H bond is 1.09 × 10-10 meter (=10900 MM).
Fig. 7. Carbon valence electrons ("effective" charge = +Ze)
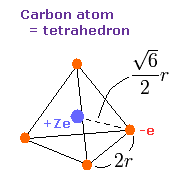
As shown in carbon page, the motions of carbon's valence electrons can be linked to the "tetrahedral" structure with Virial theorem.
According to the Virial theorem, the "average" potential energy (V) becomes 2 × -148.024 (E) = -296.048 eV.
(The total kinetic energy (T) = 148.024 eV.)
Based on this value (V), the length (2r) of Fig.7 is determined.
(r becomes 5260 MM in this condition.)
If the value 2r is determined, we can know the force (F) acting on each electron.
We suppose the centrifugal force is equal to this force (F), as follows,
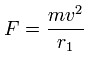
This r1 is "temporary" radius, which appears by this relation.
Using this r1, we can calculate the number of de Broglie's waves (wn) contained in one orbit, as follows,
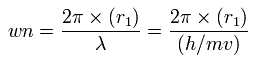
When Z = +4.0, this wn becomes 1.87 (almost 1.9).
And when Z = +4.25, this wn becomes just 2.02.
(In this section., we use Z=+4.23. So wn becomes 2.007 (almost 2.0).)
In this section, we utilize this simple tetrahedral structure for calculating the C-H bond of methane (CH4).
Fig. 8. Estimated metahne (CH4) model
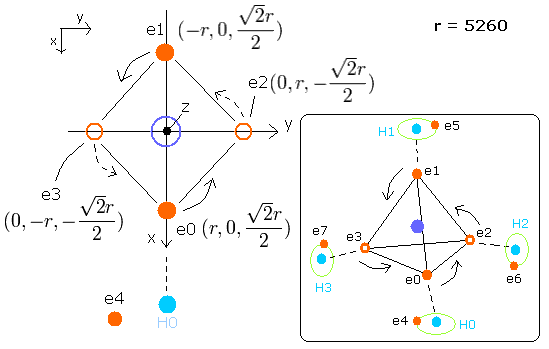
Sample JAVA program of CH4 (Virial theorem)
In this program, nuclei are gray circles.
Each particle of CH4 is shown on the X-Y (left), X-Z (center), and Y-Z (right) planes.
You can change the coordinate (+X, +Y, +Z) of only electron 4 (ele4), because four hydrogen atoms and four carbons's valence electrons are always symmetrically arranged in CH4.
(Enter the values into the textbox of ele4, and press the Enter key.)
CF of ele0-3 means the force toward the center, CF of ele4-7 means the force toward each C-H line. (= perpendicular to C-H line).
(fx, fy, fz) means force components other than CF.
(Here, as the direction of this central force CF in ele0-3, we use the array variables rpp[el][0-2].
rpp[el][0-2] means the total force components of carbon nucleus, four hydrogen's nuclei and four 4-7 electrons. )
Fig. 9. C-H bond of methane (Virial theorem)
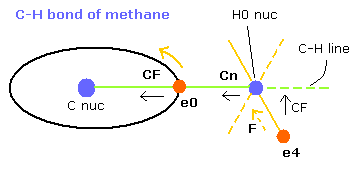
(FX, FY, FZ) means the force component acting on each nucleus.
Cn means the force component acting on each H nucleus toward the C nucleus.
Waves (wn) is number of de Broglie's waves contained in one orbit.
when you choose the C-H bond length (MM) in the scrollbar and click "C-H (MM)" button, the internuclear distance of C-H change.
According to the Virial theorem, total potential energy (tV) of CH4 is - 219.675 × 2 = -439.3 eV.
When tV is -439.3 eV and de Broglie's waves are 2.0 (carbon) and 1.0 (hydrogen), how are eight electrons of methane distributed ?
When the electron 0 (e0) is at the position of Fig.9, it is the closest to H0 nucleus.
(When the C-H length is 10900, the distance between e0 and H0 nucleus is about 4500 MM )
So in this state, e4 is at the opposite position of H0 nucleus from e0, and Cn needs to be as small as possible to make the H0 nucleus stable.
Fig. 10. CH4 distribution (C-H = 10900 MM, tV= -440.53 eV)
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 5260 | 0 | 3719 | 6442 | 1249 | -1 | 0 | 1 | 2.007 |
| ele 1 | -5260 | 0 | 3719 | 6442 | 1249 | 1 | 0 | 1 | 2.007 |
| ele 2 | 0 | 5260 | -3719 | 6442 | 1249 | 0 | -1 | -1 | 2.007 |
| ele 3 | 0 | -5260 | -3719 | 6442 | 1249 | 0 | 1 | -1 | 2.007 |
| ele 4 | 1850 | -4152 | 1820 | 4896 | 858 | -481 | 0 | -340 | 0.999 |
| ele 5 | -1850 | 4152 | 1820 | 4896 | 858 | 481 | 0 | -340 | 0.999 |
| ele 6 | 4152 | 1850 | -1819 | 4896 | 858 | 0 | -481 | 340 | 0.999 |
| ele 7 | -4152 | -1850 | -1819 | 4896 | 858 | 0 | 481 | 340 | 0.999 |
Table 3 shows that we can combine de Broglie's wave conditions with experimental value properly.
(In Table 3. tV is -440.53 eV (experimental value -439.3 eV), and de Broglie's waves are 2.007 (almost 2.0) and 0.999 (almost 1.0) in carbon and hydrogen.)
According to this result, electrons of hydrogen nuclei are thought to be moving and precessing like e4 of Fig.9.
The electron 4 is attracted in the direction of hydrogen nucleus, so force (F) is different from CF (= toward C-H line).
When the C-H length is 10900 MM, the smallest value of Cn (Fig.9) is 101.
(Unit of the force: 1000 = force between +e nucleus and -e electron which are Bohr radius apart.)
If you try to decrease this value 101 of Cn keeping de Broglie's waves 0.999 of ele 4, you will know that 101 is the smallest value of Cn.
At this Cn (=101), tV beceomes -440.53 eV, which is almost same as the experimental value.
In Fig.9, the electron 0 (e0) is the closest to H0 nucleus, so Cn of H0 nucleus is thought to be a little bigger than zero.
Next we choose the "9500", "10000", or "11400" in the scrollbar, and click "C-H (MM)" button.
Automatically, eight electrons of methane are distributed to satisfy the next two conditions.
1. de Broglie's waves: (C = 2.007, H = 0.999).
2. Cn is as small as possible at each nuclear distance.
| C-H (MM) | X (ele4) | Y (ele4) | Z (ele4) | CF (ele0) | Cn (H0) | Wave (ele0) | Wave (ele4) | tV (eV) |
|---|---|---|---|---|---|---|---|---|
| 9500 | 1700 | -2940 | 2070 | -24 | 846 | 2.007 | 0.999 | -498.5 |
| 10000 | 1400 | -3289 | 2500 | 609 | 467 | 2.007 | 0.999 | -471.1 |
| 10900 | 1850 | -4152 | 1820 | 1249 | 101 | 2.007 | 0.999 | -440.5 |
| 11400 | 1600 | -4379 | 2000 | 1462 | -7 | 2.007 | 0.999 | -430.6 |
Table 4 shows that when C-H bond length is 10900 MM (experimental value), tV becomes -440.5 eV (almost experimental value).
When C-H bond length is shorter than 10900 MM, the hydrogen nucleus (H0) becomes unstable.
When the C-H bond length is 10000 MM, H0 nucleus is closer to electron 0, so Cn (force acting on H0 nucleus toward C nucleus) becomes "unnaturally" bigger (Cn = 467). (See also Fig. 9)
(Unit of the force, 1000 = force between +e nucleus and -e electron which are Bohr radius apart from each other.)
In this case, force acting on electron 0 toward C nucleus (CF) is almost same as Cn (CF = 609, Cn=467).
It is ridiculous !
When C-H bond length is 9500 MM, H0 nucleus is much closer to electron 0, so electron 0 is attracted by H0 nucleus instead of C nucleus ! (CF(ele0) = -24, Cn(H0) =846) (See also Fig. 9).
If you run this program, and try changing the electron's coordinate freely, you will know this Cn can not be decreased when de Broglie's wave condition is satisfied.
When C-H bond length is 10900 MM, Cn (H0) is small enough to be stable (Cn(H0)=101), and CF (ele0) is big enough to be attracted by C nucleus. (CF(ele0) = 1249)
When C-H bond length is longer (11400 MM), tV becomes higher than the experimental value ( tV = -430.6 eV > - 439.3 eV).
So the bond state becomes more unstable than 10900 MM.
(The hydrogen atom has only one electron, so it is thought to be natural that Cn is not zero only in one scene.
But it is unnatural that Cn becomes more than 400-500. )
Next we try H2O molecular structure using the Virial theorem.
The average single O-H bond energy of the water is 9.6066 eV (=926.9 kJ/mol) / 2 = 4.8033 eV.
So the total energy of H2O is -433.103 (O) - 2 × 13.606 (H) - 9.6066 (bond energy) = -469.92 eV.
The O-H bond length of H2O is 9584 MM (= 0.9584 × 10-10 meter).
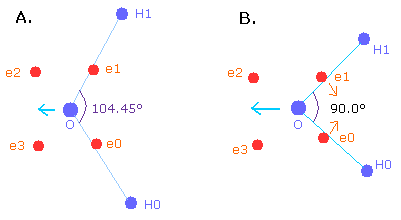
The H-O-H angle is 104.45 degrees, which is a little larger than 90 degrees (e0 - nucleus - e1 angle of oxygen).
Fig. 11. Estimated Water (H2O) model.
Using the next program, we seek for the structure of water (H2O) molecule.
Sample JAVA program of H2O (Virial theorem)
In this program, we suppose the "central" charge is +6.273 (de Broglie's wave becomes 2.00 in Fig.3) instead of +6.3 (waves becomes 2.01 in Fig.3).
This program is a little long. So if you copy and paste the program source code into a text editor,
you can easily compile and run this.
This program's class file name is watr, so save this text editor as "watr.java", and compile it.
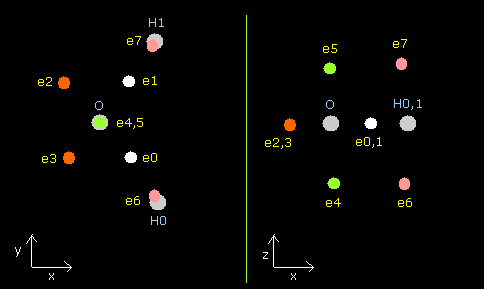
In this program, nuclei are gray circles.
Each particle of H2O is shown on the X-Y (left), X-Z (center), and Y-Z (right) planes.
Each coordinate of electrons (+X (MM), +Y (MM), +Z (MM)) in the text box means "relative" position from these nuclei.
(ele 0-5 are from oxygen nucleus, ele 6 is from hydrogen nucleus 0 (H0), and ele7 is from H1.)
You can change the coordinate (+X, +Y, +Z) freely.
CF of ele0-5 means the force toward the center, CF of ele6,7 means the force toward H-O-H plane (= + z direction).
(fx, fy, fz) mean force components other than CF.
H0, On mean the force toward H0 nucleus and O nucleus.
when you choose the O-H bond length (MM) in the scrollbar and click "O-H (MM)" button, the internuclear distance of O-H change.
And when you choose the angle in the scrollbar and click "angle" button, H-O-H angle changes.
Six valence electrons of oxygen atom are equally distributed around the nucleus.
In oxygen atom, if we suppose the CF is the force toward the nucleus, (fx, fy, fz), which are force components other than CF, become zero, when the six electrons are distributed "octahedrally".
But in water molecule, we need to consider two hydrogen atoms in addition to oxygen atom.
So the CF in H2O includes the two hydrogen nuclei and electrons in addition to the oxygen nucleus.
(In the program, array variables rpp[el][0-2] mean the force components toward CF, which is the total force from oxygen nucleus, two hydrogen's nuclei and hydrogen's electrons.)
Fig. 12. Structure of water (H2O) molecule.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 3151 | -3244 | 0 | 4522 | 5586 | 1 | 1 | 0 | 1.989 |
| ele 1 | 3151 | 3244 | 0 | 4522 | 5586 | 1 | -1 | 0 | 1.989 |
| ele 2 | -3290 | 3290 | 0 | 4652 | 5723 | 0 | 0 | 0 | 2.011 |
| ele 3 | -3290 | -3290 | 0 | 4652 | 5723 | 0 | 0 | 0 | 2.011 |
| ele 4 | 0 | 0 | -4557 | 4557 | 6110 | 0 | 0 | 0 | 1.989 |
| ele 5 | 0 | 0 | 4556 | 4556 | 6113 | 0 | 0 | 0 | 1.989 |
| ele 6 | -260 | 319 | -4535 | 4553 | 1232 | 7 | -4 | 0 | 0.995 |
| ele 7 | -260 | -319 | 4535 | 4553 | -1232 | 7 | 3 | 0 | 0.995 |
In the equilibrium state, (fx, fy, fz) need to be as small as possible. (less than 10, if possible.)
In H2O, electrons 6 and 7 are a little closer to oxygen than CH4, so (fx, fy, fz) of ele6,7 are almost zero.
(Unit of the force: 1000 = force between +e nucleus and -e electron which are Bohr radius apart from each other.)
In Table 5, the total potential energy (tV) becomes -938.18 eV, which is almost same as the experimental value (-469.92 × 2 = -939.84 eV)
When we try to make the oxygen nucleus stable (FX = -9, FY = 0, FZ= 3 of O nuc), "octahedral" structure are a little broken.
So de Broglie's waves of electrons 0-5 are a little different from 2.00 in Table 5.
(The error is ± 0.011.)
By the way, why is the angle (H-O-H) 104.45 degrees (not 90 degrees) ?
Next we choose the angle "90.0" in the scrollbar, and click "angle" button.
Automatically, the proper condition (= (fx, fy, fz) of ele and (FX, FY, FZ) of O nuc are small) is chosen.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 3214 | -3215 | 0 | 4545 | 5480 | 2 | 2 | 0 | 1.99 |
| ele 1 | 3214 | 3215 | 0 | 4545 | 5480 | 2 | -2 | 0 | 1.99 |
| ele 2 | -3284 | 3293 | -10 | 4650 | 5741 | 2 | 2 | 2 | 2.015 |
| ele 3 | -3284 | -3293 | 10 | 4650 | 5741 | 2 | -2 | -2 | 2.015 |
| ele 4 | 0 | 0 | -4562 | 4562 | 6098 | -9 | -2 | 0 | 1.989 |
| ele 5 | 0 | 0 | 4562 | 4562 | 6098 | -9 | 2 | 0 | 1.989 |
| ele 6 | -162 | 330 | -4435 | 4450 | 1278 | -1 | -3 | 0 | 0.995 |
| ele 7 | -162 | -330 | 4435 | 4450 | -1278 | -1 | 3 | 0 | 0.995 |
When the angle of H-O-H is 90.0 degrees, the "octahedral" structure is more broken than 104.45 degrees.
So de Broglie's waves of electrons 2 and 3 is 0.015 different from 2.00.
(In case of 104.45 degrees, the difference is 0.011.)
When the angle becomes 90.0 degrees, the oxygen nucleus is repelled by the two hydrogen's nuclei to the left. (Fig.13)
(On the other hand, the electrons are attracted by them.)
So, to make the oxygen nucleus stable (= FX, FY, FZ of O nuc are small), we need to change the oxygen structure more than 104.45 degrees.
Fig. 13. Nuclei are repelled by each other.
Next we choose the angle "110.0" in the scrollbar, and click "angle" button.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 3138 | -3247 | 0 | 4515 | 5625 | -3 | -3 | -1 | 1.987 |
| ele 1 | 3138 | 3247 | 0 | 4515 | 5625 | -3 | 3 | 1 | 1.987 |
| ele 2 | -3290 | 3290 | -20 | 4652 | 5722 | 0 | 0 | 4 | 2.011 |
| ele 3 | -3290 | -3290 | 20 | 4652 | 5722 | 0 | 0 | -4 | 2.011 |
| ele 4 | 0 | 0 | -4556 | 4556 | 6116 | 1 | -4 | 0 | 1.989 |
| ele 5 | 0 | 0 | 4556 | 4556 | 6116 | 1 | 4 | 0 | 1.989 |
| ele 6 | -260 | 330 | -4650 | 4668 | 1182 | -4 | 2 | 0 | 0.994 |
| ele 7 | -260 | -330 | 4650 | 4668 | -1182 | -4 | -2 | 0 | 0.994 |
The number of de Broglie's waves of 110.0 degrees are almost same as that of 104.45 degrees.
But in case of 110.0 degrees, the total potential energy (tV = -936.85 eV) becomes higher than that of 104.45 degrees (-938.18 eV).
(Experimental value : tV = -939.84 eV )
So the bond strength is weaker in 110.0 degrees.
The e0 - O - e1 angle of the oxygen atom is 90 degrees due to the "octahedral" structure.
110.0 degrees is thought to be too large to form stable O-H bonds. (110 > > 90).
Next we choose the "104.45" degrees and click "angle" button. (=return to the original condition.) And then, we choose "9000" in the scrollbar, and click "O-H (MM)" button.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 3120 | -3240 | 0 | 4497 | 5471 | 0 | 0 | -1 | 1.983 |
| ele 1 | 3120 | 3240 | 0 | 4497 | 5471 | 0 | 0 | 1 | 1.983 |
| ele 2 | -3290 | 3290 | -20 | 4652 | 5720 | -1 | -1 | 4 | 2.010 |
| ele 3 | -3290 | -3290 | 20 | 4652 | 5720 | -1 | -1 | -4 | 2.010 |
| ele 4 | 0 | 0 | -4557 | 4557 | 6113 | 0 | -4 | 0 | 1.990 |
| ele 5 | 0 | 0 | 4557 | 4557 | 6113 | 0 | 4 | 0 | 1.990 |
| ele 6 | -260 | 310 | -4310 | 4328 | 1342 | 0 | 4 | 0 | 0.995 |
| ele 7 | -260 | -310 | 4310 | 4328 | -1342 | 0 | -4 | 0 | 0.995 |
Like the case of 90 degrees (Fig.13), when the O-H bond length is shorter than 9584 MM, the oxygen nuleus is repelled by the two hydrogen's nuclei.
So when the O-H bond length is 9000 MM, the "octahedral" structure is more broken for the stability of the oxygen nucleus.
As shown in Table 8, de Broglie's waves of electrons 0 and 1 are 1.983. (The error is -0.017.)
If you try to move the electrons 0 and 1 to make the value 1.983 closer to 2.00, the values 2.010 of electrons 2 and 3 becomes bigger instead. (For example, it becomes 2.016.)
So it can not change this "broken" structure. Try this,too.
(In this case, tV becomes -944.88 eV, which is lower than the experimental value -939.84 eV)
Next we choose "10000" in the scrollbar, and click "O-H (MM)" button.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 3150 | -3245 | 0 | 4522 | 5677 | 5 | 5 | -1 | 1.989 |
| ele 1 | 3150 | 3245 | 0 | 4522 | 5677 | 5 | -5 | 1 | 1.989 |
| ele 2 | -3290 | 3290 | -20 | 4652 | 5724 | 0 | 0 | 4 | 2.011 |
| ele 3 | -3290 | -3290 | 20 | 4652 | 5724 | 0 | 0 | -4 | 2.011 |
| ele 4 | 0 | 0 | -4558 | 4558 | 6104 | 1 | -4 | 0 | 1.989 |
| ele 5 | 0 | 0 | 4558 | 4558 | 6104 | 1 | 4 | 0 | 1.989 |
| ele 6 | -200 | 300 | -4800 | 4813 | 1118 | -7 | 6 | 0 | 0.995 |
| ele 7 | -200 | -300 | 4800 | 4813 | -1118 | -7 | -6 | 0 | 0.995 |
The numbers of de Broglie's waves in Table 9 are almost same as Table 5.
But when the O-H bond length is longer than 9584 MM, tV becomes higher (tV = -933.66 eV)
This means the bond strength is weaker.
You can try the other combinations of (9000 x 90 degrees), (9000 x 110 degrees ), (10000 x 90 degrees), and (10000 x 110 degrees).
In these combination, the proper initial condition is not automatically set up.
So you need to adjust the coordinates of electrons to make (fx, fy, fz) of each electron and (FX, FY, FZ) of O nucleus as small as possible. (less than 10, if possible.)
If you do this, you will know the case of Table 5 is the best condition.
In comparison to the methane (CH4), the hydrogen electrons (6,7) of H2O are closer to the oxygen nucleus.
(See Fig.10 and Fig.12.)
Fig. 14. The difference between C-H and O-H bond
So in H2O, the hydrogen bonds are thought to be formed with other molecules as shown in Fig.14.
Next we try NH3 molecular structure using the Virial theorem.
The average single N-H bond energy of NH3 is 4.052 eV (=391 kJ/mol).
So the total energy of NH3 is -266.94 (N) - 3 × 13.606 (H) - 3 × 4.052 (bond energy) = --319.914 eV.
(266.94 eV is the sum of 1-5th ionization energies.)
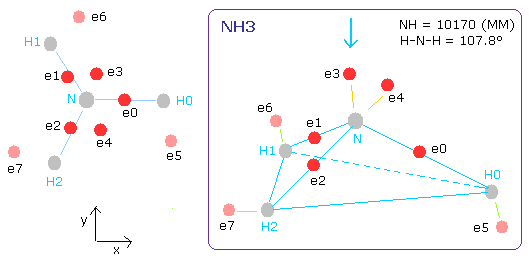
The N-H bond length of NH3 is 10170 MM (= 1.0170 × 10-10 meter).
The H-N-H angle is 107.8 degrees, which is a little smaller than 109.5 degrees (tetrahedron).
Fig. 15. Estimated ammonia (NH3) model.
In this nitrogen page, we have proved that the orbits of the nitrogen's five valence electrons are almost 2.0 de Broglie's wavelength.
In this section, we try to seek for ammonia (NH3) model which satisfies the Virial theorem and de Broglie's theory.
Sample JAVA program of NH3 (Virial theorem)
(In this program, the central charge is supposed to be +5.25e)
This program is a little long. So if you copy and paste the upper program source code into a text editor,
you can easily compile and run this.
This program's class file name is NH3, so save this text editor as "NH3.java", and compile it.
In this program, each particle of NH3 is shown on the x-y (left), x-z (center), and y-z (right) planes.
Here we use the new units, ( 1 MM = 10-14 meter).
Each coordinate of electrons (+X (MM), +Y (MM), +Z (MM)) in the text box means "relative" position from these nuclei.
(ele 0-4 are from nitrogen nucleus, ele 5 is from hydrogen nucleus 0 (H0), ele6 is from H1, and ele7 is from H2.)
You can change the coordinate (+X, +Y, +Z) freely.
(Enter the values into the textboxes, and press the Enter key.)
tV (eV) is the total potential energy.
CF of ele0-4 means the force toward the center, CF of ele5,6,7 means the force toward each N-H line.
(fx, fy, fz) mean force components other than CF.
(FX, FY, FZ) mean the force component acting on each nucleus.
Nf of H0 nucleus means the force toward N nucleus.
Waves (wn) is number of de Broglie's waves contained in one orbit.
when you choose the N-H bond length (MM) in the scrollbar and click "N-H (MM)" button, the internuclear distance of N-H change.
And when you choose the angle in the scrollbar and click "angle" button, H-N-H angle changes.
When you click "e5,6,7" button, electrons 5,6 and 7 are arrahnged "symmetrically".
the CF in NH3 includes the three hydrogen nuclei and electrons in addition to the nitrogen nucleus.
(In the program, array variables rpp[el][0-2] mean the force components toward CF, which is the total force from nitrogen nucleus, three hydrogen's nuclei and hydrogen's electrons.)
Fig. 16. Structure of NH3 (control. tV= -639.4 eV).
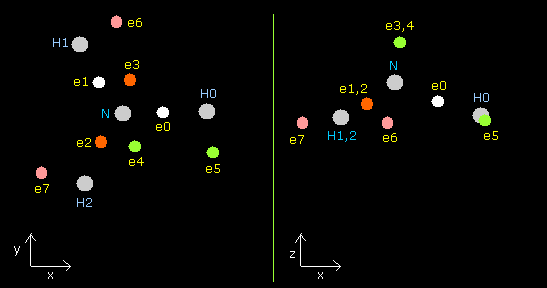
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 4870 | 0 | -2350 | 5407 | 3000 | 1 | 0 | 2 | 2.002 |
| ele 1 | -2685 | 3685 | -2488 | 5194 | 3508 | 4 | 0 | -3 | 1.988 |
| ele 2 | -2685 | -3685 | -2488 | 5194 | 3515 | 4 | -1 | -2 | 1.988 |
| ele 3 | 595 | 3780 | 3950 | 5499 | 3545 | -13 | -8 | 9 | 2.011 |
| ele 4 | 595 | -3780 | 3950 | 5499 | 3547 | -12 | 8 | 9 | 2.011 |
| ele 5 | 340 | -4380 | -370 | 4408 | 1230 | -190 | 0 | 77 | 0.998 |
| ele 6 | 3790 | 2506 | -400 | 4561 | 1185 | 104 | -183 | 64 | 0.996 |
| ele 7 | -4020 | 1770 | -450 | 4415 | -1228 | 98 | 175 | 116 | 0.996 |
Due to the repulsive force of three hydrogen nuclei, de Broglie's waves become a liitle different from 2.00 in electrons 0-4 to make the nitrogen nucleus stable (in which FX, FY, FZ of N nuc are small).
In Table 10, the total potential energy (tV) becomes -639.4 eV, which is almost same as the experimental value (= 2 × -319.914 = -639.82 eV)
The electrons 5-7 are a little outside of hydrogen nucleus (Fig.16), so (fx,fy,fz), which are other than CF force (toward N-H line) is not zero in electrons 5-7.
They are more outside than H2O (See Fig.12), but more inside than CH4 (See Fig.10).
Fig. 17. Comparison of C-H, O-H, and N-H bonds.
Next we choose "100.0" in the scrollbar, and click "angle" button.
Automatically, the proper initial condition is set up.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 4820 | 0 | -2510 | 5434 | 2934 | -5 | -1 | -10 | 2.002 |
| ele 1 | -2695 | 3685 | -2570 | 5239 | 3368 | 13 | 2 | -11 | 1.988 |
| ele 2 | -2695 | -3685 | -2570 | 5239 | 3368 | 12 | -2 | -11 | 1.988 |
| ele 3 | 616 | 3780 | 3940 | 5494 | 3565 | -11 | -7 | 9 | 2.022 |
| ele 4 | 600 | -3780 | 3940 | 5492 | 3569 | -10 | 8 | 9 | 2.021 |
| ele 5 | 350 | -4280 | -370 | 4310 | 1279 | -209 | 0 | 83 | 0.996 |
| ele 6 | 3680 | 2500 | -440 | 4470 | 1222 | 119 | -209 | 92 | 0.997 |
| ele 7 | -4000 | 1700 | -450 | 4369 | 1244 | 107 | 186 | 117 | 0.996 |
When the H-N-H angle is smaller than 107.8 degrees, the repulsive upward force of three hydrogen nuclei becomes stronger. (See Fig.15).
So, to make the nitrogen nucleus stable, "symmetrical" distribution of nitrogen electrons 0-4 are more broken than the case of 107.8 degrees.
As showon in Table 11, de Broglie's waves of electrons 3 and 4 becomes larger. (The error is +0.022).
If you try to decrease this value from 2.022, the waves of electrons 1 and 2 become smaller than 1.988 instead.
So this error would not be decreased. Try this, too.
Next we choose "110.0" in the scrollbar, and click "angle" button.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 4880 | 0 | -2380 | 5429 | 2990 | 7 | 0 | 14 | 2.003 |
| ele 1 | -2695 | 3685 | -2470 | 5190 | 3538 | -1 | 3 | 6 | 1.989 |
| ele 2 | -2695 | -3685 | -2470 | 5190 | 3556 | -1 | -3 | 6 | 1.989 |
| ele 3 | 650 | 3780 | 3940 | 5498 | 3549 | -19 | -7 | 10 | 2.011 |
| ele 4 | 650 | -3780 | 3940 | 5498 | 3551 | -18 | 7 | 10 | 2.011 |
| ele 5 | 290 | -4400 | -370 | 4425 | 1222 | -172 | -1 | 77 | 0.998 |
| ele 6 | 3820 | 2600 | -350 | 4634 | 1155 | 107 | -186 | 60 | 0.995 |
| ele 7 | -4020 | 1800 | -450 | 4427 | 1225 | 95 | 170 | 117 | 0.995 |
In the case of 110.0 degrees, de Broglie's waves are almost same as the control of Table 10.
But the total potential energy (tV) becomes higher (= -637.98 eV) than the control (= -639.4 eV).
(Experimental value of tV is -639.82 eV)
So this case is more unstable.
Next we choose "107.8" and click "angle" button, which returns to the first condition.
And then we choose "9000" and click "N-H (MM)" button.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 4800 | 0 | -2160 | 5263 | 2600 | 7 | 0 | 14 | 1.981 |
| ele 1 | -2540 | 3750 | -2400 | 5125 | 3139 | 0 | 5 | 7 | 1.986 |
| ele 2 | -2540 | -3750 | -2400 | 5125 | 3177 | 0 | 0 | 0 | 1.987 |
| ele 3 | 490 | 3800 | 4150 | 5648 | 3337 | -9 | 2 | -1 | 2.025 |
| ele 4 | 450 | -3800 | 4100 | 5608 | 3399 | -5 | 3 | 3 | 2.014 |
| ele 5 | 800 | -4200 | -500 | 4304 | 1236 | -383 | 0 | 139 | 0.998 |
| ele 6 | 3470 | 2480 | -440 | 4287 | 1288 | 159 | -280 | 96 | 0.995 |
| ele 7 | -3700 | 1545 | -450 | 4034 | 1396 | 143 | 254 | 162 | 0.999 |
In the case of 9000 MM, due to the stronger repulsive nuclear force, the nitrogen structure becomes more broken.
So the error of de Broglie's waves becomes larger (+0.025 of ele3 and -0.019 of ele0 in Table 13.) in comparison with Table 10.
In this case, the total potential energy is -655.22 eV, which is much lower than the experimental value (-639.98 eV).
And the force toward N nucleus of H0 nuclues (=Nf) is too big (= 536), which shows the hydrogen nucleus is unstable.
Next we choose "11000" and click "N-H (MM)" button.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 4870 | 0 | -2300 | 5385 | 3282 | -4 | 0 | -8 | 2.002 |
| ele 1 | -2695 | 3660 | -2550 | 5211 | 3661 | 5 | 0 | -6 | 1.986 |
| ele 2 | -2695 | -3650 | -2560 | 5209 | 3670 | 6 | 0 | -5 | 1.986 |
| ele 3 | 530 | 3740 | 3940 | 5458 | 3588 | -9 | -3 | 4 | 2.006 |
| ele 4 | 520 | -3740 | 3940 | 5457 | 3591 | -9 | 2 | 3 | 2.007 |
| ele 5 | 220 | -4480 | -260 | 4492 | 1222 | -130 | 0 | 50 | 0.994 |
| ele 6 | 3890 | 2400 | -300 | 4580 | 1196 | 69 | -122 | 42 | 0.993 |
| ele 7 | -4000 | 2026 | -300 | 4493 | 1221 | 54 | 97 | 76 | 0.993 |
In the case of 11000 MM, de Broglie's waves are relatively stable.
But the total potential energy (tV) becomes higher (= -635.67 eV) than the control of Table 10 (= -639.4 eV)
This means the bond strength becomes weaker in this 11000 MM.
You can try the other combinations of (9000 x 100 degrees), (9000 x 110 degrees ), (11000 x 100 degrees), and (11000 x 110 degrees).
In these combination, the proper initial condition is not automatically set up.
So you need to adjust the coordinates of electrons to make (fx, fy, fz) of each electron and (FX, FY, FZ) of N nucleus as small as possible. (less than 10, if possible.)
If you do this, you will know the case of Table 10 (control) is the best condition.

2010/11/20 updated. Feel free to link to this site.