
曽埵慄偵偮偄偰
戝榓嶰嶳偲嶰椫嶳
60搙慄偲孎栰
惛搙傪峫偊傞
懢梲偺摴
曽埵慄偺娭悢
丂
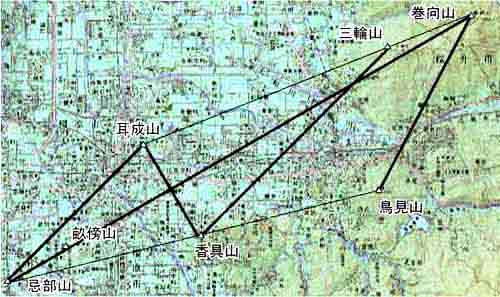
丂360搙偳偙傪偲偭偰傕曽埵慄偱偡偑丄杮榑偱偄偆曽埵慄偲偼搶惣慄偍傛傃偦傟偵懳偡傞30搙丒45搙丒60搙丒90搙(撿杒慄)偺奺曽埵慄偺偙偲偱偡丅偙傟傜偺曽埵慄偑壗傜偐偺堄枴傪帩偭偰偄傞傜偟偄偲姶偠偰傕傜偆偨傔偵丄偙偆偄偆応崌偺掕斣偱偁傞嶰椫嶳偲戝榓嶰嶳傪庢傝忋偘偰傒傑偡丅嶰椫嶳傗楈奅捠怣偲戝榓嶰嶳偺婔壗妛揑娭學偵偮偄偰偼丄偄傠偄傠側妏搙偐傜庢傝忋偘傜傟偰偄傑偡偑丄偙偙偱偼傑偢帹惉嶳丒嶰椫嶳丒姫岦嶳丄姫岦嶳丒悿朤嶳丒婖晹嶳丄婖晹嶳丒崄嬶嶳丒捁尒嶳(俀俆係m嶰妏揰)偑偦傟偧傟捈慄傪嶌偭偰丄倅帤宍偵側偭偰偄傞偙偲偵拲栚偟傑偡丅
丂丂帹惉嶳乮0.01搙乯乗嶰椫嶳乗姫岦嶳乮0.04搙乯偺捈慄
丂丂姫岦嶳乮0.31搙乯乗悿朤嶳乗婖晹嶳乮2.32搙乯偺捈慄
丂丂婖晹嶳乮0.77搙乯乗崄媣嶳乗捁尒嶳乮0.77搙乯嶰妏揰偺捈慄
偦偆偡傞偲丄偙傟傜偺彅嶳傪寢傇師偺傛偆側曽埵慄偑峫偊傜傟傞偺偱偡丅
丂丂嶰椫嶳乗崄媣嶳乮W0.047km丄0.43搙乯偺搶杒45搙慄
丂丂崄媣嶳乗帹惉嶳乮E0.032km丄0.77搙乯偺惣杒60搙慄
丂丂帹惉嶳乗婖晹嶳乮W0.043km丄0.55搙乯偺搶杒45搙慄
丂丂姫岦嶳乗悿朤嶳乮E0.028km丄0.15搙乯乗婖晹嶳乮W0.034km丄0.16搙乯偺搶杒30搙慄
丂丂姫岦嶳乗捁尒嶳嶰妏揰乮E0.037km丄0.46搙乯偺搶杒60搙慄
丂悢帤偺尒曽偱偡偑丄曽埵慄偼悢帤偺側偄応強傪捠傞曽埵慄傪婎弨偵偟偰丄悢帤偺偁傞応強傪捠傞曽埵慄偑搶惣偁傞偄偼撿杒偑偳偪傜懁偵偁傞偐傪傾儖僼傽儀僢僩偱丄嫍棧傪帵偡悢帤偼擇偮偺応強傪捠傞曽埵慄偑杒堒35搙晅嬤偱偮偔傞暆丄妏搙偼擇偮偺応強傪寢傫偩幚嵺偺曽埵慄偑婯掕偺曽埵慄偐傜偳偺偔傜偄偢傟偰偄傞偐傪丄娙棯揑側曽朄偱寁嶼偱摼傜傟傞偍偍傛偦偺悢帤偲偟偰昞偟偰偄傑偡丅傑偨丄嵟屻偵扨偵暆偺悢帤偟偐弌偰偙側偄傕偺傕弌偰偒傑偡偑丄偦傟偼俁偮埲忋偺揰偱偮偔傞曽埵慄偱丄偦傟傜偺偆偪偺擇揰偑嶌傞曽埵慄偺偆偪嵟戝偺暆偺傕偺傪帵偟偰偄傑偡丅捈慄偺傎偆偼丄挿偝偑嵟戝偺擇揰傪婎弨偵偦偺椉懁偱恀拞偺応強偲偮偔傞妏搙偱偡丅恀拞偵嫍棧傪偁傜傢偡悢帤偑弌偰偔傞応崌偼丄恀拞偺抧揰偐傜奜懁偺抧揰傪寢傫偩慄傑偱偺嫍棧偱偡丅偙傟偑彫偝偡偓傞偲丄僄僋僙儖偺惛搙偺斖埻傪挻偊傞偣偄偐偆傑偔寁嶼偝傟傑偣傫丅側偍丄亇傗丠偺晅偄偨傕偺傕弌偰偒傑偡偑丄亇偼応強傪惓妋偵抧恾忋偱摿掕偱偒側偄応崌乮悢昐儊乕僩偖傜偄偼傒偰偔偩偝偄乯丄丠偼偨偲偊偽棯恾傗婰弎偐傜抧恾忋偺偦偺恄幮偱娫堘偄側偄偲巚傢傟偰傕嵟廔妋擣偱偒偰偄側偄偽偁偄偱偡乮偙傟傜偼晅偗朰傟偰偄傞応崌偑偁傞偐傕偟傟傑偣傫乯丅偝傜偵曽埵丒曽埵慄偵偨偄偟偰曽岦丒曽岦慄偲偄偆尵梩傕弌偰偒傑偡偑丄偙傟偼曽埵慄偵斾傋偰惛搙揑偵傛傝娒偔偟偨傕偺偱偡丅
丂
丂搶惣慄傗30搙慄偼擇帄擇暘慄偲偟偰懢梲嵳釰側偳偲娭學偟偰丄45搙慄偼婼栧丒棤婼栧傗恄栧丒棤恄栧側偳偲偟偰丄撿杒慄偼媨搒偺拞怱幉側偳偲偟偰丄偦傟偧傟廳梫側曽岦偲偟偰偁傞偙偲傕棟夝偱偒傑偡偑丄60搙慄偼偦傟傎偳廳梫偲傕巚偊側偄偐傕偟傟傑偣傫丅偟偐偟丄曽埵慄偲偟偰60搙慄偑柍帇偱偒側偄偺偼丄偨偲偊偽孎栰偱傕曽埵慄娭學偑尒傜傟傑偡偑丄偦偺拞偱傕60搙慄偑廳梫側曽埵偲側偭偰偄傞偙偲偐傜傢偐傝傑偡丅
丂孎栰偱傑偢栚偵偮偔偺偼丄孎栰嶰嶳偲偄傢傟傞杮媨丒怴媨丒撨抭偺偆偪丄柧帯帪戙偵峖悈偱尰嵼抧偵堏揮偡傞慜偺捔嵗抧偱偁傞偲偄偆杮媨偺戝嵵尨丄孎栰懍嬍戝幮媦傃孎栰懍嬍戝幮偑偦偙偐傜堏偭偨偲偄偆恄憅嶳偺僑僩價僉娾丄偦傟偵撨抭偺戝戧偑曽埵慄偱寢偽傟偰偄傞偙偲偱偡丅
丂丂
丂丂撨抭偺戝戧乗戝嵵尨乮W0.253km丄0.72搙乯偺惣杒60搙慄
丂丂戝嵵尨乗孎栰懍嬍戝幮乮W0.148km丄0.38搙乯偺惣杒30搙慄
丂丂孎栰懍嬍懍嬍戝幮乮E0.037km丄1.97搙乯乗僑僩價僉娾偺撿杒慄
丂丂僑僩價僉娾乮W0.105km丄0.6搙乯乗撨抭偺戝戧偺搶杒30搙慄
丂偙偙偱偼丄60搙慄傕弌偰偒傑偡偑丄30搙慄偺傎偆偑懡偄偲偄偊傑偡丅偟偐偟丄偙傟傜偵孎栰嶰嶳偺墱偺媨偲偄傢傟傞嬍抲恄幮傪擖傟傞偲丄師偺傛偆偵60搙慄偑栚棫偭偰偒傑偡丅
丂丂嬍抲恄幮乗戝嵵尨乮E0.485km丄2.47搙乯偺搶杒60搙慄
丂丂嬍抲恄幮乗僑僩價僉娾乮E0.89km丄1.95搙乯偺惣杒60搙慄
丂嬍抲恄幮偲戝嵵尨偺曃妏偑戝偒偄傛偆偵傕巚偊傑偡偑丄偦偺栤戣偼屻偱峫偊傞偲偟偰丄偙偺60搙慄偵偮偄偰偼丄偝傜偵僑僩價僉娾偲壴偺孉偺搶杒60搙慄偑峫偊傜傟丄偦傟偼孎栰偲偼偄偊側偄偐傕抦傟傑偣傫偑丄尦埳惃偺堦偮戧尨媨偵傑偱墑偽偡偙偲偑偱偒傑偡丅戧尨媨偲孎栰偲偺娭學偑柍帇偱偒側偄偺偼丄杮媨戝嵵尨偲傕搶杒45搙慄傪嶌傞偙偲偐傜傕偄偊傑偡丅戧尨媨偲孎栰偺曽埵慄偼弌塤恄懓偺偲偙傠偱峫偊偰偰傒偨偄偲巚偄傑偡偑丄僀僓僫儈偺曟偲傕偄傢傟傞壴偺孉偵偮偄偰嫽枴怺偄曽埵慄傪傂偲偮偁偘傞側傜丄偦傟偑扺楬搰偺埳淨戻恄媨偲惣杒30搙慄傪偮偔傞偙偲偱偡丅
丂丂僑僩價僉娾乗壴偺孉乮E0.03km丄0.09搙乯乗戧尨媨乮E0.516km丄0.36搙乯偺搶杒60搙慄
丂丂杮媨戝嵵尨乗戧尨媨(E0.573km丄0.39搙乯偺搶杒45搙慄
丂丂壴偺孉乗埳淨戻恄媨乮W1.219km丄0.54搙乯偺惣杒30搙慄
丂戧尨媨偼僑僩價僉娾傛傝孎栰懍嬍戝幮乮E0.012km丄0.01亱乯偲偺曽偑惓妋側搶杒60搙慄傪偮偔傝傑偡偑丄僑僩價僉娾傪偲傝偁偘偨偺偼丄孎栰尃尰偺墢婲偵傛傟偽丄孎栰尃尰偼婭埳崙偱偼嵟弶偵柎楰孲愗晹嶳(愗栚)偺惣偺嬍撨栘偺暎偵崀傝丄偦偙偐傜恄憼曯丄師偵垻恵夑幮偺杒偺愇暎偺扟偵堏傝丄偦偙偐傜悞恄挬偵杮媨丄宨峴挬偵尰嵼偺怴媨懍嬍戝幮偺抧偵堏偭偨偲偁偭偰丄怴媨幮偑堦斣怴偟偄偲偄偆偙偲偵側傝丄偙偺怴媨幮憂寶埲慜偵傕怴媨偺抧偲壴偺孉丒戧尨媨傪寢傇曽埵慄偑偁偭偨偙偲傪尵偄偨偐偭偨偐傜偱偡丅孎栰尃尰偺婳愓傪傒傞偲丄愗晹嶳偡側傢偪報撿挰偺愗栚墹巕嬤曈偼杮媨傗怴媨偺傎傏惣偱偡偑丄惓妋側搶惣慄傪嶌偭偰偼偄傑偣傫丅偟偐偟丄恄憅嶳偺僑僩價僉娾偲垻恵夑恄幮恄懱嶳偺晣梪嶳偲偼搶杒30搙慄傪嶌傝傑偡丅偡側傢偪丄撨抭偺戝戧偲僑僩價僉娾偦傟偵晣梪嶳偑堦偮偺曽埵慄傪嶌偭偰偄傞傢偗偱偡丅晣梪嶳偲杮媨戝嵵尨傕惣杒30搙慄傪嶌傝傑偡丅
丂丂僑僩價僉娾乗垻恵夑恄幮晣梪嶳(W0.015km丄0.58搙)偺搶杒30搙慄
丂丂杮媨戝嵵尨乗垻恵夑恄幮朒棄嶳(E0.171km丄0.42搙)偺惣杒30搙慄
丂曽埵慄偺幚懺偲偼壗側偺偐偵偮偄偰偼丄巆擮側偑傜崱偺偲偙傠暘偐傝傑偣傫丅傑偭偨偔偺尪憐偲偄偆偙偲傕偁傝偊傞傢偗偱偑丄摉慠偙偙偱偼曽埵慄偑偁傞偲傒側偟偰偄傑偡丅偨偩丄偦偺曽埵慄忋偵偁傞憤偰偺傕偺偑曽埵慄偲娭學偟偰偄傞偲偼偄偊側偄偐傕抦傟傑偣傫丅偙偺応崌丄揝摴傪峫偊偰傒傟偽棟夝偟傗偡偄偐傕偟傟傑偣傫丅揝摴偺応崌丄慄楬偑捠偭偰偄傞偩偗偱墂偑柍偗傟偽壗偺堄枴傕偁傝傑偣傫偑丄曽埵慄偺応崌傕丄墂偲側傞億僀儞僩偐偳偆偐偑廳梫側傢偗偱偡丅傑偨丄揝摴偵偼媫峴丒摿媫傗摿暿楍幵偺傛偆偵摿掕偺墂偟偐掆傑傜側偄傕偺傕偁傝傑偡偑丄傕偟偐偟偨傜曽埵慄偵傕偦偺傛偆側偙偲偑偁傞偐傕偟傟傑偣傫丅扨偵曽埵慄忋偵偁傞偩偗偱偼側偔偰丄傛傝擺摼偱偒傞棟桼偑昁梫側傢偗偱偁傝丄壗傜偐偺暔岅惈偑媮傔傜傟傢偗偱偡丅偨偩丄憤偰偺応強偵偍偄偰丄偦偺棟桼偑柍偄偺偱偼側偔偰敪尒偱偒偰偄側偄丄偁傞偄偼偦偺棟桼偑崱偱偼朰傟嫀傜傟偰偟傑偭偰偄傞丄偲偄偆壜擻惈傕傑偨偁傞傢偗偱偡丅
丂曽埵慄傗儗僀儔僀儞偲偄偭偨応崌丄昁偢嬼慠偐偳偆偐偑栤戣偵側傝傑偡丅偱偼丄悢妛揑偵摎偊傪弌偣傞偺偐偲偄偆偲丄幚幙揑偵晄壜擻偱偡丅偨偲偊偽恄幮傪峫偊傞応崌丄幮揳偺戝偒偝傪10儊乕僩儖巐曽偲偟傑偡丅偦偆偡傞偲丄抧恾傪10儊乕僩儖巐曽偺儅僗偵嬫愗偭偰丄偦傟偧傟偺儅僗偺抧宍傪挷傋丄屛偺恀傫拞偲攇懪偪嵺丄偁傞偄偼媫幬柺偲暯抧傪摨偠忦審偲偡傞偺偼偍偐偟偄偱偡偐傜丄抧宍偛偲偵僂僃乕僩傪偐偗側偗傟偽側傝傑偣傫丅僒儞僾儖傪嵦傝丄偦偙偐傜偁傞掱搙偺僂僃乕僩抣偼弌偰偔傞偐傕偟傟傑偣傫(偦傟帺懱朿戝側嶌嬈検偑梊憐偝傟傞)偑丄偦傟偼傕偆嬤帡抣偱偡偟丄惓妋偵抧宍傪摉偰偼傔傛偆偲偡傟偽抧恾忋偩偗偱側偔幚抧専暘偟側偗傟偽側傝傑偣傫偐傜丄幚嵺偵10儊乕僩儖巐曽偺儅僗偵抧宍傪妱傝摉偰偰偄偔嶌嬈偼偦傫側偵峀偔側偄抧堟偵尷偭偰傕晄壜擻偱偟傚偆丅
丂偦傟偱傛傝娙棯壔偟偰丄嶰売強偑曽埵慄偱寢偽傟偰偄傞偲偄偆扨弮側応崌傪峫偊偰傒傑偡丅偦偺嶰売強傪俙俛俠偲偟丄俠偑俙俛偐傜曃妏兛偱曽埵慄倎丄倐偲寢偽傟傞妋棪偼丄倎倐偦傟偧傟偵曃妏兛偲側傞擇偮偺捈慄傪堷偒丄偦偺俀杮偺慄偱偼偝傑傟偨晹暘偺偆偪丄廳側傞晹暘偺柺愊傪媮傔丄峫偊偰偄傞椞堟偺柺愊偱妱偭偨傕偺偲偄偆偙偲偵側傝傑偡丅偡側傢偪丄嶰揰偑曽埵慄偱寢偽傟傞妋棪偼丄俙俛偑曽埵慄傪嶌傞妋棪傪媮傔丄師偵椞堟撪偱俙俛傪捠傞曽埵慄偺慻崌偣偺嶌傞廳側偭偨晹暘偺柺愊偺榓傪椞堟柺愊偱妱偭偨悢帤傪妡偗偨傕偺偑偦偺妋棪偲偄偆偙偲偵側傝傑偡丅慜偵栤戣偵偟偨杮媨戝嵵尨偲嬍抲恄幮偺曃妏2.47搙偱峫偊偰傒傑偡偲丄暋嶨側寁嶼偑昁梫側応崌偼妋棪偑崅偔側傞傛偆偵張棟偟偰丄俙俛偺拞揰傪拞怱偵丄敿宎傪俙俛偺挿偝偲摨偠墌傪椞堟柺愊偲偟丄奺曽埵慄偵偮偒寁嶼偟傑偡偲丄婋尟棪1.7亾庛丄1.5攞偺応崌傕1.7亾庛丄擇攞傪敿宎偲偟偨応崌偼1.9亾庛偲偄偆偙偲偵側傝傑偡丅偙傟偼丄嵟掅婎弨偱偁傞婋尟棪俆亾埲撪傪桳堄偲峫偊傟偽丄偦偺斖埻撪偵廂傑傞悢帤偱偡偐傜丄応崌偵傛偭偰偼嬼慠偱偼側偄偲傕庡挘偱偒傞傢偗偱偡丅偨偩丄偦偺偨傔偵偼摉偰偼傑傞忦審偺応強偑偦偺嶰売強偺傒偱丄偦偺嶰売強偑婋尟棪俆亾偵廂傑傞傛偆側曃妏偱(曃妏2.47搙亄兛乺埲撪偱偦傟偧傟曽埵慄傪嶌偭偰偄傞傛偆側嬶懱椺偑昁梫偲側傝傑偡丅傕偟偦偺傛偆側嬶懱椺偑偁傟偽丄曽埵慄偺婡擻帺懱偼偳偺傛偆側応崌傕曄傢傜側偄偲峫偊傜傟傑偡偐傜丄嬍抲恄幮偲戝嵵尨傕曽埵慄偑惉傝棫偮偲傒側偡偙偲傕壜擻側傢偗偱偡丅
丂巆擮側偑傜丄孎栰偱偼偦偺傛偆側嶰妏宍傪尒偮偗弌偡偙偲偼偱偒傑偣傫丅撨抭偺戝戧丒戝尨搾丒懍嬍恄幮丒僑僩價僉娾偼曽埵慄偱寢偽傟偨巐妏宍傪偮偔偭偰偄傑偟偨偑丄偦傟偼嶰妏宍偱偼偁傝傑偣傫偟丄懳徾偲偡傞応強偑偦傟傜巐売強偵尷掕偱偒傞偲偄偆忦審偑偁傝傑偣傫丅孎栰偱偁傞掱搙擺摼偱偒丄懳徾売強偑尷掕偱偒傞忦審傪偁偘傟偽丄傑偢孎栰嶰嶳偲偄偆偖傜偄偱偡偐傜丄撨抭偺戝戧丒戝嵵尨丒懍嬍戝幮偑峫偊傜傟傑偡丅偦傟偵丄墱偺媨偲偝傟傞嬍抲恄幮傕壛偊傞偙偲偑偱偒傞偐傕偟傟傑偣傫丅傕偆傂偲偮偼丄孎栰尃尰偑孎栰偱堏摦偟偨偲偄偆丄恄憅嶳偺僑僩價僉娾丒垻恵夑恄幮偺晣梪嶳丒戝嵵尨丒懍嬍戝幮偺僙僢僩偱偡丅偙偺擇偮偺僙僢僩偼孎栰怣嬄偺堦晹暘偱丄擇偮傪崌傢偣偰堦偮偺慡懱偲峫偊傞偙偲傕偱偒傞偐傕偟傟傑偣傫丅偦偆偡傞偲丄懳徾斖埻偑撨抭偺戝戧丒戝嵵尨丒僑僩價僉娾丒垻恵夑恄幮偺晣梪嶳丒孎栰懍嬍戝幮丒嬍抲嶳偲偄偆僌儖乕僾偑弌棃忋偑傞栿偱偡丅偙偺俇儠強傪曽埵慄偺偮側偑傝偱傒傑偡偲丄曽埵慄偱偮側偑傝丄偦傟偑暵偠偨椫偵側偭偰偄傞偙偲偑暘偐傝傑偡丅偦偺傛偆側暵偠偨椫偱堦斣扨弮側偺偼榋妏宍偲丄巐妏宍偲嶰妏宍偑堦揰偱偮側偑偭偨擇偮偺宍偵側傝丄偦傟偧傟偺僷僞乕儞偼60偲180傪挻偊側偄偙偲偼偡偖暘偐傝傑偡丅偙偺傛偆側宍懺偑曃妏2.47搙偱壜擻側妋棪傪媮傔傑偡偲丄僷僞乕儞悢傪60偲180偲偟偰丄偁傞揰偵懳偟偁傞揰偑曽埵慄傪嶌傞妋棪傪8亊2.49/90丄偁傞揰偑懠偺擇揰偲曽埵慄傪嶌傞妋棪傪7.4亾偲偟偰丄寁嶼偡傞偲丄婋尟棪2.1亾庛偱桳堄偲偄偆偙偲偵側傝傑偡丅偁傞揰偑擇揰偲曽埵慄傪嶌傞妋棪偼丄擇揰偺忬懺偱堎側傝傑偡偑丄慜婰偺曽埵慄嶰妏宍偱巊偭偨偄偔偮偐偺椺偱偼丄4.5乣7.4亾丄暯嬒5.3亾偲偄偆偙偲偱丄偙偺偆偪偺嵟戝7.4亾傪巊偆偙偲偵偟傑偟偨丅偙傟傜偺悢帤偼偁偔傑偱傕堦偮偺栚埨偵偡偓傑偣傫丅傕偭偲傕丄傑偭偨偔峳搨柍宮偺榖偱偼側偄偲偄偆偙偲傪擺摼偝偣傞偙偲偵偼丄彮偟偼栶棫偮偐傕偟傟傑偣傫偑丅
丂晛捠媄弍偑崅傑傞偲偦傟偵楢傟偰嫍棧揑丒妏搙揑惛搙傕崅傑傞偲峫偊偰偟傑偄傑偡偑丄昁偢偟傕偦偆偲偼尷傝傑偣傫丅妋偐偵丄應検側偳傪峫偊傞偲偦偆偄偊傞偐傕偟傟傑偣傫偑丄椺偊偽帴椡慄扵抦婡側偳傪峫偊傑偡偲丄偦傟偼惈擻偑忋偑傞傎偳旝庛側曄壔偵傕斀墳偟傑偡偐傜丄揹慄偐傜傛傝墦偔棧傟偨偲偙傠偱傕曄壔傪扵抦偱偒傞傛偆偵側傞偼偢偱偡丅曽埵慄傪峫偊傞応崌丄偦傟傪應検宆偱懆偊傞偐扵抦宆偱懆偊傞偐偱曽埵慄偺惛搙偵懳偡傞峫偊曽偑傑偭偨偔曄傢偭偰偔傞傢偗偱偡丅應検宆偐扵抦宆偐偼丄曽埵慄偦偺傕偺偺惈幙偑柧傜偐偵側傜側偄尷傝偳偪傜傪慖傫偩傜偄偄偐暘偐傜側偄榖偱偡偑丄嫮椡偱崅惈擻側曽埵慄傎偳丄偦偺惛搙偼埆偔側傞壜擻惈傕偁傞傢偗偱偡丅傕偭偲傕丄屆戙偵壗傜偐偺暔棟揑扵抦憰抲偑偁偭偨偲傕峫偊傜傟傑偣傫偐傜丄偙偺応崌偼堦庬偺戞榋姶揑側傕偺偑巊梡偝傟偨偲偄偆偙偲偵側傝傑偡丅應検宆偱偼曃妏偑丄扵抦宆偱偼曽埵慄偐傜偺嫍棧偑栤戣偵側傞偲偄偊傞偐傕偟傟傑偣傫丅嫍棧偑栤戣側傜丄曃妏偑戝偒偔偰傕嫍棧揑偵曽埵慄偲傒側偣傞応崌傕偁傞傢偗偱偡丅偙偺応崌丄嬤応偱偼丄曽岦揑偵偼偲傫偱傕側偄曽岦偱傕丄曽埵慄偵斀墳偟偰偟傑偆偙偲偑偁傝偊傞傢偗偱偡丅傕偟偐偟偨傜丄應検宆偲扵抦宆偑旝柇偵棈傒崌偭偨宍偱曽埵慄偲偄偆傕偺偑偁傞偺偐傕偟傟傑偣傫丅傑偨丄幚嵺偵偼應検偵傛偭偰寛掕偝傟偨曽埵慄娭學傕扵抦宆偵傛偭偰寛掕偝傟偨曽埵慄娭學傕椉曽偁傞偲傒側偡傋偒偱偟傚偆丅
丂惛搙偱傕偆堦偮峫偊側偗傟偽側傜側偄偙偲偼丄曽埵慄偺傒偑廳梫偱偼側偄偲偄偆偙偲偱偡丅椺偊偽丄恄幮傪峫偊偰傒傞偲丄偦偺埵抲偺寛掕偵偼嶳偺忋偲偐丄嬤偔偵斨嵗偲側傞嫄愇傗惔悈偑桸偄偰偄傞応強偲偐丄偦偺懠條乆側忦審偑峫偊傜傟傑偡丅曽埵慄偺桪愭弴埵偼掅偄壜擻惈偝偊偁傝傑偡丅偦偆偡傞偲丄懠偺忦審丒梫慺傕壛枴偟偨寢壥丄幚嵺偺恄幮偺応強偼曽埵慄偑惉傝棫偮斖埻偱偳傫偳傫墦偔偺応強偑慖偽傟偰偄偔偲偄偆壜擻惈傕偁傞傢偗偱偡丅偙偺応崌丄扵抦宆偱偡偲丄惈擻偑傛偔側傟偽側傞傎偳棧傟偐偨偑戝偒偔側傞傢偗偱偡丅
丂廰扟栁堦巵偼亀嫄戝屆暛偺惞掕亁偵偍偄偰丄幚嵺偵偼愜傟嬋偑偭偰偄偰捈慄偲偼偄偊側偄偙偲偲丄椉椬偺杒堒34搙31暘偲33暘偲偝偊斾傋偰傕屆戙堚愓偑彮側偄偙偲偐傜乽懢梲偺摴乿偼懚嵼偟側偄偲偄偄傑偡丅偟偐偟丄偙傟傑偱尒偰偒偨傛偆偵戝偒側曃妏偱傕栤戣側偄偺偩偲偡傟偽丄彮側偔偲傕愜傟嬋偑偭偰捈慄偲偼偄偊側偄丄偲偄偆偙偲偼乽懢梲偺摴乿偺斲掕偺崻嫆偵偼側傜側偄偲偄偆偙偲偵側傝傑偡丅偁偲偼丄堚愓悢偺栤戣偱偡偑丄廳梫側偙偲偼暔岅惈偲偱傕偄偊傞傕偺偱丄乽懢梲偺摴乿偱偼懢梲怣嬄偑暔岅偺妀怱偱偡偐傜丄杒堒34搙31暘傗33暘偺堚愓偑偳偺偖傜偄懢梲嵳釰偲娭學偟偰偄傞偐丄偁傞偄偼懠偺暔岅偲娭學偟偰偄傞偐丄偦偺応崌32暘偺乽懢梲偺摴乿偵斾傋偰懡偄偺偐彮側偄偺偐偑栤戣偵側傝傑偡丅
丂惛搙偑崅偄偲偄偆偺偼丄堦偮偵偼旕忢偵婥帩偪偑偄偄偟丄傑偨丄悢妛揑偵傕偦傟偑嬼慠偱偼側偄壜擻惈偑崅傑傞傛偆側婥偑偟偰偟傑偄傑偡偑丄応崌偵傛偭偰偼媄弍揑尷奅傪偼傞偐偵挻偊偨惛搙傪昁梫偲偡傞偙偲偵側傝丄寢壥偦偺徹柧偑傑偭偨偔堄枴傪側偝側偔側傞偲偄偆偙偲傕偁傝偊傞偐傕偟傟傑偣傫丅廰扟栁堦巵偺偁偘傞惛搙偼丄堒搙宱搙偵娭偟偰偼0.5昩偱12乣15儊乕僩儖丄嫍棧偼0.5亾埲撪丄曽埵妏0.3搙埲撪乮恀杒婎弨乯丄憡懳妏0.2搙埲撪偲偄偆偒傢傔偰尩偟偄傕偺偱丄屆戙偺媄弍悈弨偐傜摫偒偩偟偨傕偺偱偡丅偟偐偟丄偙偺傛偆側尩偟偄忦審偱峫偊偰傕悢妛揑偵嬼慠惈偟偐弌偰偙側偄壜擻惈偑偁傞偺偱偡丅
丂擇偮偺嶳偐傜摍嫍棧偵偁傞屆暛偲偄偆働乕僗偱峫偊偰傒傑偡丅偁傞屆暛偵懳偟丄俙俛擇偮嶳偑摍嫍棧偵偁傞妋棫偼丄嶳俙偑屆暛偐傜嫍棧倶偱偁傞妋棪偲偦偺偲偒偵嶳俛偑偦傟偲摍嫍棧偱偁傞妋棪傪傕偲傔丄偦傟傪憤偰偺嫍棧偵傢偨偭偰懌偟偰偄偗偽媮傔傜傟傞偼偢偱偡丅崱丄屆暛偐傜敿宎倰埲撪偵偼嶳偼側偔丄傑偨敿宎俼傪椞堟偲偟偰峫偊傞偙偲偵偡傞丅偦偆偡偲傞丄嶳俙偑嫍棧倶忋偵偁傞妋棫偼丄
((x+嚈x)2-x2)兾/(R2-r2)兾偱媮傔傜傟丄嶳俛偑偦傟偲摍嫍棧偵偁傞妋棪偼丄岆嵎0.5亾埲撪偱偁傞偐傜丄嚈x偑旕忢偵彫偝偄偲偡傟偽丄
((x+0.005x)2-(x-0.005x)2)兾/(R2-r2)兾偲側傝傑偡丅偙偺擇偮傪妡偗崌傢偣傞偲丄嚈x2偼彫偝偡偓偰柍帇偱偒傞偺偱丄
2x丒嚈x丒0.02x2/(R2-r2)2偡側傢偪丄(0.04/(R2-r2)2)x3丒嚈x偲側傝傑偡丅偙傟傪憤偰偺倶偵偮偄偰偺榓傪媮傔傞偨傔偵偼愊暘偡傟偽傛偔丄
(0.01/(R2-r2)2)x4偲側傝傑偡丅偙傟傪倰偐傜俼傑偱偱寁嶼偡傞偲丄
(0.01/(R2-r2)2)(R4-r4)=0.01丒(R2+r2)/(R2-r2)偲側傝丄偙偺抣偑堦斣彫偝偄偺偼倰偑僛儘偺帪偱丄偦偺抣偼俼偵娭學側偔0.01偲偄偆偙偲偵側傝傑偡丅
丂廰扟栁堦巵偵傛傟偽丄戝榓嬤曈偺嫄戝屆暛偺懡偔偼丄媑栰媨丒捴堜戝捤屆暛丒榓愹墿嬥捤屆暛傪寢傇堦曈43.15km偺惓嶰妏宍撪偵廂傑傝偦偺悢偼34婎丄恾偵弌偰偄傞戝榓嬤曈偺嶳偺悢偼21偱偡丅偙偺嶳偺悢偼彮側偄偲巚偊傑偡偑丄偲傝偁偊偢偙偺悢偱峫偊傞偲丄屆暛偲擇偮偺嶳偺慻崌偣偼丄7140偲側傞丅偦傟偵懳偟丄34婎偺屆暛傪捀揰偲偟丄擇偮偺嶳傪掙曈偲偡傞擇摍曈嶰妏宍偼恾偱尒傞尷傝俆屄偺傒偱偡丅拞偵偼捁偺嶳屆暛傪拞怱偵摨怱墌忬偵俆偮偺嶳偑偁傞恾傕偁傝傑偢偐丄0.5亾埲撪偺婎弨傪枮偨偡偺偼偦偺偆偪偺堦慻偩偗偱偡丅妋棪0.01偲偄偆偙偲偼丄堦偮偺屆暛偵暯嬒俀偮偼擇摍曈嶰妏宍偑側偗傟偽側傜側偄偲偄偆偙偲偵側傝傑偡偐傜丄5屄偲偄偆悢帤偼嬌傔偰彮側偄屄悢偲偄偆偙偲偵側傞偱偟傚偆丅幚嵺丄傕偟杮摉偵俆屄偟偐側偐偭偨偲偡傟偽丄偦偺婋尟棪偼尷傝側偔100亾偵嬤偄偙偲偵側傝傑偡丅廰扟栁堦巵偑庢傝忋偘偰偄傞偺偼擇摍曈嶰妏宍偽偐傝偱側偔丄捈慄傗捈妏偲偄偭偨條乆側婔壗妛揑娭學偱偁傝丄偍偦傜偔偦傟傜偺娭學偑廳側傝偁偭偰栚偵偮偔傕偺偩偗傪庢傝忋偘丄懠偺傕偺偼斚嶨偵側傞偺偱婰偝側偐偭偨傕偺偲峫偊傜傟傑偡偑丄偟偐偟丄偦偺悢偵傛偭偰偼婋尟棪偑俆亾傪愗傜側偄応崌傕峫偊傜傟傞傢偗偱偡丅幚嵺丄昞寁嶼僜僼僩偱145屄傑偱寁嶼偟偨偲偙傠丄偦傟埲忋偼寁嶼晄壜擻偺婰崋偑弌偰寁嶼弌棃側偐偭偨偟丄偦傟偱傕婋尟棪偼傑偩82.7亾偱偡丅偙傟傑偱偺寁嶼偼悢妛揑偵尩枾側峫偊曽偵廬偭偨栿偱偼偁傝傑偣傫偑丄忦審揑偵偼偐側傝娒偔偟偨応崌傕偁傝丄尩枾偵寁嶼偟偨応崌偱傕丄婋尟棪傪俆亾埲撪偵廂傔傛偆偲偡傞偲丄屆戙偺媄弍悈弨傪偼傞偐偵挻偊偨惛搙偑昁梫偲偝傟傞偐傕偟傟側偄傢偗偱偡丅偪側傒偵丄慜婰偺寁嶼偱寁嶼偡傞偲丄婋尟棪俆亾埲撪偵廂傔傞偨傔偵偼丄嶳偺悢偑21偱嫍棧嵎0.014亾丄40偱0.0038亾偲側傝傑偡丅
丂曽埵慄偲偼偦偺擟堄偺揰偵偍偄偰丄搶惣慄偲嶌傞妏搙偑堦掕偺慄偺偙偲偱偡偐傜丄宱搙傪倄幉丄堒搙傪倃幉偲偟偰峫偊傞偲丄搶惣慄偵懳偟偰妏搙兤偺曽埵慄偼丂dy/dx=-1/tan兤丒1/cos
x丂偲偄偆偙偲偵側傝傑偡丅偙傟傪愊暘偡傞偲丂-1/tan兤丒log(tan(x/2+兾/4))+C丂偲側傝傑偡丅懳悢偼帺慠懳悢偱偡丅堒搙倝
丄宱搙倠偺揰傪捠傞曽埵慄偺俠偺抣偼丄k+1/tan兤丒log(tan(i/2+兾/4))偱丄偙傟偑偦偺曽埵慄偺愒摴偱偺宱搙偲偄偆偙偲偵側傝傑偡丅擇杮偺曽埵慄偺杒堒35搙偱偺暆偼丄愒摴偱偺宱搙嵎傪挿偝偵娨尦偟丄偦傟偵cos35亱傪妡偗丄偦偺暆偑彫偝偄傕偺傪懳徾偵偡傞応崌偼丄偝傜偵sin兤傪妡偗偨傕偺偲峫偊傞帠偑偱偒傑偡丅
丂堒搙宱搙偦傟偧傟(i1,k1)丄(i2,k2)傪捠傞曽埵慄偺妏搙兤偼丄
k1+1/tan兤丒log(tan(i1/2+兾/4))=k2+1/tan兤丒log(tan(i2/2+兾/4))偱梌偊傜傟丄
tan兤=(log(tan(i1/2+兾/4)-log(tan(i2/2+兾/4))/(k2-k1)偲側傝傑偡丅
丂傑偨丄俁揰俙俛俠偵偍偄偰丄俙俛丄俙俠丄俛俠偺偦傟偧傟偺妏嫍棧傪們丄倐丄倎丄佢俛俙俠傪俙偲偟傑偡偲丄
cos a=cos b丒cos c+sin b丒sin c 丒cos A偱偡偐傜丄cos A=(cos a-cos b丒cos
c)/(sin b丒sin c)偲側傝傑偡丅 堒搙宱搙偦傟偧傟(i1,k1)丄(i2,k2)偺擇揰偺妏嫍棧倎偼宱搙嵎傪
K偲偟傑偡偲丄cos a=cos(90-i1)丒cos(90-i2)+sin(90-i1)丒sin(90-i2)丒cos
K丂偑側傝偨偪傑偡丅側偍丄抧媴偺敿宎傪6371km偲偟偰寁嶼偟傑偟偨丅
丂丂
丂丂
丂