射影平面
２次元閉多様体の一種である射影平面は、メビウスの帯と円板を貼り合わせたものですが、ご存知のように、３次元空間の中では、
作ることが出来ません。しかし、４次元空間の中では、簡単に作ることが出来ます。
では、射影平面が４次元空間の中で作れることを、図を使って説明します。
４次元空間の座標軸を、x軸、y軸、z軸、w軸とします。
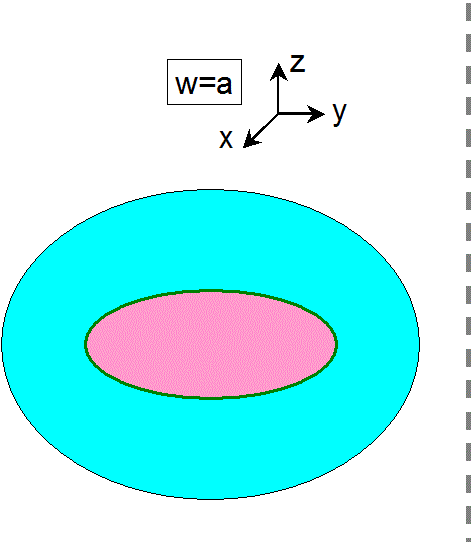
まず、w座標が a（w＝a）に固定された３次元空間の中に、一つの球面がある、とします。
ここで、一応、球面の表側を水色で表しておきます。
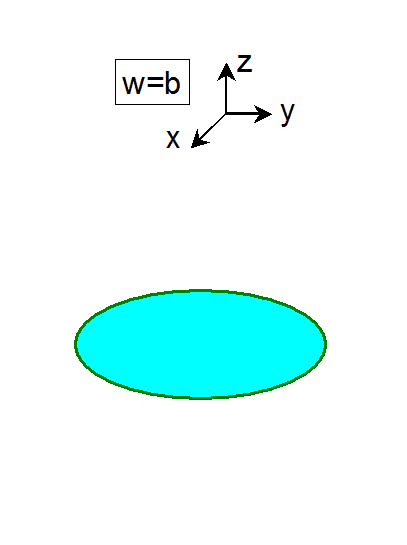
次に、球面から円板をくりぬき、その円板の w座標を aより少し大きい b（w＝b＞a）へ移動します。そうすると、w＝a での
３次元空間には、円板をくりぬいた球面だけが残ります。ここで、この円板をくりぬいた球面は、位相的には円板と同じもので
あることがわかります。すなわち、ここでの変形は、球面を２つの円板に分解して、片方の円板だけ w座標を少し移動したことに
なります。
なお、一応、わかり易くするために、円板をくりぬいた球面の裏側は、ピンク色で表しています。
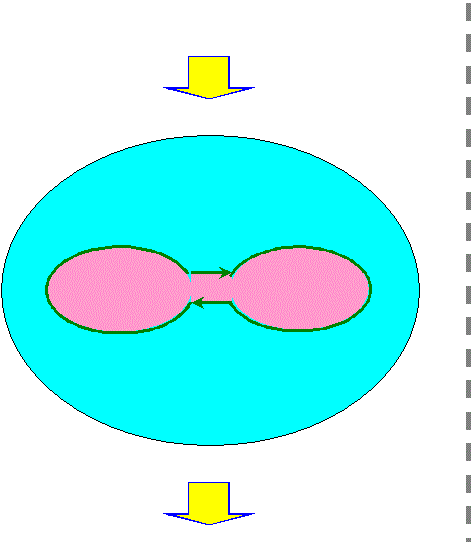
w＝a での円板をくりぬいた球面の境界線を変形して、図中の → の付いた２つの線分を → の向きに沿って貼り合せる
ことにします。
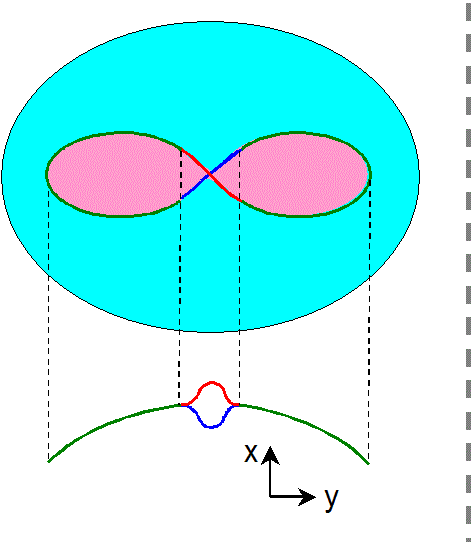
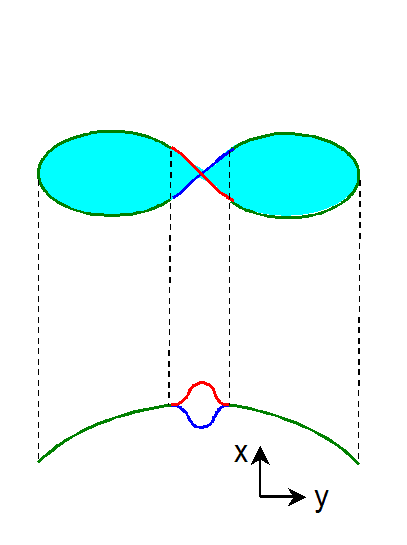
２つの線分の貼り合わせの結果、w＝a における円板をくりぬいた球面は、位相的には『円板』から『メビウスの帯』に
変化します。このメビウスの帯の境界線を辿って行くと、図のように、左側の緑色の線→赤色の線→右側の緑色の線→青色の線
→左側の緑色の線 となって一回りします。すなわち、この境界線は、位相的には円周と同じものです。
なお、参考までに、
このメビウスの帯の境界線を x−y座標系に投影したものも図示しておきました。
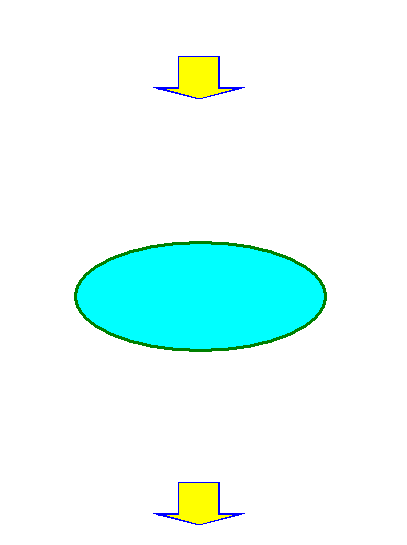
一方、w＝b にある円板では、その境界線は円周そのものです。したがって、図に示したように、この円板の境界線を w＝a に
おけるメビウスの帯の境界線と x−y−z座標上で一致するように、円板を変形することができます。
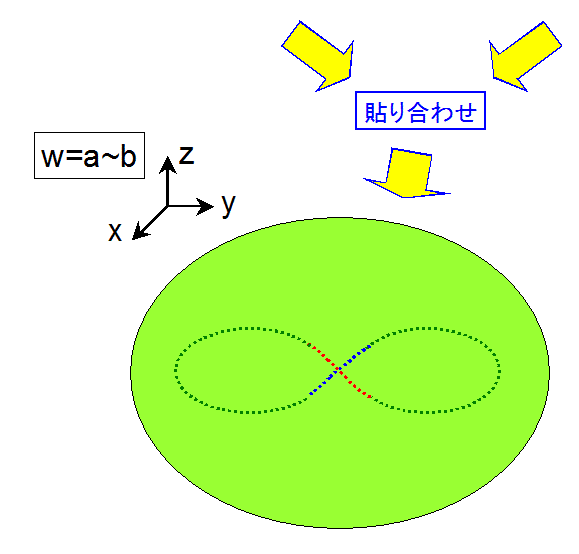
最後に、メビウスの帯と同じ境界線をもつ w＝b の変形円板について、その境界線が w＝a の位置に来るように境界線付近
の部分を連続的に変形します。その結果、w＝a において、メビウスの帯と変形円板の境界線どうしが貼り合わされます。すなわち、
射影平面が出来上がったことになります。
なお、射影平面は表面と裏面の区別のない２次元閉多様体なので、その点を考慮して、黄緑色で図示しました。
