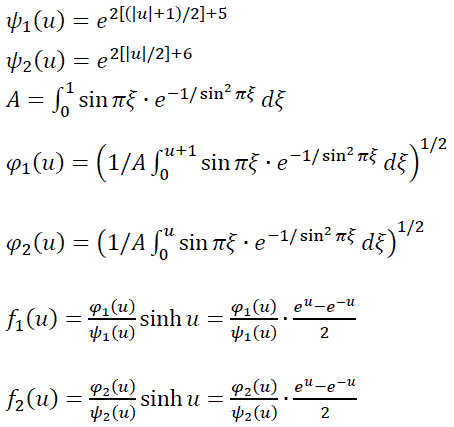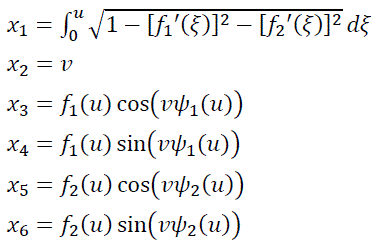定負曲率の二つ穴トーラス
「平坦トーラス」と同様、「定負曲率の二つ穴トーラス」について考えてみたいと思います。
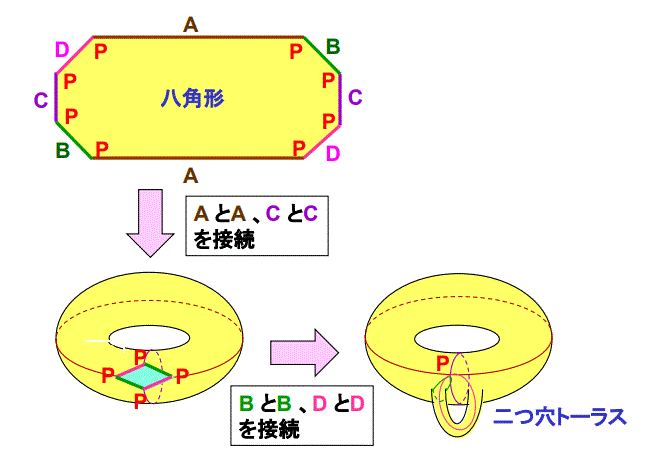
まず、右図のように、対向する辺の対Ａ、Ｂ、Ｃ、Ｄをもつ八角形を考えます。ＡとＡ、ＣとＣを接続すると、一つ穴トーラスから菱形（Ｂ、Ｄの
各２辺から成る菱形）を刳り抜いた曲面となります。つぎに、ＢとＢ、ＤとＤを接続すると、二つ穴トーラスが出来ます。なお、この過程で、八角形の
８つの頂点Ｐは一つにまとまり、二つ穴トーラス上の或る点Ｐとなります。また、以上の操作は、３次元ユークリッド空間内で行うことができます。
ところで、ホイットニーの埋め込み定理（Whitney embedding theorem）を用いると、任意のｍ次元可微分多様体（ｍ次元Ｃ１級多様体）は、
２ｍ次元ユークリッド空間の中に等長的に埋め込むことができます。よって、任意の２次元可微分多様体（２次元Ｃ１級多様体）は、４次元
ユークリッド空間の中に等長的に埋め込むことができます。また、１階導関数が連続なら、ガウス曲率が定義できるので、一定のガウス曲率をもつ様な
多様体は、可微分（Ｃ１級）多様体です。したがって、定負曲率の二つ穴トーラスは、４次元ユークリッド空間の中に等長的に埋め込むことが
できます。そして、このことを具体的に説明すると、以下の様になります。
まず、曲面上のあらゆる場所におけるガウス曲率が−１となる様な定負曲率曲面は、或る等角写像により、円板に射影することができます。これを
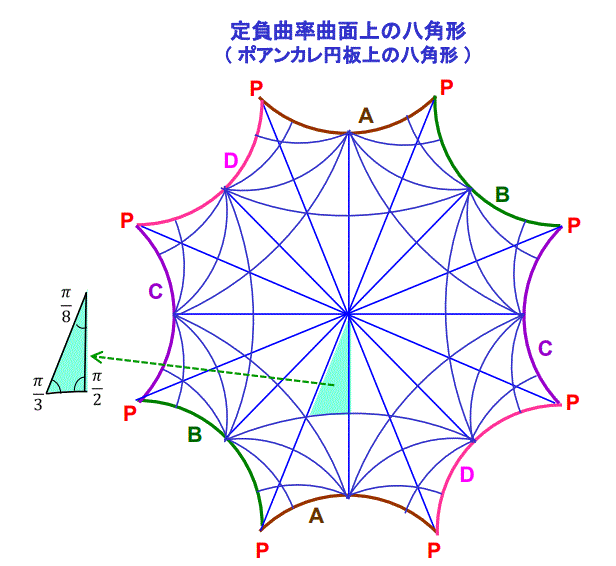
ポアンカレ円板模型（Poincare disk model）と呼びますが、右図の様なポアンカレ円板模型上の八角形を考え、対向する辺の対Ａ、Ｂ、Ｃ、Ｄを同一視すると、
閉じた定負曲率曲面となります。
なお、この八角形は、右図からわかる様に、π/8、π/3、π/2 を内角とする三角形９６個から構成でき、この様に９６個の三角形から成る定負曲率曲面の
ことを、ボルツァ面（Bolza Surface）と呼びます。ここで、π/8＋π/3＋π/2＝23π/24＜π となるので、この三角形は、定負曲率曲面上に存在するもの
であり、この三角形の各辺は、定負曲率曲面上の測地線（平面上の直線に相当）であることがわかります。
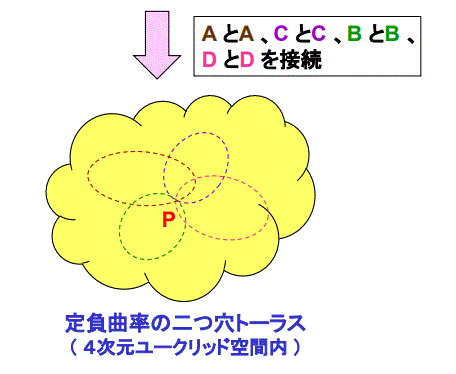
右上図の八角形において、定負曲率を保ちながら、ＡとＡ、ＣとＣ、ＢとＢ、ＤとＤを接続すると、定負曲率の二つ穴トーラスとなります。ここで、
この様な操作は、３次元ユークリッド空間内では実行できませんが、４次元ユークリッド空間内であれば、実行できます。すなわち、定負曲率の二つ穴
トーラスは、４次元（以上の）ユークリッド空間において実現できます。右図は、そのイメージ図です。右上図における八角形の８つの頂点Ｐは、右図に
おいては、一つにまとまり、定負曲率の二つ穴トーラス上の或る点Ｐになります。
以上の様に、定負曲率の二つ穴トーラスは、４次元ユークリッド空間内で実現することが出来ます。よって、４次元ユークリッド空間を表す４つの
座標軸 x, y, z, w を変数とする或る関数によって、定負曲率の二つ穴トーラスは表せそうな気がします。しかしながら、代数関数、三角関数、指数関数、
双曲線関数などの既知の関数を用いて、定負曲率の二つ穴トーラスを表すことは難しい様です。
参考資料： ・Wikipedia 『可微分多様体』、『Whitney embedding theorem』、『ガウス曲率』、
『ポワンカレの円板モデル』、『Bolza surface』
【 追記 】
ところで、定負曲率の二つ穴トーラスとは少し異なりますが、定負曲率の曲面（双曲面）であれば、６次元ユークリッド空間内で、既知の関数を用いて
実現することができます。具体的には、以下の通りです。
まず、例えば、u をパラメータとして、以下のように関数や定数を定義します。
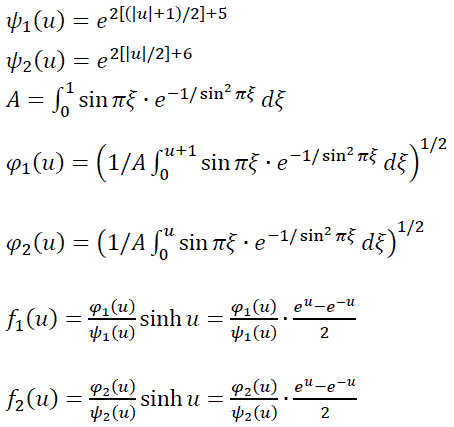
すると、以下の u と v をパラメータとする x i （i＝1〜6） で表される曲面は、ガウス曲率がどこでも
−１である定負曲率の曲面（双曲面）となります。
ここで、x i （i＝1〜6） は、６次元ユークリッド空間における互いに直交する６つの座標軸です。
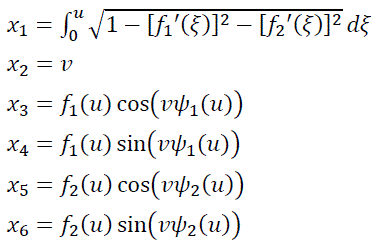
参考資料：・https://gdz.sub.uni-goettingen.de/id/PPN362162050_0059?tify={"pages":[225],"view":"info"}
