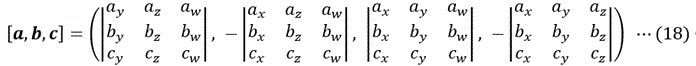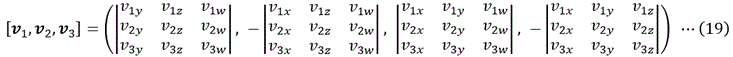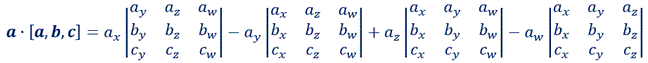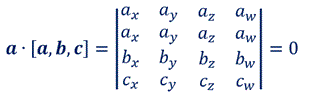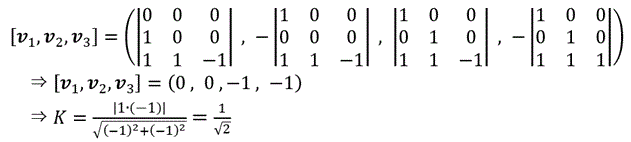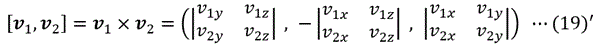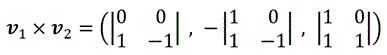4次元空間でねじれの位置にある平面と直線
x, y, z, w 直交座標系で表される4次元ユークリッド空間の内部に、平面Sと直線Tがあり、
SとTがねじれの位置の関係にあるとする。このとき、平面Sと直線Tの距離は、どのように
すれば求まるだろうか? 以下、その方法を示すことにする。
まず、平面Sは、ベクトル v1=(v1x, v1y, v1z, v1w)、
v2=(v2x, v2y, v2z, v2w)の張る平面であり、
点P(a, b, c, d)を含む平面であるとする。
また、直線Tは、ベクトル v3=(v3x, v3y, v3z, v3w)
の方向に延びる直線であり、点Q(e, f, g, h)を含む直線であるとする。
平面Sと直線Tがねじれの位置にあることから、ベクトル v1 、
v2 、v3 は1次独立であるから、
グラム・シュミットの直交化法により、互いに直交する3つの単位ベクトルの組 e1 、
e2 、e3 を、下記のようにして得ることができる。
なお、以下の各数式において、「 v・e 」は
2つのベクトル v 、e の内積を、「 |v| 」は
ベクトル v の絶対値(大きさ)をそれぞれ表すものとする。
e1=v1/|v1|
--- (1)
v2'=v2−(v2
・e1) e1 --- (2) ⇒
e2=v2'/|v2'|
--- (3)
v3'=v3−(v3
・e1) e1−(v3
・e2) e2 --- (4) ⇒
e3=v3'/|v3'|
--- (5)
つぎに、 e1 、e2 、
e3 とは1次独立になりそうなベクトル
v4=(v4x, v4y, v4z, v4w) を選び、再び、
グラム・シュミットの直交化法により、 e1 、e2 、
e3 のいずれとも直交する単位ベクトル e4 を、
下記のようにして求める。
v4'=v4−(v4
・e1) e1−(v4
・e2) e2−(v4
・e3) e3 --- (6) ⇒
e4=v4'/|v4'|
--- (7)
この e4 は、平面Sおよび直線Tと直交する向きに延びる単位ベクトルである。
すなわち、単位ベクトル e4 の方向はSからTへの最短経路の方向に等しい。
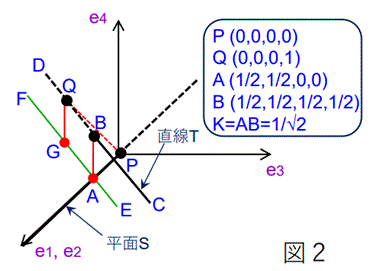
以上の内容を図示すると、図1のようになる。
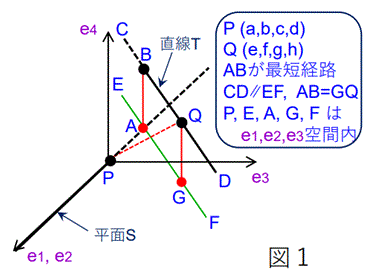
図1では、便宜上、e1 方向の軸と e2 方向の軸を1つに
まとめ、これと、e3 方向の軸、e4 方向の軸によって、
4次元ユークリッド空間を表している。よって、平面Sは、e1 ,
e2 軸となり、直線Tは、e1 ,
e2 , e3 軸が張る3次元空間(点P、E、A、G、F
を含む3次元空間)と平行に延びる直線(点C、B、Q、Dを通る直線)となる。(注1)
(注1)
ここで、図1について補足的説明をすると、図1に描かれている平面Sを表す直線(=e1 ,
e2 軸 )と直線EFは、ともに、e1 ,
e2 , e3 軸が張る3次元空間(ただし、
図1では平面として表されている)の中にある平面と直線を表している。よって、図1における平面Sを表す直線(=e1 ,
e2 軸 )は、平面Sのうち、直線EFの平面Sへの正射影を表す直線だけを抜き出して
描いていることになる。すなわち、平面Sの中で直線EFに最も接近する直線部分だけが、図1に表されている(そして、点Aは直線EFと平面Sの交点である)。
そもそも、SとTの距離などを求める上で必要なSの部分は、Sの中で直線EFに最も接近する直線部分だけで良い。よって、SとTの距離などを求めるためには、
図1のような表現は問題ない、と考えられる。
したがって、図1より、平面Sから直線Tまでの最短経路は
線分ABとなり、この長さがSとTの距離となる。ただし、図1より、AB=GQ であるから、SとTの距離は線分GQの長さと等しいことがわかる。
ここで、Pを始点とし、Qを終点とするベクトルを p とすると、図1からも明らかな様に、
p=(e-a, f-b, g-c, h-d)となる。したがって、平面Sと直線Tの距離を
Kとすると、Kは p の e4 方向への正射影の大きさ(=GQ)となる。
すなわち、K=|p・e4| --- (8)
( p と e4 の内積の絶対値)である。
なお、p は、明らかに e1 、e2 、
e3 とは1次独立であるから、v4=
p とすることができる。よって、(6)〜(8) の代わりに、
p'=p−(p
・e1) e1−(p
・e2) e2−(p
・e3) e3 --- (9) ⇒
K=|p'| --- (10) ,
e4=p'/|p'|
--- (11)
を用いることができる。すなわち、(10) より、e4 を求める前に、SとTの距離Kを求めることができる。
よって、 p の各成分がシンプルな場合には、(6)〜(8) ではなく (9)〜(10) を使って距離Kを求めた方が良さそうである。
前述したように、平面Sから直線Tまでの最短経路は、S上の点AからT上の点Bまでの線分である。それでは、AとBの座標は、どのようにすれば
求まるだろうか? 以下、その方法を示すことにする。
まず、点Pを始点とし、点Gを終点とするベクトルを q とすると、(9) より、
q=p−p'
=(p・e1) e1
+(p・e2) e2
+(p・e3) e3 --- (12)
である。また、直線EF上の任意の点をHとし、Gを始点、Hを終点とするベクトルを r とし、u を
任意の実数とすると、直線EFは直線Tと平行であるから、
r=u v3 --- (13)
と表すことができる。よって、Pを始点とし、Hを終点とするベクトルは q+r であり、
(12) 、(13) より、
q+r
=(p・e1) e1
+(p・e2) e2
+(p・e3) e3
+u v3 --- (14)
となる。さらに、Pを始点とし、Aを終点とするベクトルを s とすると、図1からわかる様に、
s は、q+r の一つであって、
e3 と直交するから、
s・e3
=(q+r)・e3=0 --- (15)
が成り立つ。よって、(14) 、(15) より、
s・e3
=(q+r)・e3
={ (p・e1) e1
+(p・e2) e2
+(p・e3) e3
+u v3 }・e3=0
⇒ p・e3
+u v3・e3=0
( ∵ e1・e3
=e2・e3=0 ,
e3・e3=1 )
⇒ u=−p・e3/
( v3・e3 )
=−p・e3/|v3'| --- (16)
( ∵ (4) , (5) より、v3・e3
=v3'・e3
=v3'・v3'/|v3'|
=|v3'| )
となる。したがって、(14) 、(16) より、
s=(p・e1 )
e1
+( p・e2 ) e2
+( p・e3 ) e3
−( p・e3/|v3'| )
v3 --- (17)
となる。すなわち、(17) より、s の各成分は求められる。よって、P(a, b, c, d)と (17) より、点Aの
座標は求められる。また、図1からわかる様に、点Aの座標と p' を表す (9) より、点Bの座標は求められる。
ところで、SとTの距離を求めるだけであれば、クロス積(ベクトル積)を用いる方法がある。一般に、4次元空間においては、3つのベクトル
a=(ax, ay, az, aw)、
b=(bx, by, bz, bw)、
c=(cx, cy, cz, cw)の
いずれとも直交するベクトルであるクロス積 [a,b,c] は、
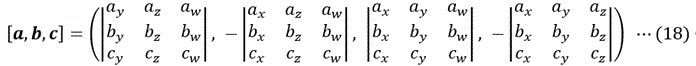
となる。(注2)
よって、3つのベクトル v1=(v1x, v1y, v1z, v1w)、
v2=(v2x, v2y, v2z, v2w)、
v3=(v3x, v3y, v3z, v3w)の全てと直交する
クロス積 [v1,v2,v3] は、
(18) より、
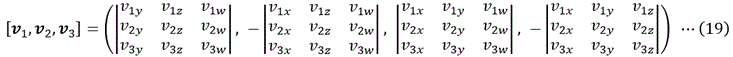
となり、前述の v4' を
[v1,v2,v3]
に置き換えることが出来るから、(19)、(7)、(8) より、SとTの距離 K は、次式により求められる。
K=|p・[v1,v2,v3]|
/|[v1,v2,v3]| --- (20)
(注2)
ベクトル a とクロス積 [a,b,c] の内積は、
(18) より、
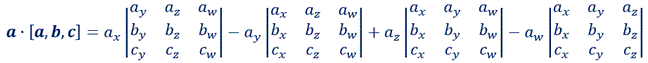
となるが、上式の右辺は、次の4次行列式の余因子展開に他ならないから、
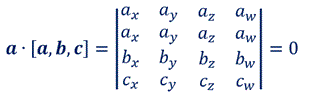
( ∵ 第1行=第2行より、行列式=0 )
となる。同様にして、b・[a,b,c]=0 、
c・[a,b,c]=0 も成り立つ。
よって、(18) で定義されたクロス積 [a,b,c] は、
ベクトル a 、b 、c のいずれとも直交していることがわかる。
以上の内容の具体的イメージを掴むため、簡単な例題と解答を作成したので、以下に示す。
【 例題1 】
4次元ユークリッド空間の内部に、点 P (0 ,0 ,0 ,0) を含み、ベクトル v1=(1, 0, 0, 0)、
v2=(0, 1, 0, 0)の張る平面Sと、点 Q (0, 0, 0, 1) を含み、
ベクトル v3=(1, 1, 1, -1)の方向に延びる直線Tが存在するとき、SとTの間の距離 K を
求めよ。また、SからTまでの最短経路の両端点をS上の点A、T上の点Bとしたとき、A、Bの座標を求めよ。
【 解答 】
前述の (1)〜(17) より、
e1=(1, 0, 0, 0), e2=(0, 1, 0, 0),
v3'=(1, 1, 1, -1)−(1, 0, 0, 0)−(0, 1, 0, 0)=(0, 0, 1, -1)
⇒ e3=(0, 0, 1/√2, -1/√2),
v4=p=(0, 0, 0, 1)
⇒ v4'=p'=(0, 0, 0, 1)−(-1/√2)(0, 0, 1/√2, -1/√2)
=(0, 0, 1/2, 1/2)
⇒ K=|p'|=√{(1/2)2+(1/2)2}=1/√2 ,
e4=p'/|p'|=(0, 0, 1/√2, 1/√2)
⇒ s=(0, 0, 0, 0)+(0, 0, 0, 0)−(1/√2)(0, 0, 1/√2, -1/√2)−(-1/√2)/√2(1, 1, 1, -1)
=(1/2, 1/2, 0, 0)
⇒ P(0, 0, 0, 0)+s=A(0+1/2, 0+1/2, 0+0, 0+0)=A(1/2, 1/2, 0, 0)
⇒ A(1/2, 1/2, 0, 0)+p'=B(1/2+0, 1/2+0, 0+1/2, 0+1/2)=B(1/2, 1/2, 1/2, 1/2)
となる。なお、K の別解として、前述の (19)〜(20) より、
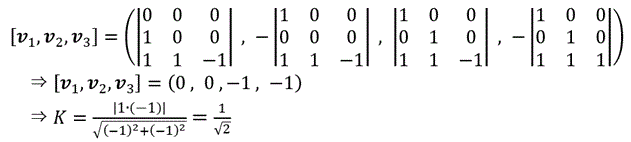
となる。
(答) K=1/√2 , A(1/2, 1/2, 0, 0), B(1/2, 1/2, 1/2, 1/2)
参考までに、上記の内容を図示すると、図2の様になる。
以上、4次元ユークリッド空間内での、ねじれの位置にある平面と直線の距離などを表す各数式を求めて来た。よって、容易にわかる様に、上記の各数式において、
次元を一つ下げることで、3次元ユークリッド空間内での、ねじれの位置にある2直線の距離などを表す各数式が導かれ、その結果は以下の様になる。
まず、x, y, z 直交座標系で表される3次元ユークリッド空間の内部に、図3のように、2つの直線S、Tがあり、SとTがねじれの位置の関係にあるとすると、
SからTまでの最短経路は線分ABとなり、この長さがSとTの距離となる。すなわち、直線Sは、ベクトル
v1=(v1x, v1y, v1z) の方向に延び、点P(a, b, c)を
含む直線であり、直線Tは、ベクトル v2=(v2x, v2y, v2z)
の方向に延び、点Q(e, f, g)を含む直線であるとすると、4次元の場合と同様、グラム・シュミットの直交化法により、
e1=v1/|v1|
--- (1)
v2'=v2−(v2
・e1) e1 --- (2) ⇒
e2=v2'/|v2'|
--- (3)
v3'=v3−(v3
・e1) e1−(v3
・e2) e2 --- (4) ⇒
e3=v3'/|v3'|
--- (5)
となり(ベクトル v3=(v3x, v3y, v3z)は、
e1 、e2 とは1次独立な任意のベクトル)、
e3 は SおよびTと直交し、SからTへの最短経路の方向に延びる単位ベクトルである。
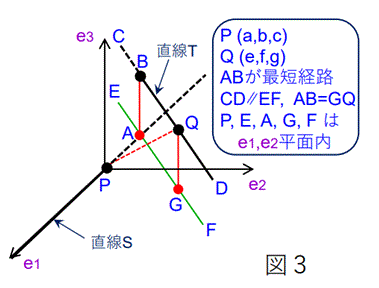
よって、Pを始点、Qを終点とするベクトルを p とすると、p=(e-a, f-b, g-c)となり、SとTの距離を
Kとすると、Kは p の e3 方向への正射影の大きさ、すなわち、
K=|p・e3| --- (8)'
( p と e3 の内積の絶対値)となる。
さらに、p は、e1 、e2
とは1次独立なので、v3=p とすることができ、(4)、(5)、(8)' の代わりに、
p'=p−(p
・e1) e1−(p
・e2) e2 --- (9)' ⇒
K=|p'| --- (10) ,
e3=p'/|p'|
--- (11)'
を使用できる。また、Pを始点、Gを終点とするベクトルを q とすると、(9)' より、
q=p−p'
=(p・e1) e1
+(p・e2) e2 --- (12)'
であり、Gを始点、直線EF上の任意の点Hを終点とするベクトルを r とすると、
r=u v3 --- (13)'( u は任意の実数)であり、Pを始点、Hを終点とするベクトル
q+r は、(12)' 、(13)' より、
q+r
=(p・e1) e1
+(p・e2) e2
+u v2 --- (14)'
となる。さらに、Pを始点、Aを終点とするベクトルを s とすると、
s と e2 は直交するから
s・e2
=(q+r)・e2=0 --- (15)'
となり、(14)' 、(15)' より、
s・e2
=(q+r)・e2
={ (p・e1) e1
+(p・e2) e2
+u v2 }・e2=0
⇒ p・e2
+u v2・e2=0
( ∵ e1・e2=0 ,
e2・e2=1 )
⇒ u=−p・e2/
( v2・e2 )
=−p・e2/|v2'| --- (16)'
( ∵ (2) , (3) より、v2・e2
=v2'・e2
=v2'・v2'/|v2'|
=|v2'| )
となる。よって、(14)' 、(16)' より、
s=(p・e1 )
e1
+( p・e2 ) e2
−( p・e2/|v2'| )
v2 --- (17)'
となる。すなわち、(17)' より、s の各成分は求められ、P(a, b, c)と (17)' より、点Aの座標は求められる。また、点Aの座標と
p' を表す (9)' より、点Bの座標は求められる。
また、クロス積(ベクトル積)を用いる場合、(19) の3次元版が
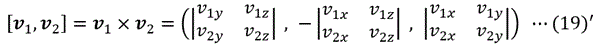
となり、v3' を v1×v2
に置き換えることが出来るから、(19)' 、(5) 、(8)' より、K は、次式により求められる。
K=|p・(v1×v2)|/
|v1×v2| --- (20)'
最後に、例題1と同様に、簡単な例題と解答を作成したので、以下に示す。
【 例題2 】
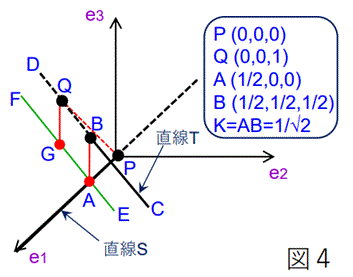
3次元ユークリッド空間の内部に、点 P (0 ,0 ,0) を含み、ベクトル v1=(1, 0, 0)の方向に延びる直線Sと、
点 Q (0, 0, 1) を含み、ベクトル v2=(1, 1, -1)の方向に延びる直線Tが存在するとき、SとTの間の距離 K を
求めよ。また、SからTまでの最短経路の両端点をS上の点A、T上の点Bとしたとき、A、Bの座標を求めよ。
【 解答 】
前述の (1)〜(17)' より、
e1=(1, 0, 0),
v2'=(1, 1, -1)−1(1, 0, 0)=(0, 1, -1)
⇒ e2=(0, 1/√2, -1/√2),
v3=p=(0, 0, 1)
⇒ v3'=p'=(0, 0, 1)−(-1/√2)(0, 1/√2, -1/√2)=(0, 1/2, 1/2)
⇒ K=|p'|=√{(1/2)2+(1/2)2}=1/√2 ,
e3=p'/|p'|=(0, 1/√2, 1/√2)
⇒ s=(0, 0, 0)−(1/√2)(0, 1/√2, -1/√2)−(-1/√2)/√2(1, 1, -1)=(1/2, 0, 0)
⇒ P(0, 0, 0)+s=A(0+1/2, 0+0, 0+0)=A(1/2, 0, 0)
⇒ A(1/2, 0, 0)+p'=B(1/2+0, 0+1/2, 0+1/2)=B(1/2, 1/2, 1/2)
となる。なお、K の別解として、前述の (19)'〜(20)' より、
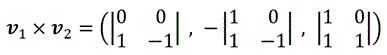
⇒ v1×v2=(0, 1, 1)
⇒ K=|1・1|/√(12+12)=1/√2
となる。
(答) K=1/√2 , A(1/2, 0, 0), B(1/2, 1/2, 1/2)
参考までに、上記の内容を図示すると、図4の様になる。
参考資料:
・Wikipedia 『グラム・シュミットの正規直交化法』、『クロス積』
・下記URL
https://risalc.info/src/distance-between-two-lines.html( 直線と直線の距離を与える公式と最近点 - 理数アラカルト - )