

暗号理論の応用を試みた行列変換のあれこれ。そのレポートです。
Top Page へ
Contents
| ◎ 暗号化と変換 | |
| ◎ ASCII 表の変換 | |
| ◎ 行列変換の利用 | |
| ◎ 行列次元と非正則の関係 | |
| ◎ 逆行列変換の問題と実際 | |
| ◎ プログラム改良で起きる問題 | |
| ◎ 文献 | |
| 暗号化方法 | 暗号鍵 | 変換 |
| 手続き | キーワード、暗号表、素数を使う | 決められた操作で変換する |
| 特徴 | 暗号鍵が不明な場合、解読が困難。 暗号鍵の安全記憶が必要。 | 変換操作が解読されやすい。 平文の情報だけで変換可能。 |
| 可逆性 | ほぼ可能 | 不可能な場合も多い |
| 代表例 | ナンバー錠、パスワード、公開鍵暗号方式 | シーザー暗号、行列変換 |
| 文字 | 16進数 | 10進数 |
| 0〜9 | 0x30 - 0x39 | 48 - 57 |
| A〜Z | 0x41 - 0x5A | 65 - 90 |
| a〜z | 0x61 - 0x7A | 97 -122 |
 行列変換主体の暗号化フローチャート(案)
行列変換主体の暗号化フローチャート(案)
| 要素の上限値 n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | 20 | 50 | 100 |
| det=0 の個数 | 1 | 6 | 15 | 32 | 49 | 86 | 111 | 160 | 209 | 278 | 703 | 1360 | 10950 | 52160 |
| 非正則の割合(%) | 100 | 37.5 | 18.5 | 12.5 | 7.84 | 6.64 | 4.62 | 3.91 | 3.19 | 2.78 | 1.39 | 0.85 | 0.175 | 0.052 |
| 要素の上限値 n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| det=0 の個数 | 1 | 248 | 3975 | 29104 | 119405 | 436818 | 1105537 | 2790818 | ||
| 非正則の割合(%) | 100 | 48.4 | 20.2 | 11.1 | 6.11 | 4.33 | 2.74 | 2.08 | ||
| 計算時間[s] | 5 | 25 | 97 | 5m20s | ||||||
| 要素の上限値 n | 1 | 2 | 3 | |
| det=0 の個数 | 1 | 33472 | 7382001 | |
| 非正則の割合(%) | 100 | 51.1 | 17.1 | |
| 計算時間[s] | 1 | 6m56s |
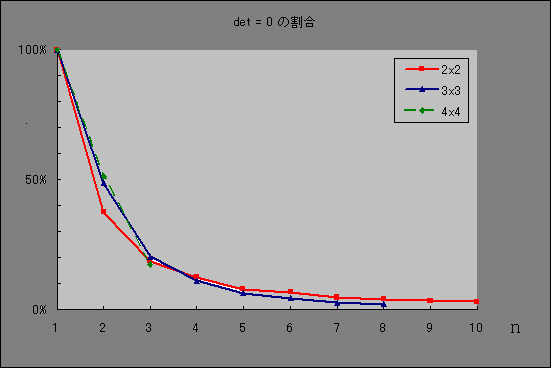 話を戻すと、今回のプログラムでは、ASCII コードの48〜122 が
範囲であり、平文を正方行列にした場合に行列次元は3〜10程度なので、
非正則の割合は1%未満と推定して良いでしょう。これぐらいなら非正則の
場合は省略しても良さそうです。
計算プログラム(C言語)
話を戻すと、今回のプログラムでは、ASCII コードの48〜122 が
範囲であり、平文を正方行列にした場合に行列次元は3〜10程度なので、
非正則の割合は1%未満と推定して良いでしょう。これぐらいなら非正則の
場合は省略しても良さそうです。
計算プログラム(C言語)
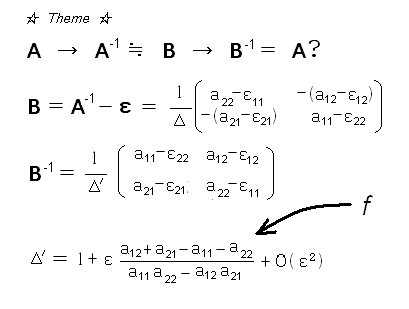 実際は式のように、n=100 の場合、切捨てた小数εは小数点2桁以降なら
(1-0.09)/(1+0.09f)のように整数値へ四捨五入が可能ですが、f は最大でも
100 の位ですので、小数点4桁以降の切捨てなら再変換が問題なくできそうです。
実際は式のように、n=100 の場合、切捨てた小数εは小数点2桁以降なら
(1-0.09)/(1+0.09f)のように整数値へ四捨五入が可能ですが、f は最大でも
100 の位ですので、小数点4桁以降の切捨てなら再変換が問題なくできそうです。
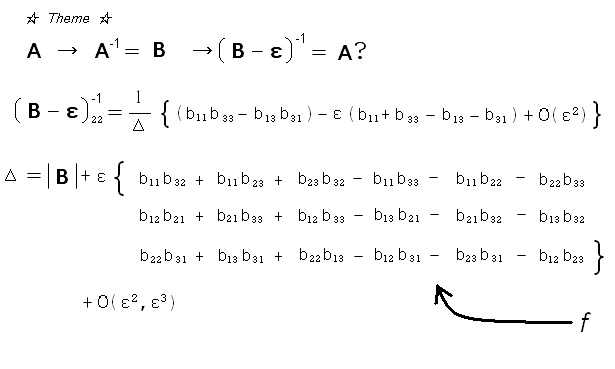 3x3 については、掃きだし法で丁寧に計算を続けていくと、
要素(2,2) では分子の方は、小数点2桁に抑えるために
εは小数点4桁になります。これに対して分母の方は、
最大で 105 弱の可能性もあるので、εは小数点7桁なら安全です。
しかし符号を見ると係数 f が打ち消しあいそうなので、
分子に合わせて小数点4桁ぐらいでもよさそうです。
他の要素も対称性から同じオーダーになるでしょう。
3x3 については、掃きだし法で丁寧に計算を続けていくと、
要素(2,2) では分子の方は、小数点2桁に抑えるために
εは小数点4桁になります。これに対して分母の方は、
最大で 105 弱の可能性もあるので、εは小数点7桁なら安全です。
しかし符号を見ると係数 f が打ち消しあいそうなので、
分子に合わせて小数点4桁ぐらいでもよさそうです。
他の要素も対称性から同じオーダーになるでしょう。
