= 0apx.322. 線形計画シンプレックス表 (3.2.2 例題) 目次（第5章）へ
［解］ ｘ1 =ｘ2 =ｘ3 =ｘ4 = 0とすると，初期解として，ｘ5 = 30，ｘ6 = 12，ｘ7 = 18，ｘ8 = 0 が得られ，
シンプレックス表（ステップ- 1）
|
ｃj |
|
0 |
0 |
-1 |
-1 |
0 |
0 |
0 |
M |
|
|
ｃi |
P 0 |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
|
|
P 5 0 |
30 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
① |
|
P 6 0 |
12 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
② |
|
P 7 0 |
18 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
③ |
|
P 8 M |
0 |
1* |
1 |
- 0.1 |
-0.1 |
0 |
0 |
0 |
1 |
④ |
|
z j |
0 |
M |
M |
- 0.1M |
-0.1M |
0 |
0 |
0 |
M |
|
|
z j－c j |
|
M |
M |
1-0.1M |
1-0.1M |
0 |
0 |
0 |
0 |
|
|
|
|
↑ |
|
|
|
|
|
|
|
|
= 0
から *印をピボットとして，Ｐ8 ベクトルをＰ1ベクトルに入れかえる．(ｌ= 4，ｋ= 1，ｉ= 1，2，3 )，ｂ
t´= ｂ
4´=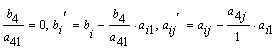 
からつぎの表が得られる．
シンプレックス表（ステップ- 2）
|
ｃ j |
|
0 |
0 |
-1 |
-1 |
0 |
0 |
0 |
M |
|
|
|
ｃ i |
P 0 |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
|
|
|
P 5 0 |
30 |
0 |
-1 |
0.1 |
0.1 |
1 |
0 |
0 |
- 1 |
①′ |
①－④ |
|
P 6 0 |
12 |
0 |
1 |
1* |
0 |
0 |
1 |
0 |
0 |
②′ |
② |
|
P 7 0 |
18 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
③′ |
③ |
|
P 1 0 |
0 |
1 |
1 |
- 0.1 |
- 0.1 |
0 |
0 |
0 |
1 |
④′ |
④ |
|
z j |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
z j - c j |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
↑ |
|
|
|
|
|
|
|
シンプレックス表（ステップ- 3）
|
ｃ j |
|
0 |
0 |
-1 |
-1 |
0 |
0 |
0 |
M |
|
|
|
ｃ i |
P 0 |
P 1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
|
|
|
P 5 0 |
28.8 |
0 |
-1.1 |
0 |
0.1 |
1 |
- 0.1 |
0 |
-1 |
①″ |
①′- 0.1②′ |
|
P 3 -1 |
12.0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
②″ |
②′ |
|
P 7 0 |
18.0 |
0 |
0 |
0 |
1* |
0 |
0 |
1 |
0 |
③″ |
③′ |
|
P 1 0 |
1.2 |
1 |
1.1 |
0 |
-0.1 |
0 |
0.1 |
0 |
1 |
④″ |
④′+ 0.1②′ |
|
z j |
-12.0 |
0 |
- 1 |
-1 |
0 |
0 |
- 1 |
0 |
0 |
|
|
|
z j - c j |
0 |
0 |
- 1 |
0 |
1 |
|
- 1 |
0 |
- M |
|
|
|
|
|
|
|
|
↑ |
|
|
|
|
|
|
=18
シンプレックス表（ステップ- 4）
|
ｃj |
|
0 |
0 |
-1 |
-1 |
0 |
0 |
0 |
M |
|
|
ｃi |
P 0 |
P1 |
P 2 |
P 3 |
P 4 |
P 5 |
P 6 |
P 7 |
P 8 |
|
|
P5 0 |
27.0 |
0 |
- 1.1 |
0 |
0 |
1 |
- 0.1 |
- 0.1 |
- 1 |
①″- 0.1③″ |
|
P3 - 1 |
12 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
②″ |
|
P4 - 1 |
18 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
③″ |
|
P1 0 |
3.0 |
1 |
- 1.1 |
0 |
0 |
0 |
0.1 |
0.1 |
1 |
④″+ 0.1③″ |
|
z j |
30 |
0 |
- 1 |
- 1 |
- 1 |
0 |
- 1 |
- 1 |
0 |
|
|
z j－c j |
|
0 |
1 |
0 |
0 |
0 |
- 1 |
- 1 |
- M |
|
ここで，すべてのｚ j－ｃ
j は0または負になり，最適解ｘ1 =3.0，ｘ3 = 12，ｘ4 = 18，ｘ5＝27.0，ｘ2 ＝ｘ6＝ｘ7＝ｘ8＝
0で，目的関数ｚ＝ - 30である． 
また，ｘ2 ，ｘ6 ，ｘ7の潜在価格は - 1であり，期間Ｓ11，Ｓ20 を１時間増加するとｚは１だけ増加することを示している．